Механіка

Дослід Архімеда з короною

Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания корона оказалась соответствующей выданному весу золота.

После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».

Затем, исходя из своего открытия, он, говорят, сделал два слитка, каждый такого же веса, какого была корона, один из золота, другой из серебра. Сделав это, он наполнил сосуд до самых краев и опустил в него серебряный слиток, и... соответственное ему количество воды вытекло. Вынув слиток, он долил в сосуд такое же количество воды.., отмеряя вливаемую воду секстарием (0,547л), чтобы, как прежде, сосуд был наполнен водой до самых краев. Так он нашел, какой вес серебра соответствует какому определенному объему воды.

Произведя такое исследование, он таким же образом опустил золотой слиток... и, добавив той же меркой вылившееся количество воды, нашел на основании меньшего количества секстантов воды (секстант – римская мера веса, равная 0,534 Н), насколько меньший объем занимает слиток».

Потом тем же методом был определен объем короны. Она вытеснила воды больше, чем золотой слиток, и кража была доказана.

Часто этот, рассказ связывают с открытием закона Архимеда, хотя он касается способа определения объема тел неправильной формы.

Дослід Торрічеллі

Дата: 1643.

Методы: качественное и количественное исследование.

Прямота эксперимента: прямое наблюдение; изменение условий эксперимента с целью выделить механизм, приводящий к наблюдаемому явлению.

Искусственность изучаемых условий: естественные.

Исследуемые фундаментальные принципы: основной закон гидростатики, наличие атмосферного давления.

С воим достаточно простым Опытом Эвангелиста Торричелли (1608–1647) измерил атмосферное давление и сделал первые выводы о давлении столба жидкости, которые зафиксированы в основном законе гидростатики. В опыте, поставленном в 1643 г. использовалась запаянная с одного конца тонкая стеклянная трубка, которую наполняли ртутью, после чего переворачивали и открытым концом опускали в стеклянную ванночку, также наполненную ртутью (см. рис.). В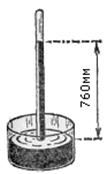 случае воды мы знаем, что обычно в подобном случае в трубку должны начать поступать пузыри воздуха, а сама жидкость начнет выливаться. В опыте же Торричелли трубка была сделана достаточно тонкой и хорошо прилегала ко дну корытца, так что воздух в нее не проходил. Вместо этого только часть ртути перетекала в корытце, а у запаянного конца трубки возникала т.н. пустота Торричелли (на самом деле, эта «пустота» была наполнена насыщенными парами ртути, но их давление при комнатной температуре гораздо меньше атмосферного, поэтому приближенно можно назвать эту область пустотой).

Наблюдаемый эффект свидетельствовал о том, что ртуть от полного выливания удерживала некоторая сила, действующая со стороны нижнего конца трубки. Эта силу и создавало атмосферное давление, противостоящее весу столба жидкости. С точки зрения современных представлений,

где    — атмосферное давление,    — давление насыщенных паров ртути в пустоте Торричелли,    — высота столба ртути,    — плотность ртути,    — ускорение свободного падения.

Столб ртути в трубке имел всегда одну и ту же высоту, равную примерно 760мм. Отсюда и единица измерения давления — миллиметр ртутного столба (мм рт. ст.). По формуле выше мы получаем, что в Паскалях

Другое интересное свойство столба состояло в том, что он имел ту же высоту и в наклоненной к вертикали трубке (см. рис.). Более того, в принципе, можно было сделать и S-образную трубку — и все равно ртуть в ней держалась бы на той же отметке в 760 мм. В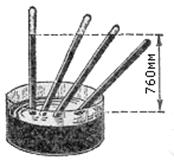 ыходит, что давление, создаваемое столбом ртути, которое и уравновешивается атмосферным давлением, зависит только от высоты столба. Кроме того, наблюдая картину, изображенную на последнем рисунке, Торричелли сделал вывод о том, что ртуть от полного вытекания в ванночку удерживает не таинственная сила всасвывания со стороны образовавшейся в верху трубки пустоты, а именно сила атмосферного давления снизу. Действительно, в первом случае эта сила должна была бы меняться при наклоне трубки, поскольку объем пустоты Торричелли при этом также менялся. Также использовалась одна ванночка со вставленными в нее трубками разной длины, в которых, соответственно, и пустоты Торричелли имели различные объемы.

Наконец, Торричелли заметил, что высота столба ртути в трубке менялась со временем, в частности, в течение суток. Это тоже говорило о внешней причине удержания ртути в трубке и послужило первым выполненным Торричелли барометрическим наблюдением. С этого открытия начались многочисленные исследования взаимосвязи погодных явлений и атмосферного давления.

Стоит отметить, что первые наблюдения атмосферного давления были описаны еще учителем Торричелли Галилео Галилеем в труде «Беседы». Там он цитировал итальянских колодезников, которые стали использовать насосы для откачивания воды из глубины колодца. Они заметили, что таким способом удается поднять воду с глубины не более 10 метров, каким бы хорошим ни был насос. Исходя из этого замечания, Галилей оценил «боязнь пустоты» (атмосферное давление)  величиной порядка одного килограмма на квадратный сантиметр. Эта достаточно хорошая оценка никоим образом не обесценивает вклад Торричелли в данные исследования, показавшего, что «боязнь пустоты» связана не с самой пустотой, а с весом воздуха, давящего сверху на нас, живущих на дне воздушного океана.

Несмотря на последовательность исследований Торричелли вера в воздух как чисто духовное начало и в всасывающую силу пустоты была разрушена даже после его смерти. Лишь опыты Паскаля, построившего водяной барометр и показавшего, что давление воздуха зависит от высоты, а также знаменитый опыт Отто фон Герике с Магдебургскими полушариями (см. рис. ниже) начали стирать из умов ученых старые взгляды. Ниже представлена знаменитый рисунок Г. Шотта, на котором изображены 16 лошадей, по 8 с каждой стороны от металлических Магдебургских полушарий, между которыми создан вакуум. Полушария прижимает друг к другу не что иное как атмосферное давление, и эта сила столь велика, что оторвать полушария друг от друга не может даже такая приличная упряжь.

Дослід Б. Паскаля

Дата: 1647–1653.

Методы: качественное и полуколичественное исследование.

Прямота эксперимента: прямое наблюдение.

Искусственность изучаемых условий: естественные и искусственные.

Исследуемые фундаментальные принципы: основной закон гидростатики.

Ф ранцузский ученый Блез Паскаль (1623–1662) прославился и в математике, и в физике, и философии — матери всех наук. Один из важнейших его вкладов в физику связан с изучением гидростатики, т.е. науки о жидкости (газе) в состоянии равновесия (т.е. покоя).

Опыт Паскаля является притчей во языцех в физике: наверное, каждому покажется знакомой гравюра, изображенная ниже. На ней Паскаль, стоя на балконе второго этажа своего дома, наливает в тонкую длинную трубку, вставленную в бочку с водой, пару кружек воды — и бочка трескается, не выдерживая давления большого столба жидкости. Опыт наглядно демонстрирует гидростатический парадокс: сила давления жидкости на дно сосуда оказывается гораздо большей, чем вес этой жидкости.

Итак, по указанию Паскаля дубовую бочку до краев наполнили водой и герметично закрыли. После этого в верхней ее крышке проделали отверстие и вставили в него тонкую длинную трубку, так, чтобы последняя располагалась вертикально. После того, как эту трубку заполнит вода, долитая Паскалем из кружки, давление в бочке увеличится на величину

где   — плотность воды,   — ускорение свободного падения, а   — высота трубки. Если подставить последнее значение в формулу для давления, то мы получаем  . Такого избыточного давления, действующего изнутри бочки наружу, как оказывается, вполне достаточно, чтобы сломать крепкое дерево.

Заметим, во-первых, что еще большая сила атмосферного давления давит на бочку, когда последняя открыта и в нее не вставлена тонкая трубка — но эта сила давит как на внешнюю, так и на внутреннюю поверхность стенок бочки. Таким образом, атмосферное давление только сжимает деревянные стенки. Если бы последние были хрупкими по отношению к сжатию, то бочка не выдержала бы и простого атмосферного давления. Во-вторых, если принять диаметр бочки   равным одному метру, то получается, что на ее дно давит сила, равная

что соответствует весу твердого тела с массой порядка трех тонн. Сама формула для гидростатического давления (см. выше) является выражением закона Паскаля. Однако этот закон также утверждает, что давление внутри покоящейся жидкости одинаково во всех направлениях. В частности, вода давит на самые нижние части боковых стенок бочки Паскаля с той же силой (на единицу площади), что и на ее дно. В независимости давления от направления Паскаль убедился с помощью другого опыта, а именно опыта с трубкой, названной впоследствии в его честь (см. рис. справа). Т рубка Паскаля состоит из цилиндрического стеклянного сосуда, в который вставлен поршень, и полого шара с маленькими отверстиями, надетого на конец сосуда. Если трубку заполнить водой (см. правую трубку на рис.) и надавить на поршень, то из отверстий в шаре польются водяные струйки. По мощности этих струек (а также их средней длине их прямолинейных участков) можно судить о давлении, с которым вода выбрасывается сквозь данное отверстие в шаре. Поскольку эти струйки имеют примерно одинаковые параметры, можно заключить, что давление в жидкости передается равномерно по всем направлениям. Аналогичный опыт проводился с дымом (см. левую трубку на рис.), что позволило заключить, что закон Паскаля справедлив и для газов. Естественно, форму струек искажает гравитационное поле Земли — но повернув трубку вверх ногами, мы увидим, что, несмотря на то, что теперь поршень находится снизу от шара, наблюдается все та же картина: струйки, бьющие вверх, «закругляются» чуть быстрее струек, бьющих вниз. Это говорит о том, что различие в их длине вызвано, в основном, притяжением Земли.

Наконец, формула для гидростатического давления, приведенная в начале данной статьи, заставляет сделать предположение, что атмосферное давление уменьшается с высотой, причем примерно линейно. В этом Паскаль также убедился с использованием ртутного барометра Торричелли, проведя опыты в Париже на башне Сен-Жак, а также сверив их результаты с результатами опытов, проведенных по зятем Флореном Перье у горы Пюи-де-Дом. В честь этих экспериментов на башне Сен-Жак впоследствии был установлен памятник Паскалю.

Т акже несложный опыт (см. рис. справа) позволяет убедиться в том, что давление жидкости убывает линейно с высотой. В цилиндр, в боковых стенках которого на различной высоте проделаны маленькие отверстия, наливают воду — и, так же, как и в опыте с трубкой Паскаля, наблюдают длины струек из этих отверстий. Как нетрудно увидеть, струя тем сильнее, чем ниже расположено отверстие, что свидетельствует о повышении гидростатического давления под весом столба жидкости.

Помимо своих теоретических выводов, опыты Паскаля и его основной закон гидростатики привели к изобретению им г идравлического пресса (см. рис. справа), который повсеместно используется в современной технике. Если поршни, как на рисунке, находятся на одной высоте, то давление жидкости под ними одинаково и равно  . Поршни можно уравновесить, если положить на них грузы массами   и  , соответственно, чтобы силы тяжести, действующие на эти грузы, уравновешивались силой давления жидкости (см. рис.):

Этот же принцип позволяет с помощью малой силы  , приложенной к меньшему поршню, создавать силу  , превышающую   и действующую на больший, что активно и используется в технике.

Опыты Паскаля по давлению жидкостей и газов еще раз развенчали восходящую к Аристотелю теорию о «боязни пустоты», которой, в частности, объясняли удержание столбика ртути в трубке барометра Торричелли. Паскаль показал, что подобные явления являются следствием давления, а не обратной силы, силы всасывания, действующей со стороны пустоты, а также что все физические явления встают на свои места, если только принять во внимание давление окружающего нас воздуха.

Наконец, сформулированный на основе опытов Паскаля основной закон гидростатики (закон Паскаля) имеет фундаментальное значение для гидростатики и выражает собой изотропность (независимость от направления) внутренних напряжений, возникающих в жидкостях и газах.

Г. Галілея

Дата: 1589 (падение тел), 1638 (наклонная плоскость).

Методы: построение математической модели, мысленный эксперимент изучение наблюдаемых явлений с количественной стороны.

Прямота: непосредственное измерение.

Искусственность изучаемых условий: условия, близкие к естественным (земным).

Исследуемые фундаментальные принципы: основной закон механики Ньютона (в упрощенной форме).

Г алилео Галилей (1564–1642) не зря удостоился чести быть названным первым в истории физиком самим Ричардом Фейнманом — нобелевским лауреатом, одним из отцов квантовой электродинамики. Пожалуй, до него мало кто набирался необходимой смелости, чтобы взобраться на Пизанскую башню (высота — 56,7 м, что сравнимо с современным 18-этажным домом), прихватив с собой 80-килограммовое пушечное ядро — всего лишь для того, чтобы отправить последнее в стремительное падение на головы зевак.

Еще в студенческие годы Галилей начал сомневаться в справедливости положений Аристотеля, согласно которым тяжелое тело должно было падать быстрее легкого. Более того, древнегреческий философ полагал, что скорость тел, брошенных с одной высоты, в точке падения на землю будет пропорциональна их массам. Для опровержения первого положения своего великого предшественника Галилео Галилей использовал его же метод, т.е. метод логических рассуждений:

«Представим себе два тела, одно легкое, а другое — более тяжелое — соединенные между собой с помощью цепи. Сбросим эту систему тел с вершины башни. Если предположить, что более тяжелые тела действительно падают быстрее более легких тел, цепь вскоре натянется, поскольку легкое тело будет падать с запозданием, по сравнением с более тяжелым (и, следовательно, замедлять движение последнего — прим. ред.). В то же время, система, рассматриваемая в целом, тяжелее, чем более тяжелое тело, р ассматриваемое по одиночке, и, следовательно, должна падать быстрее последнего. Это противоречие позволяет нам сделать заключение о несправедливости нашего предположения.»

Данный мысленный эксперимент и подтвердили опыты, проведенные на Пизанской башне в 1589 г. (см. рис. справа). Галилей сбрасывал с Пизанской башни пушечное ядро весом 80 кг и мушкетную пулю массой порядка 200 г. Выбором тел сферической формы Галилей рассчитывал уменьшить влияние сопротивления воздуха на их падение.

 

Несмотря на важность эксперимента Галилея, нельзя утверждать, что в нем была подтверждена точка зрения Галилея относительно падения тел в поле силы тяжести. Скорее, была опровергнута физика Аристотеля. Действительно, несложные вычисления показывают, что мушкетная пуля должна упасть на землю более чем на четверть секунды позже ядра — при том, что само падение должно было длиться всего-то 3–4 секунды. Более того, между пулей и ядром в момент достижения земли последним должно быть расстояние порядка 6 метров. Это расстояние сложно было не заметить тем, кто стоял у подножия башни. Поэтому остается уповать на тот факт, что по аристотелевской теории это расстояние должно было быть гораздо большим.

Подтвердив качественно свою догадку о независимости скорости падения тела от его массы, Галилей решил исследовать падение тел количественно. Однако в его время не было приборов, позволявших измерять малые промежутки времени с хорошей точностью, поэтому исследовать падение напрямую не оставляло никаких перспектив. И тут голову великого ученого осенила мысль: а почему бы не заменить стремительное падение более медленным движением, но которое должно было бы обладать всеми теми же свойствами, что и первое? Помимо доступности для наблюдения, более медленное движение встречало бы и меньшее сопротивление воздуха, которое (в случае его существенного вклада) обманчиво приводило к выводам в стиле Аристотеля.

В качестве такого вида движения Галилей выбрал скатывание гладкого шара по наклонной плоскости (см. рис.). Необходимо отметить, что последовательная теория такого плоскопараллельного движения не могла быть построена во времена Галилея. Однако знаний механической части курса общей физики достаточно, чтобы вывести выражение для ускорения шара:

где   — угол наклона плоскости к горизонту,  ,   — масса и радиус шара соответственно, а   — момент инерции шара относительно его центра. Для равномерно распределенного сплошного шара  . Выходит, что замечательным образом скатывание шара по наклонной плоскости оказывается равноускоренным! Интуитивно предполагая именно такой характер движения шара, Галилей поставил в т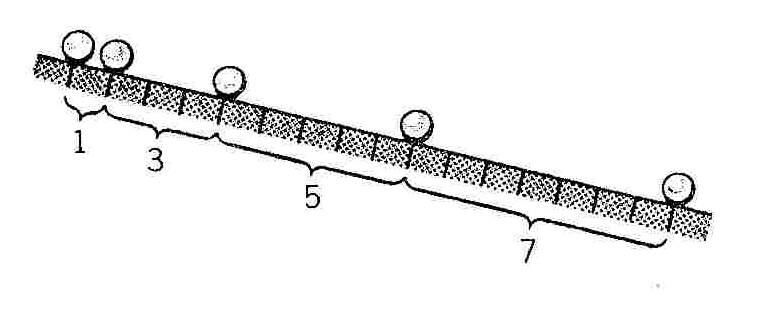 очках наклонной плоскости, которые шар должен пересечь в последовательные моменты времени (на расстояниях  ,  ,  ,   от ее вершины, в соответствии с законом равноускоренного движения  ) устройства, издававшие звук, когда шар прокатывался мимо (см. рис.). Далее, скатывая шар, он следил, действительно ли датчики звонят через равные промежутки времени. Поскольку точных часов в его время не было, для синхронизации Галилей использовал свой пульс или музыку играющего оркестра.

Г. Кавендиша.

Дата: 1797–1798

Методы: прецезионный эксперимент с использованием крутильных весов.

Прямота эксперимента: непосредственное измерение.

Искусственность изучаемых условий: лабораторные условия, чрезвычайно слабо выраженные эффекты.

Исследуемые фундаментальные принципы: закон всемирного тяготения.

 

    Итак, заявленная Ньютоном в законе всемирного тяготения пропорциональность силы гравитации обратному квадрату расстояния между телами была подтверждена сравнением центростремительного ускорения Луны и ускорения свободного падения на поверхности Земли. Также И. Ньютон показал, что из закона всемирного тяготения выводятся три закона Кеплера (см. раздел, посвященный закону всемирного тяготения). Осталось невыясненным только одно — чему же на самом деле равна константа  , определяющая силу гравитационного взаимодействия. Знание ее значения позволило бы «взвесить» Землю, т.е. вычислить ее массу, например, по ускорению свободного падения и известному радиусу Земли. Конечно же, можно было оценить массу Земли, предполагая, что она примерно однородна по плотности... Но это была бы грубая оценка, тем более что о внутренней структуре Земли во времена Кавендиша практически ничего не было известно (более того, со времен античности существовала теория полой Земли, которая была окончательно отвергнута только XX веке на основе сейсмических данных). С другой стороны, обнаружение гравитации в земных, лабораторных условиях полностью продемонстрировало бы несостоятельность теории вихрей Декарта.

 

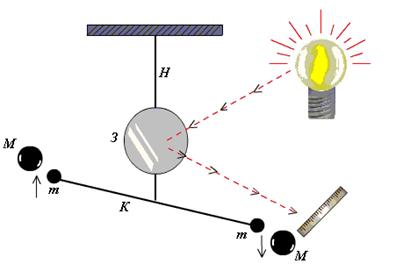
Эту чрезвычайно сложную задачу решил английский физик Генри Кавендиш (1731–1810), построив точнейший прибор для измерения силы — крутильные весы (см. рисунок справа выше). Они впервые были использованы Ш. Кулоном для измерения силы электростатического взаимодействия в 1784 г.; основные детали из конструкции были взяты Кавендишем практически без изменений и изображены на рисунке выше. Тонкая кварцевая нить Н привязывалась к середине коромысла К длиной 1,8м, на концах которого были уравновешены шарики массойm = 0,73кг. На нити также крепилось зеркальце З, так что поворот коромысла даже на малейший угол можно было проследить по сдвигу зайчика, отбрасываемого зеркальцем на шкалу. К шарикам, висящим на коромысле, одновременно подносили тяжелые шары массойM = 158кг, которые должны были их притягивать, приводя к повороту крутильных весов. Таким образом, момент силы гравитационного притяжения уравновешивался моментом упругой крутильной деформации кварцевой нити.

Несмотря на достаточно простую схему эксперимента, Г. Кавендишу пришлось предпринимать дополнительные шаги, чтобы получить хоть какие-то выходные данные. Для начала он вычислил коэффициент упругости нити, измерив период малых колебаний коромысла. Далее, чтобы минимизировать влияние тепловых потоков на отклонение весов от равновесия, Кавендиш поместил весь аппарат в деревянный ящик, в котором были только два маленьких отверстия, через которые под микроскопом он наблюдал за поворотом коромысла. Эксперимент Кавендиша являлся одним из первых прецезионных (т.е. высокоточных) измерений в истории физики. Действительно, наблюдавшаяся в нем сила притяжения была порядка  Н, что примерно эквивалентно тяжести одной сравнительно большой песчинки. Образно говоря, для того чтобы взвесить Землю, необходимо было взвесить песчинку.

Для сохранения исторической справедливости необходимо заметить, что измерение гравитационной постоянной не входило в планы Кавендиша — он задавался только задачей оценки массы (и, следовательно, средней плотности) Земли. Значение постоянной   даже не фигурирует в рукописях Кавендиша. Вместо этого он ограничивался рассуждением о том, что Земля во столько раз тяжелее массивного шара, во сколько вес маленького шарика больше силы его притяжения к массивному шару. Полученная Кавендишем масса Земли отличается не более чем на процент от современного значения 5.9736 × 10²⁴кг, значение же гравитационной постоянной составляет

Молекулярка і термодинаміка

 Р. Бойля, Е. Маріотта, Ж. Шарля, Ж. Гей-Люссака.

Современный взгляд термодинамики на идеальный неквантовый газ как термодинамическую систему описывается, пожалуй, двумя уравнениями, а именно термическим и калорическим уравнениями состояния:

Первое выражение задает давление газа как функцию его молярного объема   и температуры   и известно как уравнение Клапейрона–Менделеева; второе соотношение определяет молярную теплоемкость (т.е. теплоемкость моля) газа   в изохорном процессе. Символ   обозначает число степеней свободы частицы газа, включая три поступательных, а также (если таковые имеются) вращательные и колебательные степени свободы.

Роберт Бойль

Роберт Гук

Отто фон Герике

О днако если задаться вопросом об истории возникновения данных уравнений, окажется, что они являются результатом обобщения не одного, а нескольких экспериментальных фактов. Например, связь между давлением, объемом и температурой, выражаемая законом Клапейрона–Менделеева, исследовалась отдельно в системах с постоянным объемом, постоянным давлением и постоянной температурой. Более того, законы, связывающие две независимые термодинамические величины в этих случаях, носят имена различных ученых, открывших каждый из них.

Закон Бойля–Мариотта, как обычно считается, был открыт ирландским ученым Робертом Бойлем (1627–1691) в 1662 году и независимо от него французским исследователем Эдме Мариоттом (1620–1684) четырьмя годами позже. Этот закон утверждает, что давление идеального газа в изотермическом процессе обратно пропорционально объему,  . В эксперименте Бойля активно использовался вакуумный насос, изобретенный Отто фон Герике, известным также благодаря своим Магдебургским полушариям. По принципам, заложенным Герике, его для предполагаемых экспериментов перестроил ассистент Бойля Роберт Гук, который всесторонне исследовал зависимость между давлением и объемом газа. Бойль в своем трактате «Новые физико-механические эксперименты, относящиеся к упругости воздуха и связанным с ней эффектам» ссылался на то, что сформулирован закон именно Гуком — более того, чтобы остаться справедливым, он также упоминал работу Генри Пауэра (1623–1668) 1652 года, в которой этот закон был также описан.

 

В своем классическом эксперименте Бойль использовал J-образную трубку, запаянную с одного из концов. Если в такую трубку налить ртуть, то в запаянном конце останется некоторое количество воздуха, которое будет противостоять окончательному заполнению трубки ртутью (см. рис. выше, слева). Бойль заметил, что высота этого столбика уменьшается вдвое, если в результате доливания ртути ее уровень в правом колене трубки увеличили на высоту атмосферного столба. Действительно, если вначале ртути было достаточно мало, то в обоих коленах ее уровень был примерно одинаковым, так что в силу закона Паскаля в воздушном закутке слева было давление, близкое к атмосферному  . Предполагая высоту закутка малой, мы будем считать приблизительно неизменным и уровень ртути в нем. Если уровень ртути в правом колене поднимется на  , где   — плотность ртути, то давление в закутке обязано увеличиться на созданное этим столбом ртути гидростатическое давление, т.е. атмосферное давление  . В результате давление в закутке станет равным  , поэтому согласно закону Бойля–Мариотта его объем, а, стало быть, и высота, должны уменьшиться в два раза.

В другом опыте Бойля запаянная с одного конца трубка, нагретая на огне, открытым концом вводилась в вертикальную колбу с ртутью (см. рис. выше, справа). Когда трубка начинала охлаждаться, давление воздуха в ней падало, и часть ртути засасывалось внутрь. Теперь, опуская открытый конец трубки в колбу на разную глубину, можно было варьировать высоту избыточного столба ртути   — однако при этом менялся и воздушный столб  . В данном случае давление воздуха в воздушном закутке меньше атмосферного:

Бойль выяснил, что это давление обратно пропорционально высоте промежутка  .

И зучение зависимости между температурой, объемом и давленем интересовало французского инженера Жака Александра Сезара Шарля (1746–1823) в связи с разработкой воздушных шаров. Шарль изобрел горелку, которая поддерживала воздух внутри них в нагретом и расширенном состоянии — и в результате шар взлетал под действием силы Архимеда. Подъемная сила воздушного шара пропорциональна разности плотностей воздуха внутри него   и в окружающем пространстве  :

где   — объем шара. С другой стороны, воздушный шар Шарля не герметичен (в отличие от обычных воздушных шариков), поэтому давление внутри него равно атмосферному. Поэтому встает естественный вопрос: до какой температуры надо нагреть газ внутри шара, чтобы поднять в воздух груз заданной массы  ? Выражение для подъемной силы позволяет найти необходимую плотность внутри шара:

поэтому вопрос остается в неизвестной зависимости температуры   от плотности при заданном давлении  . Меняя температуру газа внутри шара, Шарль измерял подъемную силу и в итоге получил эту зависимость в виде обратной пропорциональности: Поскольку после

где мы записали плотность через массу газа и его объем. Таким образом, Шарлем была получена прямая пропорциональность между объемом и температурой при заданном давлении (1787). Сам Шарль также сравнивал изменение объема (т.е расширение) различных газов при их нагревании при постоянном давлении и заключил, что коэффициент теплового расширения

не зависит от природы газа и (фиксированного при нагреве) давления. Последнее выражение позволяет сделать универсальный газовый термометр, измеряющий абсолютную температуру напрямую. Действительно, при увеличении температуры на   объем любого идеального газа изменится на   процентов. 

Поскольку тепловое расширение газов активно изучалось различными учеными, закон Шарля был независимо от него открыт Жозефом Луи Гей–Люссаком (1778–1850) и Джоном Дальтоном (1766–1844). Более того, результаты Шарля 1787 года не были опубликованы, а стали известны благодаря тому, что Гей‑Люссак в своей работе 1802 года упомянул их, отдав приоритет открытия закона изобарного расширения Шарлю. Тем не менее, в русскоязычной литературе данный закон обычно называют законом Гей‑Люссака.

Жозеф Гей-Люссак

Джон Дальтон

Зависимость давления от температуры при постоянном объеме была получена Гильомом Амонтоном (1663–1705) — изобретателем усовершенствованного газового термометра (1695). Впоследствии эта зависимость исследовалась Гей‑Люссаком и Шарлем, поэтому закон, описывающий изохорный процесс, также в разных работах называется по-разному (в русскоязычной литературе — законом Шарля). Амонтон также изучал законы теплового расширения, поэтому внес вклад и в установление законов изобарного процесса. Во многом благодаря его вкладу в термометрию стали возможны точные исследования в рамках термодинамики как таковые.

Закон Шарля гласит, что при заданном объеме давление газа пропорционально температуре:

Этот закон имеет важное значение в рамках кинетической теории газа. Действительно, в этой теории давление газа создается его молекулами, ударяющимися о стенки сосуда и отдающими им часть своего импульса. Считая, что движение молекул беспорядочно и изотропно, можно получить основное уравнение молекулярно-кинетической теории, связывающее давление газа с плотностью и среднеквадратичой скоростью его молекул:

Иначе говоря, в правой части стоит плотность кинетической энергии, умноженная на две трети. В итоге из закона Шарля мы делаем вывод, что температура пропорциональна плотности кинетической энергии! Это объясняет, куда уходит энергия, затраченная на нагревание тела при постоянном объеме: в кинетическую энергию беспорядочного движения молекул! Таким образом, для идеального газа пробрасывается мостик между термическим и калорическим уравнениями состояни

+++

Опыт Штерна по измерению скоростей движения молекул в газе.

Дата: 1920.

Методы: количественные измерения в узком диапазоне параметров, в которых работает используемая теоретическая модель.

Прямота эксперимента: косвенный эксперимент.

Искусственность изучаемых условий: искусственные условия, специально подобранные, чтобы была применима используемая модель.

Исследуемые фундаментальные принципы: статистическое распределение частиц газа по скоростям.

Э кспериментальному подтверждению и визуализации распределения молекул газа по скоростям и был посвящен опыт Отто Штерна (1888–1969). Это еще один красивый опыт, позволявший в прямом смысле слова «начертить» график этого распределения на экспериментальной установке. Установка Штерна состояла из двух вращающихся полых цилиндров с совпадающими осями (см. рис. справа; большой цилиндр нарисован не полностью). Во внутреннем цилиндре, прямо по его оси была протянута серебряная нить 1, по которой пропускался ток, что приводило к ее нагреванию, частичному плавлению и последующему испарению атомов серебра с ее поверхности. В результате внутренний цилиндр, в котором изначально был вакуум, постепенно заполнялся газообразным серебром малой концентрации. Во внутреннем цилиндре, как показано на рисунке, была проделана тонкая щель 2, поэтому большая часть атомов серебра, долетая до цилиндра, оседала на нем. Малая же часть атомов проходила сквозь щель и попадала во внешний цилиндр, в котором поддерживался вакуум. Здесь эти атомы уже не сталкивались с другими атомами и поэтому двигались в радиальном направлении с постоянной скоростью, достигая внешнего цилиндра через время, обратное пропорциональное этой скорости:

где   — радиусы внутреннего и внешнего цилиндров, а   — радиальная компонента скорости частицы. В результате с течением времени на внешнем цилиндре 3 возникал слой серебряного напыления. В случае покоящихся цилиндров этот слой имел вид полоски, расположенной точно напротив щели во внутреннем цилиндре. Но если цилиндры вращались с одинаковой угловой скоростью  , то за время достижения молекулой внешнего цилиндра последний уже сдвигался на расстояние

по сравнению с точкой, стоящей прямо напротив щели (т.е. той точкой, на которую оседали частицы в случае неподвижных цилиндров). Как видим, частицы с различными значениями радиальной компоненты скорости порождают смещенные друг относительно друга полосы напыления на внешнем цилиндре. В результате на последнем действительно «рисуется» распределение атомов газообразного серебра по одной из проекций их скоростей, а именно по радиальной компоненте в точке пролета сквозь щель. Это распределение, как выяснилось, и совпадает с распределением Максвелла.

Опыт Перрена по определению масс молекул. Распределение Больцмана и теория броуновского движения Эйнштейна

Мариан Смолуховский

Альберт Эйнштейн

Жан Батист Перрен

Опыты Жана Батиста Перрена (1870–1942) окончательно замкнули серию исследований броуновского движения, начавшихся с самого Роберта Брауна. Как читатель мог узнать из раздела, посвященного истории этих исследований, к началу XX века взгляды на природу броуновского движения претерпели целую эволюцию. Тем не менее, математическая теория этого явления обязана появилась только в начале XX века благодаря работам польского математика Мариана Смолуховского (1872–1917) и физика-теоретика Альберта Эйнштейна (1879–1955)

Фактически, Перрен получил основные величины, характеризующие микроскопические масштабы молекулярно-кинетической теории: число Авогадро, постоянную Больцмана и характерные массы молекул. Кроме того, в опыте Перрена было подтверждено распределение Больцмана, а неявно — теория броуновского движения Эйнштейна и уравнение Фоккера–Планка, которые приводили к распределению Больцмана на основе механических (в терминологии Эйнштейна — субстатистических) соображений. Таким образом, благодаря данным теориям и описанному выше эксперименту науки о движении (механика) и о теплоте (термодинамика) были окончательно связаны на микроскопическом уровне.

Електрика

 Ш. Кулона,