Задание 4.
С вероятностью 0,954 определить ошибку выборки для среднего производственного стажа рабочих завода и для доли рабочих, имеющих стаж менее 5 лет. Указать пределы возможных значений этих показателей в генеральной совокупности. Какая должна быть численность выборки, чтобы ошибка этой выборки с этой вероятностью для производственного стажа не превысила 0,5 года?
Для расчета ошибки выборки используют теорема Чебышева - Ляпунова:
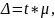
где
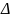- предельная ошибка,
μ – средняя ошибка,
t – коэффициент кратности ошибки.
Значения вероятностей ρ от t устанавливаются математической статистикой. По Таблице значений функции Лапласа, при ρ = 0,954 t = 2,0.
Распределение ряд распределения рабочих завода по общему стажу работы, с выделением пяти групп со следующими специализированными интервалами: 1) менее года; 2) от 1 до 2 лет; 3) от 3 до 5 лет; 4)от 6 до 10 лет; 5)от 11 лет и выше уже было представлено ранее.
Стаж работы – количественный признак, используется формула:
где N – объем генеральной совокупности,
n – объем выборки,
n/N и (1-n/N) – обследованная и необследованная часть совокупности соответственно,
– дисперсия
По
условию выборка 10%-ная, значит
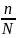= 0.1
n=100 чел
Дисперсия = 16,1 по предыдущим расчетам.
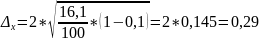
Определим ошибку выборки для доли рабочих, имеющих стаж менее 5 лет.
Признак альтернативный (либо стаж меньше 5 лет, либо нет).
Найдем предельную ошибку выборки:
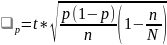
где t – коэффициент доверия (берется из таблицы Лапласа).
Вероятность равна 0,954, по таблице значений функций Лапласа t=2.
p – частота появления признака = среднее значение альтернативного признака
р
=
Следует найти пределы возможных значений этих показателей в генеральной совокупности.
-
+
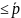
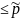0,71-0,043
0,71+0,043
0,580857 0,839143
Для вычисления необходимого объема выборки выразим его из формулы
причем
из условия
≤
0,5
значит, минимальный объем выборки для получения результата с заданной вероятностью – 95 наблюдений.
Задание 5.
Определить количественную взаимосвязь между признаками:
5.1. С помощью графического метода определить форму связи между производственным стажем и заработной платой рабочих цеха № 2 с № 1 по № 20 включительно (п=20).
5.2. Вычислить параметры уравнения регрессии, характеризующие зависимость между производственным стажем рабочих и их заработной платой. Построить на графике теоретическую и эмпирическую линии регрессии. Объяснить смысл полученных параметров уравнения.
5.3.Определить степень тесноты между рассматриваемыми признаками и существенность связи.
Суть графического метода заключается в построении поля корреляции – по сути точечного графика, где координаты каждой точки – значения факторного и результативного показателя (в данном варианте это стаж и зарплата соответственно).
Для определения параметров уравнений прямой на основе метода наименьших квадратов, основанного на свойствах средней арифметической решается система нормальных уравнений:
;
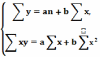Таблица 7 - Рабочие цеха №2 с №1 по №20
№ п/п |
производственный стаж, лет, х |
заработная плата,у.е. у |
х2 |
у2 |
х*у |
1 |
5 |
536 |
25 |
287296 |
2680 |
2 |
1 |
501 |
1 |
251001 |
501 |
3 |
3 |
517 |
9 |
267289 |
1551 |
4 |
15 |
571 |
225 |
326041 |
8565 |
5 |
1 |
492 |
1 |
242064 |
492 |
6 |
19 |
562 |
361 |
315844 |
10678 |
7 |
0 |
480 |
0 |
230400 |
0 |
8 |
5 |
541 |
25 |
292681 |
2705 |
9 |
7 |
535 |
49 |
286225 |
3745 |
10 |
1 |
502 |
1 |
252004 |
502 |
11 |
3 |
528 |
9 |
278784 |
1584 |
12 |
12 |
565 |
144 |
319225 |
6780 |
13 |
2 |
525 |
4 |
275625 |
1050 |
14 |
6 |
536 |
36 |
287296 |
3216 |
15 |
8 |
574 |
64 |
329476 |
4592 |
16 |
3 |
523 |
9 |
273529 |
1569 |
17 |
29 |
571 |
841 |
326041 |
16559 |
18 |
3 |
498 |
9 |
248004 |
1494 |
19 |
13 |
537 |
169 |
288369 |
6981 |
20 |
8 |
530 |
64 |
280900 |
4240 |
Итого: |
144 |
10624 |
2046 |
5658094 |
79484 |
Для выбранных n=20:
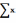=144,
=2046, 
=10624, 
=5658094, 
=79484.
Решим систему:
Итак, уравнение связи можно записать в виде: Y=509.86+2.96*x.
На рисунке 2 отмечена данная кривая, а также исходные данные (n=20) в виде точек и линии тренда к нему. Как можно увидеть, уравнение (прямая, теоретическая линия регрессии) буквально совпадает с линией тренда (эмпирической линией регрессии). Из этого можно сделать вывод, что формула подобрана, верно.
Рис. 2. Исходные данные, теоретическая и эмпирическая линии регрессии.
При наличии линейной зависимости степень тесноты связи определяется с помощью коэффициента парной корреляции или эмпирического корреляционного отношения. Определим коэффициент корреляции:
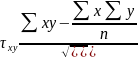
Положительный знак коэффициента снова говорит о наличии прямой связи, его величина достаточно близка к 1, так что связь тесна.
Оценка существенность коэффициента корреляции определяется на основании критерия его надежности:
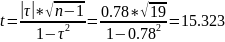
t >15,323>2.56, что говорит о существенности связи, то есть факториальный признак (стаж) оказывает существенное влияние на результативный (зарплата)