
Тематические обзоры по курсу элементарной математики
Составитель В.Г.Ермаков
Тема 3. Степень числа с рациональными показателями 1
3.1. Корень -ой степени
Определение.
Пусть
есть натуральное число и
 .
Корнем степени
из числа
.
Корнем степени
из числа
 называют такое число (если оно
существует),
-я
степень которого равна
.
называют такое число (если оно
существует),
-я
степень которого равна
.
Корень степени 2 называют также квадратным корнем. Корень степени 3 называют ещё кубическим корнем.
Пример 1.
Равенства
 показывают, что числа
показывают, что числа
 есть кубические корни
соответственно из чисел
есть кубические корни
соответственно из чисел
 .
.
Пример 2.
Равенства
 показывают, что числа
есть корни степени 5 соответственно
из чисел
показывают, что числа
есть корни степени 5 соответственно
из чисел
 .
.
Эти примеры указывают на то, что корни 3-й и 5-й степеней из действительных чисел существуют.
Пример 3.
Равенства
 показывают, что есть два числа
показывают, что есть два числа
 и
и
 ,
которые являются корнями четвертой
степени из
,
которые являются корнями четвертой
степени из
 ;
есть два числа
;
есть два числа
 и
и
 ,
являющиеся корнями четвертой
степени из 16; есть также два числа
,
являющиеся корнями четвертой
степени из 16; есть также два числа
 и
и
 ,
являющиеся корнями четвертой
степени из 81. Далее, 0 есть корень четвертой
степени из 0.
,
являющиеся корнями четвертой
степени из 81. Далее, 0 есть корень четвертой
степени из 0.
Этот пример указывает на то, что корень 4-й степени из неотрицательных чисел существует. Не существует корня четвертой степени из отрицательного числа, потому что четвертая степень любого действительного числа есть число неотрицательное.
Справедливы следующие теоремы.
Теорема 1. Существует, и притом, единственный, корень нечетной степени из любого действительного числа , при этом корень нечетной степени: а) из положительного числа есть число положительное; б) из отрицательного числа есть число отрицательное; в) из нуля есть нуль.
Теорема 2. Существуют два и только два корня четной степени из любого положительного числа, которые отличаются только знаками. Корень четной степени из 0 единственный, равный нулю. Корня четной степени из отрицательного числа не существует.
В школьном курсе математики
эти теоремы доказывают при помощи
графического метода, то есть путём
анализа графика функции
 соответственно при нечётных и чётных
значениях показателя
.
Строгое доказательство этих теорем
опирается на теорию непрерывных функций,
составляющую часть курса высшей
математики, изучаемого в высших учебных
заведениях.
соответственно при нечётных и чётных
значениях показателя
.
Строгое доказательство этих теорем
опирается на теорию непрерывных функций,
составляющую часть курса высшей
математики, изучаемого в высших учебных
заведениях.
3.2. Арифметический корень
Определение. Пусть
есть натуральное число и
.
Неотрицательный корень степени
из неотрицательного числа
 называют арифметическим корнем степени
из числа
.
называют арифметическим корнем степени
из числа
.
Как уже было отмечено в предыдущем
пункте, для нечетного
существует только один корень из любого
числа
.
При этом он неотрицательный, если
неотрицательно. Поэтому понятие корня
нечетной степени из неотрицательного
числа
и понятие арифметического корня той же
степени из того же самого числа
совпадают. В случае же четного
существуют два корня степени
из положительного числа. Один из них
является положительным, то есть является
арифметическим корнем степени
из числа
(его обозначают
 ),
а другой равен ему по
абсолютной величине, но противоположен
по знаку (он равен
),
а другой равен ему по
абсолютной величине, но противоположен
по знаку (он равен
 ).
Корень степени
).
Корень степени
 из нуля по определению есть
арифметический корень степени
из нуля:
из нуля по определению есть
арифметический корень степени
из нуля:
 .
.
Следует подчеркнуть, что:
1) если
– неотрицательное число,
а
– любое натуральное
число
 ,
то запись
означает арифметический корень
степени
из числа
.
,
то запись
означает арифметический корень
степени
из числа
.
2) если
– отрицательное число и
 – нечётное число, то запись
– нечётное число, то запись
 означает корень степени
означает корень степени
 из числа
,
но этот корень не является арифметическим
корнем;
из числа
,
но этот корень не является арифметическим
корнем;
3) если
– отрицательное число и
 – чётное число, то запись
– чётное число, то запись
 не имеет смысла.
не имеет смысла.
Теорема 3. Для натурального числа и неотрицательного числа справедливы равенства:
|
(1) |
|
(2) |
Доказательство. Так как – неотрицательное число, то по определению есть неотрицательное число, -я степень которого равна . Равенство (1) это и выражает.
Так как
 – неотрицательное число,
то, как следует из теорем 2д и 3д Дополнения
1,
– неотрицательное число,
то, как следует из теорем 2д и 3д Дополнения
1,
 .
При этом
.
При этом
 по определению есть неотрицательное
число, n-я
степень которого есть
по определению есть неотрицательное
число, n-я
степень которого есть
 .
Таким числом, очевидно, является число
,
что и выражает равенство (2). Заметим,
что другого неотрицательного
числа, n-я
степень которого равняется
,
нет.
.
Таким числом, очевидно, является число
,
что и выражает равенство (2). Заметим,
что другого неотрицательного
числа, n-я
степень которого равняется
,
нет.
Последнее утверждение докажем
методом от противного. В самом деле,
допустим, что существует положительное
число
 ,
такое, что
,
такое, что
 ,
но при этом
,
но при этом
 .
Тогда возможны 2 случая: либо
.
Тогда возможны 2 случая: либо
 ,
либо
,
либо
 .
В силу теоремы 3д Дополнения 1 в первом
случае
.
В силу теоремы 3д Дополнения 1 в первом
случае
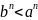 ,
а во втором случае
,
а во втором случае
 ,
что противоречит равенству
.
Из полученного противоречия вытекает,
что указанное число
является единственным.
,
что противоречит равенству
.
Из полученного противоречия вытекает,
что указанное число
является единственным.
Теорема 3 доказана.
Соображения, использованные при доказательстве теоремы 3, позволяют сформулировать и доказать ещё одну важную вспомогательную теорему.
Теорема 4.
Для любого натурального числа
и любых неотрицательных
действительных чисел
и
из равенства
 следует
следует
 .
.
Доказательство. Применим метод
доказательства от противного.
Предположим, что числа
и
неотрицательны,
,
но
 .
Тогда возможны 2 случая:
либо
.
Тогда возможны 2 случая:
либо
 ,
либо
,
либо
 .
В силу теоремы 3д Дополнения 1 и замечания
к этой теореме в первом случае
.
В силу теоремы 3д Дополнения 1 и замечания
к этой теореме в первом случае
 ,
а во втором случае
,
а во втором случае
 ,
что противоречит равенству
,
что противоречит равенству
 .
Из полученного противоречия вытекает,
что допущение о том, что
,
является ошибочным. Но тогда
.
Теорема 4 доказана.
.
Из полученного противоречия вытекает,
что допущение о том, что
,
является ошибочным. Но тогда
.
Теорема 4 доказана.
Теорема 4'.
Для любого нечётного натурального
числа

 и любых действительных чисел
и
из равенства
следует
.
и любых действительных чисел
и
из равенства
следует
.
Доказательство. В случае, когда оба
числа
и
неотрицательны, данное утверждение
является частью теоремы 4. Для случая,
когда оба эти числа отрицательны,
доказательство теоремы 4 можно повторить
почти дословно, но опорной теоремой
должна послужить не теорема 3д из
Дополнения 1, а близкая к ней теорема
5д. Наконец, в случае, когда числа
и
имеют разные знаки, легко заметить, что
их n-е степени
и
 тоже имеют разные знаки, следовательно,
и в этом случае доказательство можно
провести методом от противного.
тоже имеют разные знаки, следовательно,
и в этом случае доказательство можно
провести методом от противного.
Замечание. При доказательстве следующих теорем будут использованы свойства степени числа с целыми показателями, доказанные ранее.
Теорема (напоминание).
Пусть
и
– произвольные действительные числа,
отличные от нуля, а
и
 – произвольные целые числа. Тогда
– произвольные целые числа. Тогда
|
(1н) |
|
(2н) |
|
(3н) |
|
(4н) |
|
(5н) |
Теорема 5. Для
любого натурального числа
 и любых неотрицательных
действительных чисел
,
и
и любых неотрицательных
действительных чисел
,
и
 справедливы равенства
справедливы равенства
|
(3) |
|
(4) |
Доказательство. Возведём левую часть доказываемого равенства (3) в степень . По свойству (1), которое является прямым следствием определения корня -ой степени из неотрицательного действительного числа, имеем

Далее, возведём в степень правую часть доказываемого равенства (3). В силу свойств (1н) и (1) имеем

Правые части двух последних равенств равны, следовательно, равны и их левые части, то есть

Так как числа
 и
и
 неотрицательны, то, применяя теорему
4, получаем, что равенство (3) справедливо.
неотрицательны, то, применяя теорему
4, получаем, что равенство (3) справедливо.
Аналогично доказывается и равенство (4). Теорема 5 доказана.
Теорема 6. Для
любых натуральных чисел
и
 и любого неотрицательного
действительного числа
справедливы равенства
и любого неотрицательного
действительного числа
справедливы равенства
|
(5) |
|
(6) |
|
(7) |
Доказательство. По условию теоремы , поэтому числа, стоящие в левых и правых частях доказываемых равенств (5) – (7), определены и неотрицательны. Данное обстоятельство позволяет доказывать эти равенства с опорой на теорему 4.
Для доказательства равенства (5) возведём его левую и правую части в степень :


Из доказанного равенства
 в силу теоремы 4 вытекает справедливость
равенства (5).
в силу теоремы 4 вытекает справедливость
равенства (5).
Для доказательства равенства (6) возведём
его левую и правую части в степень
 :
:


Из доказанного равенства
 в силу теоремы 4 вытекает справедливость
равенства (6).
в силу теоремы 4 вытекает справедливость
равенства (6).
Для доказательства равенства (7) возведём его левую и правую части в степень :


Из доказанного равенства
 в силу теоремы 4 вытекает справедливость
равенства (7).
в силу теоремы 4 вытекает справедливость
равенства (7).
Теорема 6 доказана.
Замечание. Если и – нечётные числа, то равенства (5) – (7) справедливы для любых действительных чисел , необязательно неотрицательных. Доказательство этого утверждения можно получить дословным повторением доказательства теоремы 6, но главной опорой при этом должна быть не теорема 4, а теорема 4'.
Теорема 7. Для любого натурального числа и любого действительного числа справедливо равенство
|
(8) |
Доказательство. Пусть есть произвольное действительное число. Тогда

Поэтому в силу равенства (2)

что и требовалось доказать.
Теорема 7 доказана.
Теорема 8.
Пусть
– положительное число,
 – целое число и
– натуральное число,
.
Тогда справедливо равенство
– целое число и
– натуральное число,
.
Тогда справедливо равенство
|
(9) |
Доказательство. Если – натуральное число, то в этом случае равенство (9) совпадает со свойством (5) и потому уже доказано.
Если
 ,
то
,
то

Следовательно,
 .
.
Если
 ,
то
,
то
 ,
где
,
где
 – натуральное число. Тогда, используя
определение степени с отрицательным
целым показателем и свойства арифметических
корней степени
,
получаем:
– натуральное число. Тогда, используя
определение степени с отрицательным
целым показателем и свойства арифметических
корней степени
,
получаем:

Теорема 8 доказана.

 ,
,
 ;
; ;
; ;
; ;
;
 ;
;
 ;
; ;
; .
.
