1.3. Взвешенные скользящие средние (wma).
При всей простоте вычисления и ясности интерпретации простой скользящей средней ей присущи определенные недостатки, важнейшими из которых являются следующие:
- простая МА относится к индикаторам, подающим по два разных сигнала на одних и тех же данных, в первый раз, когда новые данные включаются в расчет, и вторично, когда те же данные выпускаются из скользящего окна данных, подвергающихся обработке. Очевидно, что реальный рынок не может реагировать на предпринятое аналитиком перемещение скользящего окна вперед. Поэтому любой индикатор, находящийся в сильной зависимости от прошлых данных, вносит в исследование элемент случайных ошибок; - простая МА будет подавлять циклические компоненты графика цен с периодами, равными интервалу усреднения и укладывающимися в него целое число раз.
И тот и другой недостаток относятся к так называемым краевым эффектам в обработке временных рядов, когда для вычислений используется некоторый ограниченный участок ряда. Для того, чтобы исключить краевые эффекты используются так называемые взвешенные временные окна, что применительно к вычислению скользящих средних сводится к следующей модификации алгоритма суммирования:
WMA = (Сумма Сi*Wi)/ (Сумма Wi),
где Wi - некоторые весовые значения, придаваемые ценам при суммировании.
Есть различные подходы к заданию весовых значений, однако наиболее распространенным в техническом анализе является метод, при котором более поздним значения придается наибольший вес.
1.3.1. Экспоненциальная ма (ема).
Формула расчета экспоненциально-сглаженной МА - ЕМА имеет следующий вид:
EMA(n) = EMA(n - 1) + K x [Price(n) - EMA(n - 1)],
где n - текущий момент времени, n - 1 - предыдущий момент времени, K = 2 / (m + 1), m - период средней.
Главное достоинство ЕМА в том, что она включает в себя все цены предыдущего периода, а не только отрезок, заданный при установке периода. При этом более поздним значениям придается больший вес. .
1.3.2. Линейно-сглаженные ма.
В случае линейно-сглаженной МА весовые коэффициенты при суммировании выбираются следующим образом:
LMA(m) = C(n)(m)+C(n-1)*(m-1)+:+ C(n-m+1)*1/(1+2+3+:+m),
т.е. текущему значению цены соответствует наибольший вес m, а самому удаленному, принимающему участие в вычислении МА - вес 1.
На представленном рисунке приведены примеры различных типов скользящих средних с одинаковым периодом, вычисленных по одним и тем же ценовым значениям.
Рис.4. Пример скользящих средних различного типа с периодом 21, нанесенных на одном графике цен:
SMA - простая скользящая средняя; EMA - экспоненциально-сглаженная скользящая средняя; TMA - треугольно-сглаженная скользящая средняя; WMA - взвешенная скользящая средняя.
Из представленных данных видно, что характер поведения всех скользящих средних приблизительно одинаков. На практике чаще всего применяют экспоненциальную скользящую среднюю.
1.4. Смещенные вперед скользящие средние.
Скользящая средняя сдвигается по графику вперед. Сигнал - пересечение средней со смещенной средней. Применение смещенных скользящих средних эквивалентно применению осциллятора Моментум, который мы рассмотрим позднее, к скользящей средней.
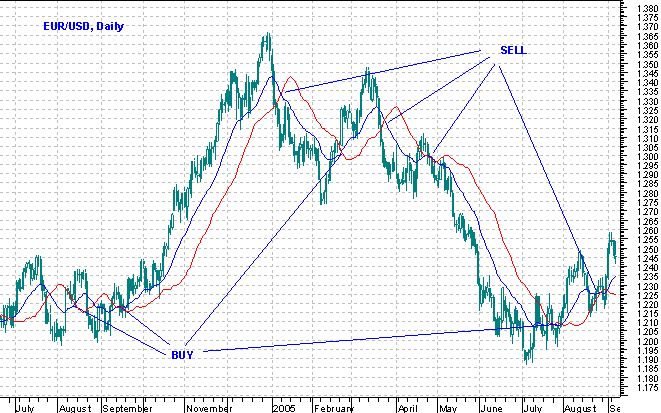
Рис. 5. Применение смещенных вперед скользящих средних. Синим цветом показана ЕМА с периодом 21, красным - та же ЕМА, смещенная на 10 интервалов графика вперед.
Из представленного рисунка видно, что на трендовом рынке смещенная МА также дает хорошие торговые сигналы, однако в боковом тренде подаваемые сигналы будут ложными и приведут к убыткам.
Смещенные скользящие средние нашли широкое применение среди трейдеров. В частности на комбинации трех различных смещенных средних с разными периодами и отличающимся смещением построен популярный среди некоторых трейдеров индикатор Аллигатор, предложенный Б.Вильямсом.
Комбинации нескольких скользящих средних на одном графике широко используются также в мультифреймовом анализе, когда движение цены рассматривается одновременно по нескольким тайм-фреймам. Детали этого подхода находятся за рамками нашего изложения и достаточно широко описаны в литературе.