8 білетів в дві чотиримісні театральні ложі випадковим чином розподілені серед групи, що складається з 4 чоловіків та 4 жінок. Знайти ймовірність того, що в кожній ложі чоловіків і жінок опиниться порівну.
Дана схема включення елементів.
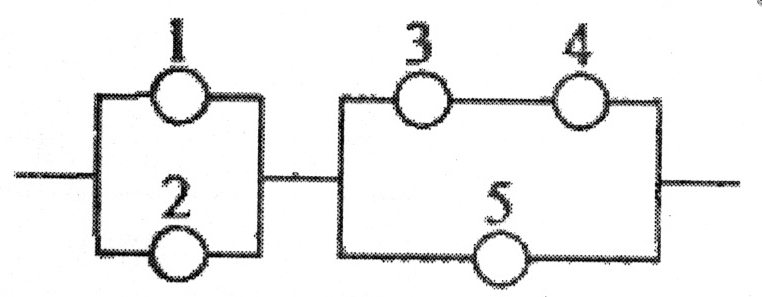
Умови задачі див. у додатку 1(зразок 1, п. 2).
Медичний аналіз виявляє у хворого хворобу α з ймовірністю р1 і помилково вказує на цю хворобу при її відсутності з ймовірність р2. У хворих направлених на аналіз з попереднім діагнозом хвороби α ця хвороба зустрічається з ймовірністю р.
3.1. Знайти ймовірність Р(А) того, що у пацієнта аналіз вкаже на хворобу.
3.2. Вирахувати Р(А) при р=0,6, р1=0,8, р2=0,05.
3.3. Вирахувати по формулі Байеса ймовірність того, що у пацієнта дійсно є хвороба α, якщо на неї вказали аналізи.
За період в131 рік з 1865 по 1995 рр. в Санкт-Петербурзі 10-го січня середня температура нижче -100 (подія А) спостерігалась 44 рази, а нижче – 300 (подія В) – всього 1 раз (-33,60 в 1987 р.). Виходячи з цих статистичних даних приймемо Р(А)=44/131=0,34, Р(В)=1/131=0,008.
4.1. Знайти ймовірність події, яка означає, що найближчі 4 роки подія А буде спостерігатися не менше 2 разів.
4.2. За допомогою наближеної формули Пуассона знайти ймовірність появи події В хоч би в одному році з наступних 50 років.
Два знаряддя залпом стріляють по цілі до першого попадання хоча б одним знаряддям. Ймовірність попадання кожного =0,6.
5.1. Знайти закон розподілення випадкової величини Х, рівної числу залпів.
5.2. Вирахувати мх.
5.3. Знайти Р (Х< мх).
Надано:
Умови задачі див. у додатку 1(зразок 1, п. 6).
Зроблено 2 незалежних виміри приладом без систематичної помилки (мх=0). Середня квадратична помилка бх =2м. Знайти ймовірність Р того, що помилка хоча б одного виміру по модулю буде менша бх. Припускаємо, що помилка вимірювання Х розподілена нормально.
Надано: р11=0,25 р12=0,1, р21=0,15, р22=0,5.
Умови задачі див. у додатку 1(зразок 1, п. 8).
Надано: D – криволінійний трикутник обмежений лініями:
,
де х =0; у=0. Умови задачі див у додатку 1(зразок 1, п.9).