Розв’язок трансцендентних рівнянь.

При рішенні трансцендентних рівнянь для отримання розв’язок в явному вигляді перед командою solve слід ввести додаткову команду _EnvExplicit:=true. Приклад розв’язок складної системи трансцендентних рівнянь і спрощення виду рішень:

> eq:={ 7*3^x-3*2^(z+y-x+2)=15, 2*3^(x+1)+

3*2^(z+y-x)=66, ln(x+y+z)-3*ln(x)-ln(y*z)=-ln(4) }:

> _EnvExplicit:=true:

> s:=solve(eq,{x,y,z}):

> simplify(s[1]);simplify(s[2]);

{x=2, y=3, z=1} {x=2, y=1, z=3}

Розв’язок нерівностей Розв’язок простих нерівностей.

Команда solve застосовується також для розв’язків нерівностей. Розв’язок нерівності видається у вигляді інтервалу зміни шуканої змінної. В тому випадку, якщо розв’язок нерівності напіввісь, то в полі висновку з'являється конструкція вигляду RealRange(–, Open(a)), яка означає, що x(–, а), а – деяке число. Слово Open означає, що інтервал з відкритою межею. Якщо цього слова немає, то відповідна межа інтервалу включена в безліч рішень. Наприклад:

> s:=solve(sqrt(x+3)<sqrt(x-1)+sqrt(x-2),x):

> convert(s,radical);

RealRange

Якщо ви хочете отримати розв’язок нерівності не у вигляді інтервальної безлічі типу x(а, b), а у вигляді обмежень для шуканої змінної типу a<x, x< b, то змінну, щодо якої слід дозволити нерівність, слід указувати у фігурних дужках. Наприклад:

> solve(1-1/2*ln(x)>2,{x});

Розв’язок систем нерівностей.

За допомогою команди solve можна також вирішити систему нерівностей. Наприклад:

> solve ({x+y>=2,x-2*y<=1,x-y>=0,x-2*y>=1},{x,y});

Завдання.

Дано число а=57/13. Знайти його цілу частину x і дробову частину у та переконатися, що a=x+y.
Дано комплексне число . Знайти його дійсну та уявну частини, а потім комплексно зв'язане йому число w і переконатися, що w+z=2Re(z).
Знайти модуль і аргумент комплексного числа і обчислити z⁴.
^{Знайти
всі розв’язки системи рівнянь} ^{та суму двох наборів рішень.}
Чисельно розв’яжіть рівняння .
Знайдіть функцію f(x), що задовольняє рівнянню
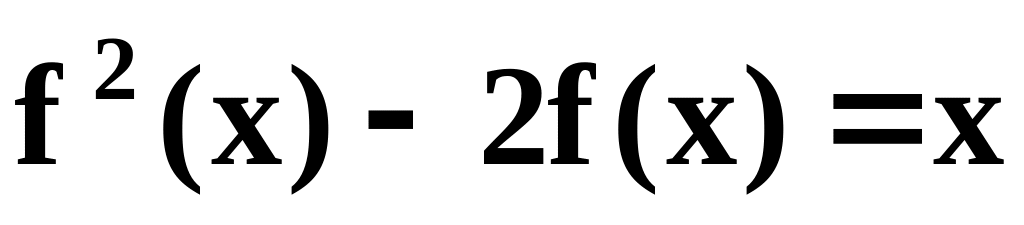
Знайдіть всі розв’язки рівняння .
Розв’яжіть нерівність . Запишіть цей результат в аналітичному вигляді. Отримайте рішення цієї нерівності у вигляді обмежень для шуканої змінної.
Розв’яжіть нерівність .
Дано комплексне число . Знайти його дійсну і уявні частини, алгебраїчну форму, модуль і аргумент.
Записати функцію у вигляді функціонального оператора і обчислити її значення при x=1, y=0 і при , .
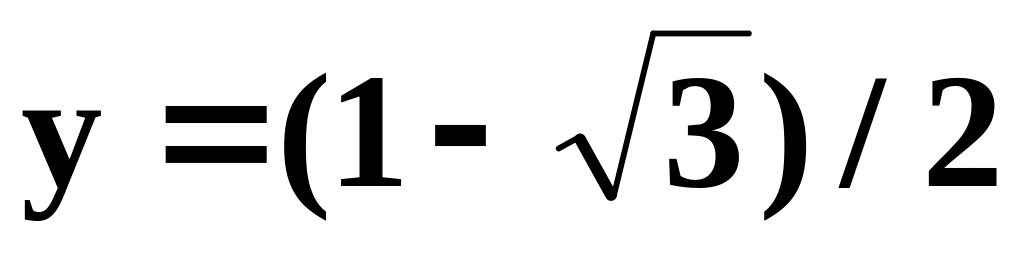Записати функцію 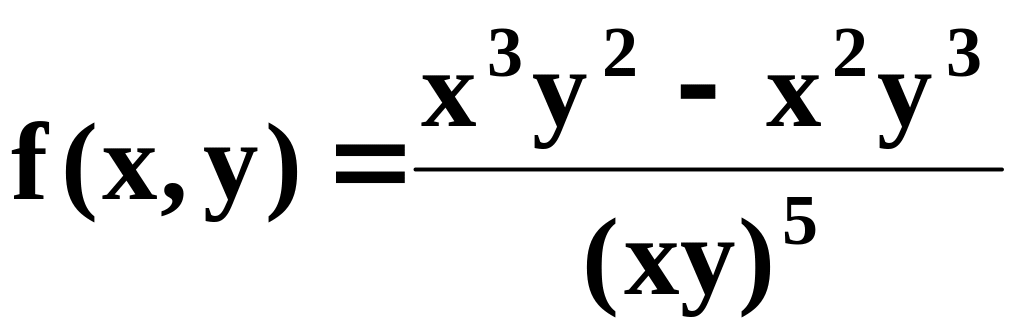за допомогою оператора привласнення і обчислити її значення при x=a, y=1/a, використовуючи команду підстановки subs.
Знайти всі точні рішення системи в аналітичному вигляді.
Знайти всі розв’язки тригонометричного рівняння .
Знайти чисельне розв’язки рівняння .
Вирішити нерівність .