Інтегрування

Невизначений інтеграл обчислюється за допомогою 2-х команд: прямого виконання - int(f, x), де f - подынтегральная функція, x - змінна інтеграції; відкладеного виконання - Int(f, x) - де параметри команди такі ж, як і в команді прямого виконання int. Команда Int видає на екран інтеграл в аналітичному виді математичної формули. Для обчислення певного інтеграла в командах int і Int додаються межі інтеграції, наприклад

> Int((1+cos(x))^2, x=0..Pi)=int((1+cos(x))^2, x=0..Pi);

Якщо в команді інтеграції додати опцію continuous: int(f, x, continuous), то Maple ігноруватиме будь-які можливі розриви підінтегральної функції в діапазоні інтеграції. Це дозволяє обчислювати невласні інтеграли від необмежених функцій. Невласні інтеграли з нескінченними межами інтеграції обчислюються, якщо в параметрах команди int указувати, наприклад, x=0..+infinity.

Чисельна інтеграція виконується командою evalf(int(f, x=x1..x2), e), де e - точність обчислень (число знаків після коми).

Інтеграли, залежні від параметра. Обмеження для параметрів.

Якщо вимагається обчислити інтеграл, залежний від параметра, то його значення може залежати від знака цього параметра або яких-небудь інших обмежень. Розглянемо як приклад інтеграл, який, як відомо з математичного аналізу, сходиться при а>0

і розходиться при а<0. Якщо обчислити його відразу, то вийде:

> Int(exp(-a*x),x=0..+infinity)=int(exp(-a*x),x=0..+infinity);

Definite integration: Can't determine if integral is convergent.

Need to know sign --> а

Will now try indefinite integration and then take limits.

.

У такий спосіб інтеграл з параметром не обчислити. Для отримання явного аналітичного результату обчислень слід зробити які-небудь припущення про значення параметрів, тобто накласти на них обмеження. Це можна зробити за допомогою команди assume(expr1), де expr1 - нерівність. Додаткові обмеження вводяться за допомогою команди additionally(expr2), де expr2 - інша нерівність, обмежуюче значення параметра з другого боку.

Після накладення обмежень на параметр Maple додає до його імені символ (~), наприклад параметр а, на який були накладені деякі обмеження, в терміні висновку матиме вигляд: a~.

Опис накладених обмежень параметра а можна викликати командою about(a). Приклад: накласти обмеження на параметр а такі, що a>-1, а≤3:

> assume(a>-1); additionally(a<=3);

> about(a);

Originally а, renamed a~:

is assumed to be: RealRange(Open(-1),3)

Дії з матрицями

Визначення матриці.

Для визначення матриці в Maple можна використовувати команду matrix(n, m [[a11,a12…,a1n], [a21,a22…,a2m]… [an1,an2…,anm]]), де n  число рядків, m – число стовпців в матриці. Ці числа задавати необов'язково, а достатньо перерахувати елементи матриці порядково в квадратних дужках через кому. Наприклад:

> А:=matrix([[1,2,3],[-3, -2, -1]]);

В Maple матриці спеціального вигляду можна генерувати за допомогою додаткових команд. Зокрема діагональну матрицю можна отримати командою diag. Наприклад:

> J:=diag(1,2,3);

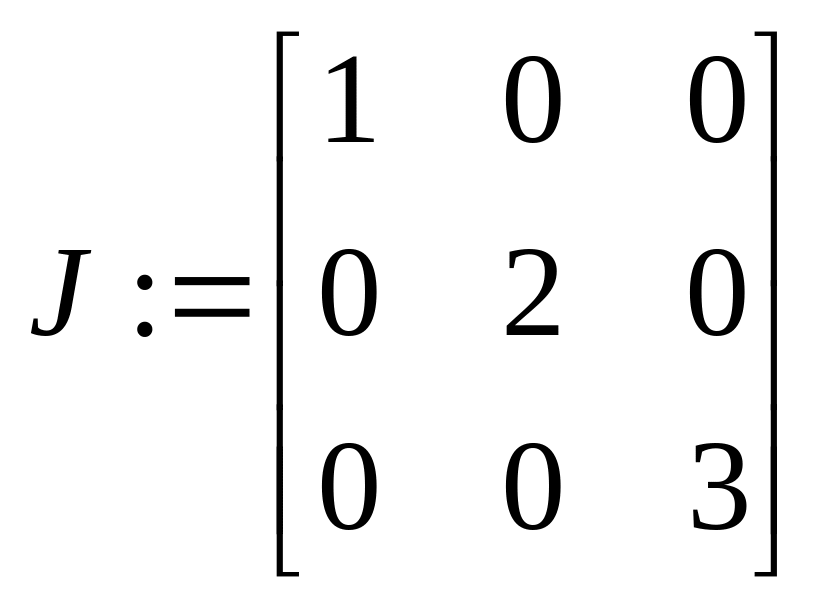
Генерувати матрицю можна за допомогою функції f(i, j) від змінних i, j – індексів матриці: matrix(n, m, f), де де n - число рядків, m – число стовпців. Наприклад:

> f:=(i, j)->x^i*y^j;

> А:=matrix(2,3,f);

Число рядків в матриці А можна визначити за допомогою команди rowdim(A), а число стовпців – за допомогою команди coldim(A).

Арифметичні операції з матрицями.

Складання двох матриць однакової розмірності здійснюється командами:

evalm(A+B) або matadd(A,B). Добуток двох матриць може бути знайдений за допомогою двох команд:

1. evalm(A&*B);

2. multiply(A,B).

Як другий аргумент в командах, що обчислюють добуток, можна вказувати вектор, наприклад:

> А:=matrix([[1,0],[0, -1]]);

> B:=matrix([[-5,1] [7,4]]);

> v:=vector([2,4]);

> multiply(A,v);

> multiply(A,B);

> matadd(A,B);

Команда evalm дозволяє також додавати до матриці число і множити матрицю на число. Наприклад:

> С:=matrix([[1,1],[2,3]]):

> evalm(2+3*С);

Визначники, мінори і алгебраїчні доповнення. Ранг і слід матриці.

Визначник матриці А обчислюється командою det(A). Команда minor(A,i,j) повертає матрицю, отриману з початкової матриці А викреслюванням i-ого рядка і j-ого стовпця. Мінор Mij елемента aij матриці А можна обчислити командою det(minor(A,i,j)). Ранг матриці А обчислюється командою rank(A). Слід матриці А, рівний сумі її діагональних елементів, обчислюється командою trace(A). 7

> А:=matrix([[4,0,5],[0,1, -6],[3,0,4]]);

> det(A);

1

> minor(А,3,2);

> det(%);

-24

> trace(A);

9

Зворотня і транспонована матриці.

Зворотну матрицю А^1, таку що А^1А=АА^1=Е, де Е  одинична матриця, можна обчислити двома способами:

1. evalm(1/A);

2. inverse(A).

Транспонування матриці А – ця зміна місцями рядків і стовпців. Отримана в результаті цього матриця називається транспонованою і позначається А'. Транспоновану матрицю А' можна обчислити командою transpose(A).

Наприклад, використовуючи задану в попередньому пункті матрицю А, знайдемо зворотню до неї і транспоновану:

> inverse(A);

> multiply(A,%);

> transpose(A);

З'ясування типу матриці.

З'ясувати позитивну або негативну визначеність матриці можна за допомогою команди definite(A,param), де param може приймати значення: 'positive_def' – позитивно визначена (A>0), 'positive_semidef' –ненегативно визначена , 'negative_def' – негативно визначена (A<0), 'negative_semidef'  непозитивно визначена . Результатом дії буде константа true – підтвердження, false – заперечення зробленого припущення. Наприклад:

> А:=matrix([[2,1],[1,3]]);

> definite(А,'positive_def');

true

Перевірити ортогональність матриці А можна командою orthog(A).

> В:=matrix([[1/2,1*sqrt(3)/2]

[1*sqrt(3)/2, -1/2]]);

> orthog(В);

true

Функції від матриць.

Зведення матриці А в ступінь n проводиться командою evalm(A^n). Обчислення матричної експоненти можливо за допомогою команди exponential(A). Наприклад:

> Т:=matrix([[5*a,2*b],[-2*b,5*a]]);

> exponential(Т);

> evalm(Т^2);