1.3. Параллактический треугольник светила и его решение.

• Понятие параллактического треугольника

• Решение параллактического треугольника

Понятие параллактического треугольника.

Построив для данной широты небесную сферу и проведя вертикал и меридиан светила С, получим сферический треугольник, ZР_NC, вершинами которого являются повышенный полюс мира P_N, зенит наблюдателя Z и место светила С. Этот треугольник называется параллактическим треугольником светила. Элементами параллактического треугольника являются: угол при зените - азимут полукругового счета А; угол при полюсе - местный часовой практический угол t, отсчитываемый от меридиана данного наблюдателя; угол при светиле, который называется параллактическим углом (q) и в практике мореходной астрономии применяется редко; сторона ZP_N - дополнение широты до 90°, т. е. 90° - ; сторона Р_NС - дополнение склонения до 90°, или полярное расстояние = 90° - ; сторона ZC - дополнение высоты до 90°, или зенитное расстояние z = 90° - h.

Решение параллактического треугольника.

Основным содержанием практической мореходной астрономии является переход от одной системы координат к другой. В большинстве задач приходиться переходить от 1-ой экваториальной системы координат к горизонтной. Для этого решается параллактический треугольник.

Применим формулу косинуса стороны к стороне ZC. В сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих же сторон и на косинус угла между ними.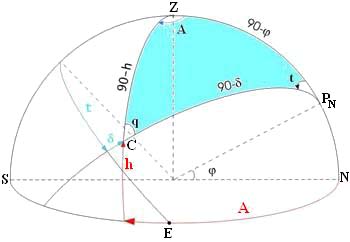

cos(90 - h) = cos(90 - ) cos(90 - ) + sin(90 - ) sin(90 - )cost_м

Применив формулы приведения, окончательно получим:

sinh = sin sin + cos cos cost_м       (1.1)

Применим формулу котангенсов к 4-м рядом лежащим элементам:

А, (90 - ), t_м и (90 - )

В сферическом треугольнике произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны и минус произведение косинусов средних элементов.

ctgAsint_м = ctg(90 - ) sin(90 - ) - cos(90 - )cost_м

Или окончательно после преобразования получим:

ctgA = tg cos cosect_м - sin ctgt_м       (1.2)

Как видно из этих формул, параллактический треугольник связывает небесные координаты - горизонтные h и А и экваториальные и t - с географическими координатами наблюдателя (широта прямо входит в параллактический треугольник, а долгота входит косвенно согласно формулы t_м = t_гр ± . Данные формулы применяются при определении места судна (при расчете элементов высотной линии положения) и для определении поправки компаса.

1.4. Дифференциальные формулы мореходной астрономии.

• Дифференциальные формулы мореходной астрономии.

• Изменение координат светил вследствие видимого суточного движения.

Дифференциальные формулы мореходной астрономии.

Как было показано в предыдущем параграфе высота и азимут являются функциями трех независимых переменных:

, и t: h = f( , ,t) A = F( , ,t)

Найдём частные производные (вывод пропускаем):

Переходя к конечным приращениям, получим следующие формулы:

h = cosA	(1.3)	A = tghsinA	(1.6)
h = cosq	(1.4)	A = -sinqsech	(1.7)
ht = -cos sinA t	(1.5)	A t = -cosqcosqsech t	(1.8)

Данные формулы лежат в основе таблиц ВАС-58, объясняют характер изменения горизонтных координат светил вследствие суточного движения и наивыгоднейшие условия определения поправки компаса.

Изменение координат светил вследствие видимого суточного движения.

Рассмотрим формулу (1.5), которая позволяет объяснить закономерности изменения высоты вследствие видимого суточного движения.

1. Когда светило находится на первом вертикале (А = 90° или 270°), то sinA достигает максимального значения, следовательно, изменение высоты светила максимальное.

2. Когда светило находится на меридиане наблюдателя (А = 0° или 180°), то sinA=0, следовательно, высота светила практически не изменяется.

3. Если наблюдатель находится на полюсе ( = 90°), то cos =0, следовательно, высоты всех светил в суточном вращении не изменяются. Такой же вывод, но графический дается в следующем параграфе.

Рассмотрим формулу (1.8). В момент верхней кульминации, как будет показано далее, высота светила достигает максимального значения. Т.к. светило находится на меридиане наблюдателя, то параллактический угол q = 0° или q = 180°. Следовательно, cosq и sech достигают максимального значения, и азимут в момент верхней кульминации изменяется максимально быстро.