Линейные дифференциальные уравнения n‑го порядка. Вронскиан. Фундаментальная система решений.

Линейное уравнение n-го порядка имеет следующий общий вид: y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ' + pn (x) y = f (x). (10.1)

Если в рассматриваемом интервале изменения x функция f (x) тождественно равна нулю, то уравнение (10.1) принимает вид: y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ' + pn (x) y = 0. (10.2)

и называется однородным. Если f (x) ≠ 0, то уравнение (10.1) называется неоднородным. Ниже показано, что, как и в случае линейного уравнения первого порядка, интегрирование неоднородного линейного уравнения (10.1) приводится к интегрированию однородного уравнения.

Основное предположение

Будем предполагать, что функции p1, …, pn, f (x) непрерывны в интервале (a, b). Это предположение обеспечит существование и единственность решения задачи Коши с любыми y0, У`o, …,Yo<sup>(n-1)</sup> при любом x ∈ (a, b). В частности, единственным решением однородного уравнения (10.2) с нулевыми начальными условиями y0 (x0) = 0, У`o (x0) = 0, …, Yo^(n-1) (x0) = 0 — будет только очевидное нулевое решение y = 0.

Дадим признак линейной независимости n частных решений (11.3) однородного линейного уравнения n-го порядка. С этой целью введем в рассмотрение определитель, составленный из данных частных решений и их производных до порядка n – 1 включительно:

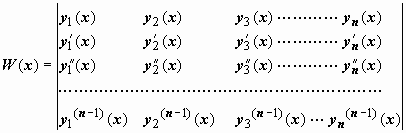
Этот определитель называется определителем Вронского решений y1, y2, …, yn.

Уравнение, допускающее интегрирующий множитель.

Уравнение в полных дифференциалах

dU = 0

U = C

U (x ,y) = C

Может быть , что левая часть уравнения :

M (x ,y) dx + N(x , y ) dy = 0 (2.8)

является полным дифференциалом некоторой функции U (x, y)

dU (x, y) = M (x, y) dx + N (x , y) dy =>уравнение (2.8) принимает вид dU (x , y) = 0

Если функция y(x) является решением уравнения (2.8) тогда dU (x, y(x)) 0 сл-но

U (x, y(x))= c (2.9)

C= const

И наоборот, если некоторая функция y(x) обращается в тождество конечное уравнение (2.9) , то дифференцируя это тождество получим:

dU (x, y (x)) = 0, значит U (x, y) = C является общим интегралом исходного уравнения.

Для того чтобы левая часть уравнения (2.8) является полным дифференциалом некоторой функции U (x , y) необходимо и достаточно условие Эйлера

(2.10)

dU(х,у)=

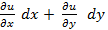
Если условие Эйлера выполняется, то уравнение (2.8) легко интегрировать

dU = Mdx + Ndy

dU=

При вычиcлении интеграла величина у рассматривается как const , поэтому c(y) является произвольной функцией y. Для определения функции C(y) дифференцируем найденную функцию U(x, y) по y и так как , получим : (

В некоторых случаях, когда левая часть уравнения (2.8) не является полным дифференциалом, легко удается подобрать функцию после умножения на которую левая часть уравнения (2,8) превращается в полный дифференциал, то есть dU = µ Mdx + µ Ndy и в этом уравнение эти функции удовлетворяют условию Эйлера.

Такая функция µ называется интегрируемым множеством. Заметим, что умножение может привести к появлению посторонних решений , обращающих µ(x, y) в 0

В общем случае не всегда так легко удаётся найти интегрир. множитель.

Вообще, надо подобрать хотя бы одно ненулевое решение уравнения:

(2.11)

Вообще задача интегрирования (2.11) ничуть не проще задачи интегрирования (2.10)

Однако, если мы можем считать µ функцией только одной переменной будь то x, y, х²+у² и т.д., то задача существенно упрощается .

Например, найдём условие, когда µ можно найти как функцию от х

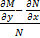; считаем это выражение непрерывной функцией х.

Проинтегрируем и получим

Ln µ =

M= C * (2.12)

Можно считать c=1, так как нам нужен хотя бы один интегрирующий множитель

Если является функцией только x, то интегрирующий множитель найдется по формуле(2.12)

Аналогично можно выписать условие при которых интегрирующий множитель зависит от другой выбранной переменной .