
- •Виды дифференциальных уравнений. Интеграл дифференциального уравнения. Общий интеграл. Интегральная кривая.
- •Задача Коши. Существование и единственность решений уравнений n-го порядка и систем уравнений.
- •Уравнения вида , .
- •Уравнение в полных дифференциалах.
- •Линейные обыкновенные дифференциальные уравнения первого порядка. Метод Лагранжа.
- •Линейные дифференциальные уравнения n‑го порядка. Вронскиан. Фундаментальная система решений.
- •Уравнение, допускающее интегрирующий множитель.
- •Однородное дифференциальное уравнение первого порядка.
- •Уравнение Риккати
- •Уравнение Лагранжа.
- •Уравнение Клеро.
- •Уравнение Бернулли.
- •Задача Коши для дифференциальных уравнений в частных производных первого порядка.
- •Сведение систем дифференциальных уравнений к одному уравнению более высокого порядка.
- •Однородные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение.
- •1 Случай :
- •2 Случай :
- •3 Случай:
- •Запись системы в симметрической форме. Нахождение интегрируемых комбинаций.
- •Линейные неоднородные уравнения. Отыскание частного решения в случае уравнения с квазиполиномом.
- •Типы точек покоя. Фокус, центр.
- •Линейные неоднородные уравнения. Отыскание частного решения методом вариации произвольных постоянных.
- •Системы дифференциальных уравнений. Запись задачи в матричной форме.
- •Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
- •Случай :
- •Случай :
- •Интегрирование линейных уравнений при помощи степенных рядов
- •Устойчивость решений дифференциальных уравнений. Асимптотическая устойчивость.
- •Типы точек покоя. Узел, седло.
- •Линейные и Квазилинейные уравнения частных производных
- •Уравнения с разделяющимися переменными.
- •Система дифференциальных уравнений с частными производными 1-го порядка
- •Простейшие оду первого порядка, разрешенные относительно производной.
Виды дифференциальных уравнений. Интеграл дифференциального уравнения. Общий интеграл. Интегральная кривая.
Виды д\у:
-
Уравнения
с разделяющимися переменными:
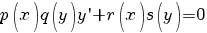
-
Однородные
уравнения:
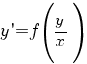
-
Линейные
дифференциальные уравнения:
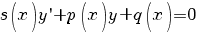
-
Уравнения
Бернулли:
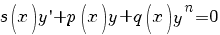
-
Уравнения
Риккати:
![]()
- Уравнения Якоби:
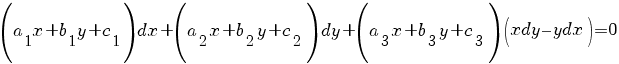
-
Уравнения
в полных дифференциалах
:
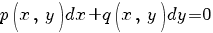
-
Уравнения
Клеро:
![]()
-
Уравнения
Лагранжа:
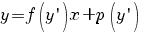
-
Уравнения,
приводящиеся к уравнению Бернулли:
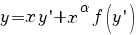 ,
,
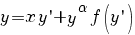
Решением (интегралом) д\у порядка n называется функция y(x), имеющая на
некотором
интервале (a,
b) производные
![]() до
порядка n включительно
и удовлетворяющая этому уравнению.
до
порядка n включительно
и удовлетворяющая этому уравнению.
Общий интеграл дифференциального уравнения — это общее решение, которое имеет неявный вид Ф(x,y,C1,C2,C3,...Cn) = 0.
Интегральной
кривой называется график решения
геометрически неопределённого интеграла (первообразной),
представляющего собой семейство
«параллельных» кривых ![]() ,
где каждому числу С соответствует
определенная кривая семейства. График
каждой кривой и называется интегральной
кривой.
,
где каждому числу С соответствует
определенная кривая семейства. График
каждой кривой и называется интегральной
кривой.
Задача Коши. Существование и единственность решений уравнений n-го порядка и систем уравнений.
Задача Коши, x0, y0 - начальные данные:
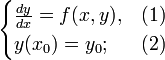
Решением задачи Коши является функция, определённая на интервале <a,b>, включающем x0, являющаяся решением уравнения (1) и удовлетворяющая начальному условию (2).
Определение. Решением интегрального уравнения:
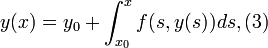 ,является
функция
,является
функция ![]() ,
которая определена на <a,b> принадлежит
x0 и
,
которая определена на <a,b> принадлежит
x0 и
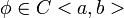 (непрерывна)
(непрерывна)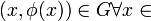 <a,b>
<a,b>подстановка превращает уравнение (3) в тождество.
Лемма. Функция является решением задачи Коши тогда и только тогда, когда она является решением интегрального уравнения.
Теорема: Существует единственное решения ДУ n-го порядка
yn= f (x, y, y’, y’’ , … y(n-1))удовлетворяющее условию: y (x0) = y0, y’ (x0) = y0`, y``( x0)= y0 ‘’ , … , y(n-1) (x0) = y0(n-1)
Если в окрестности нач. знач. ( , , y``0, … , y0(n-1))
Функция f является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица по всем аргументам начиная со второго .
Теорема: Существование и единственности решения системы :
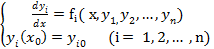 (3.9)
(3.9)
Предположим , что в области D , определённой неравенствами:
x0
– a
<=
x
<=
x0
+ a
i
= (1, 2, … ,![]() )
)
![]() –
–![]()
правые части уравнения (3.9) удовлетворяют условиям :
Все ф-ции
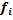 (x,
(x,
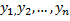 )-
непрерывны, сл-но и ограничены. i=
(1, 2, … , n)
│fi│
)-
непрерывны, сл-но и ограничены. i=
(1, 2, … , n)
│fi│
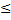 M
MВсе ф-ции (x, ) удовлетворяет условию Липшица
![]()
Уравнения вида , .
Некоторое уравнение путем подходящей замены переменных, можно привести к уравнению с разделенными переменными.
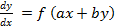 , где а и b
–постоянные числа , которые заменой
z
= ax
+ by
приводят к уравнению с разделенными
переменными.
, где а и b
–постоянные числа , которые заменой
z
= ax
+ by
приводят к уравнению с разделенными
переменными.
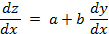 ;
;
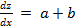 f
(z)
f
(z)
![]() ;
;
 =
dx;
x
=
=
dx;
x
= ![]() + C
Напомним, что функция Ф(x
, y)
называется
однородной степени k,
если выполняется следующее неравенство
Ф (tx , ty ) =
+ C
Напомним, что функция Ф(x
, y)
называется
однородной степени k,
если выполняется следующее неравенство
Ф (tx , ty ) = ![]() Ф
(x
, y)
Ф
(x
, y)
Правая
часть однородного уравнения является
однородной функцией х и у нулевой степени
однородности, поэтому уравнение вида
M
(x,
y)
dx
+ N
(x
,y)
dy
= 0 будет однородным, если M(x
, y)
и N
(x
, y)
является однородными функциями x
, y
одинаковой степени однородности, то
есть в этом случае 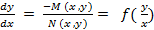 .
.
Уравнение
вида
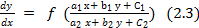 преобразуется в однородное уравнение
путем переноса из начала координат в
точку пересечения с координатами
(x1,y1)
прямых
преобразуется в однородное уравнение
путем переноса из начала координат в
точку пересечения с координатами
(x1,y1)
прямых 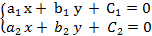
Действительно в новых координатах
x = x – x1
y = y – y1
Свободный
член в уравнениях этих прямых будет
равен 0, коэффициенты при текущих
координатах остаются неизменными, а
производная 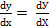
и
уравнение преобразуется к виду 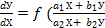 )
или
)
или 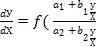 )
=
)
= ![]() (
(![]() ,
является однородным уравнением.
,
является однородным уравнением.
Этот
метод не применим, только если прямые
a1x
+ b1y
+ c1
= 0 a2x
+ b2y
+ c2
= 0 параллельны, но в этом случае a1=
кa2
b2=
kb1
и уравнение может быть записано в виде
![]() f
(
f
(![]() которое, как и ранее с заменой , z=
которое, как и ранее с заменой , z=
![]() , преобразованное уравнение с
разделёнными переменными .
, преобразованное уравнение с
разделёнными переменными .
