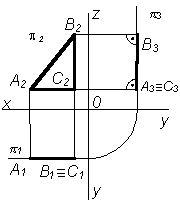12

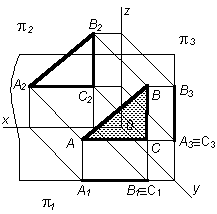
21Плоскости уровня

Плоскостью частного положения называют плоскость, которая либо перпендикулярна, либо параллельна одной из плоскостей проекций. Плоскости частного положения могут быть проецирующими плоскостями и плоскостями уровня

Характеристика	Наглядное изображение	Эпюр
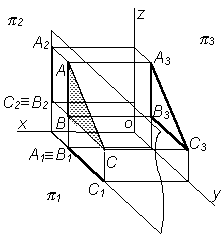
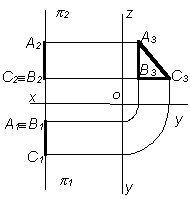
Фронтальная плоскость – это плоскость, параллельная плоскости 2. Эта плоскость пересекает плоскость 1 параллельно оси ОХ, а плоскость 3 – по линии, параллельной оси OZ
Горизонтальная плоскость – это плоскость, параллельная плоскости проекции 1. Эта плоскость пересекает плоскость 2 параллельно оси ОХ, а плоскость 3 – параллельно оси ОУ
Профильная плоскость – это плоскость, параллельная плоскости 3. Эта плоскость пересекает плоскости проекций 1 и 2 по линиям, параллельным оси Z

Таким образом, если плоскость параллельна какой-либо плоскости проекций, то на эту плоскость она проецируется в натуральную величину, а две ее другие проекции есть прямые линии параллельные осям проекций.

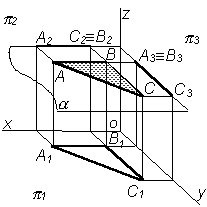
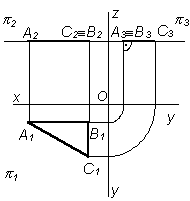
16 . Две плоскости в пространстве могут располагаться параллельно или пересекаться. В частном случае пересекающиеся плоскости могут быть взаимно перпендикулярными.

Плоскости пересекающиеся

Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии.

Вербальная форма	Графическая форма
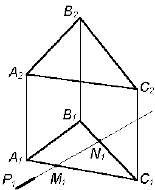
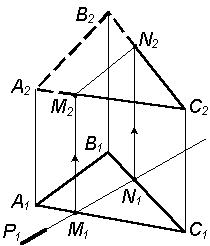
1. Для построения линии пересечения двух плоскостей Р(Р1) и Q( АВС) необходимо определить две точки M и N – общие для этих плоскостей. Видно, что горизонтальная проекция плоскости Р1 совпадает с горизонтальной проекцией линии пересечения плоскостей Р и Q. M1N1 = P1 Q1
3. Определяем видимость. Часть плоскости Q ( АВС) не видима, так как она расположена за плоскостью Р

2 Взаимное положение прямых в пространстве

Две прямые в пространстве могут иметь различное расположение:

• пересекаться (лежать в одной плоскости). Частный случай пересечения – под прямым углом;

• могут быть параллельными (лежать в одной плоскости);

• совпадать – частный случай параллельности;

• скрещиваться (лежать в разных плоскостях и не пересекаться).

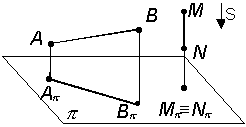
3Если точка лежит на прямой, то ее проекция располагается на соответствующей проекции этой же прямой А m А_ m_ (рис. 1.11).

Рис. 1.10 или		Рис. 1.11
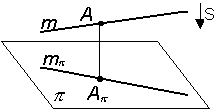
Рис. 3.4	Точка принадлежит прямой, если их одноименные проекции совпадают (рис. 3.4). Точка С принадлежит отрезку АВ, так как С2 принадлежит фронтальной проекции отрезка, а С1 – горизонтальной проекции отрезка.

6. Прямые уровня

Всякую линию, параллельную плоскости проекций, называют линией уровня. В начертательной геометрии различают три основные линии уровня: горизонталь, фронталь и профильную линии (табл. 3.1).