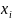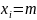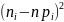Задача 10.18
Имеются следующие данные о качестве детского питания, изготовленного различными фирмами (в баллах): 40, 39, 42, 37, 38, 43, 45, 41, 48. Есть основание полагать, что показатель качества продукции последней фирмы (48) зарегистрирован неверно. Является ли это значение аномальным (резко выделяющимся) на 5%-ном уровне значимости?
Решение
Проверяемая гипотеза Но: х0 = у0, т.е. средние выработки рабочих одинаковы по новой и старой технологиям. В качестве конкурирующей гипотезы можно взять Н1- Хо>Уо или Р2: хо≠уо (в данной задаче более естественна гипотеза Н1, так как ее справедливость означает эффективность применения новой технологии).
фактическое значение статистики критерия t =85-78/ = 4.00
При конкурирующей гипотезе Н1 критическое значение статистики находится из условия т. е. Ф(Tкр) = 1 – 2 * 0.05 = 0.9, откуда по табл. II приложений Tkр = T0,9 = 1>64, а при конкурирующей гипотезе H2 — из условия, т.е. Ф(Tkp)= 1-0,05 = 0,95, откуда
по таблице Tkр=Tо,95==1,96. Так как фактически наблюдаемое значение t = 4,00 больше
Будем теперь предполагать, что распределение признака случайной величины) X и Y в, не только для больших, но и для малых по объему выборок. Если же дисперсии а2 и а2 неизвестны, но равны, т.е. , то в качестве неизвестной величины а2 можно взять ее оценку — «исправленную» выборочную дисперсию Однако «лучшей» оценкой для а2 будет дисперсия «смешанной» совокупности объема n1+n2, т.е.
а оценкой дисперсии разности независимых выборочных
средних - . имеет t-распределение Стьюдента с кг=п\+П2—2 степенями свободы. Поэтому критическое значение статистики t находится по тем же формулам в зависимости от типа критической области, в которых вместо функции Лапласа ф(t) берется функция Q(t,k) для распределения Стьюдента при числе степеней свободы k=n1+n2-2, т.е. Q(t,k) = 1-2а или Q(t,k) = 1-a. При этом сохраняется то же правило опровержения (принятия) гипотезы: гипотеза Щ отвергается на уровне значимости а, если |t| > (в случае односторонней критической области), либо если |t| > (в случае двусторонней критической области); в противном случае гипотеза Ho не отвергается (принимается).
Ответ:
Значение
х9 = 48 является аномальным, так как t =
2,95 >
=
1,89 (односторонний критерий).
Задача 10.19
Вступительный
экзамен проводился на двух факультетах
института. На финансово-кредитном
факультете из n1=900 абитуриентов выдержали
экзамен m1=500 человек; а на учетно-статистическом
факультете из n2=800
абитуриентов — m2=408. На уровне значимости
а= 0,05 проверить гипотезу об отсутствии
существенных различий в уровне подготовки
абитуриентов двух факультетов. Рассмотреть
два случая: а) конкурирующая гипотеза
Н1:р1
р2\
б) конкурирующая гипотеза Н2: p1>p2.
Решение
Проверяемая гипотеза Но: х0 = у0, т.е. средние выработки рабочих одинаковы по новой и старой технологиям. В качестве конкурирующей гипотезы можно взять Н1- Хо>Уо или Р2: хо≠уо (в данной задаче более естественна гипотеза Н1, так как ее справедливость означает эффективность применения новой технологии).
фактическое значение статистики критерия t =85-78/ = 4.00
При конкурирующей гипотезе Н1 критическое значение статистики находится из условия т. е. Ф(Tкр) = 1 – 2 * 0.05 = 0.9, откуда по табл. II приложений Tkр = T0,9 = 1>64, а при конкурирующей гипотезе H2 — из условия, т.е. Ф(Tkp)= 1-0,05 = 0,95, откуда
по таблице Tkр=Tо,95==1,96. Так как фактически наблюдаемое значение t = 4,00 больше
Будем теперь предполагать, что распределение признака случайной величины) X и Y в, не только для больших, но и для малых по объему выборок. Если же дисперсии а2 и а2 неизвестны, но равны, т.е. , то в качестве неизвестной величины а2 можно взять ее оценку — «исправленную» выборочную дисперсию Однако «лучшей» оценкой для а2 будет дисперсия «смешанной» совокупности объема n1+n2, т.е.
а оценкой дисперсии разности независимых выборочных
средних - . имеет t-распределение Стьюдента с кг=п\+П2—2 степенями свободы. Поэтому критическое значение статистики t находится по тем же формулам в зависимости от типа критической области, в которых вместо функции Лапласа ф(t) берется функция Q(t,k) для распределения Стьюдента при числе степеней свободы k=n1+n2-2, т.е. Q(t,k) = 1-2а или Q(t,k) = 1-a. При этом сохраняется то же правило опровержения (принятия) гипотезы: гипотеза Щ отвергается на уровне значимости а, если |t| > (в случае односторонней критической области), либо если |t| > (в случае двусторонней критической области); в противном случае гипотеза Ho не отвергается (принимается).
10.20
|
A |
B |
C |
D |
X |
30 |
52 |
21 |
74 |
N |
300 |
400 |
250 |
500 |
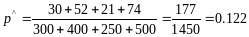
Выборочные доли делалей:
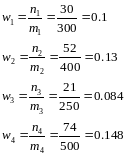
По
таблице V
Ответ:
Так как
,
то гипотезу
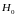отвергаем тоесть различие существенно.
10.21
По старой методике:
X |
303 |
307 |
308 |
Всего |
N |
1 |
4 |
4 |
9 |
По новой методике:
X |
303 |
304 |
306 |
308 |
Всего |
N |
2 |
6 |
4 |
1 |
13 |
А)
Б)
Найдем выборочную дисперсию по данным выборки:
Найдем выборочные средние:
Выборочная дисперсия:
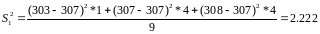
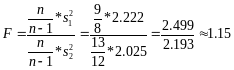
A)
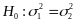Конкурирующая
гипотеза
По
таблице VI
Ответ:
Так
как
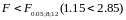,то
гипотезу
не отвергаем, различие не существенно.
Б)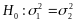
Конкурирующая
гипотеза
По
таблице VI
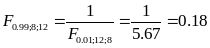
Ответ:
Поскольку
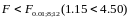и
то гипотеза
не отвергается.
Существенных различий нет.
10.22
Нулевая
гипотеза
Найдем исправленные выборочные дисперсии:
Найдем среднюю арифметическую дисперсию :
По
таблице VI
Ответ:
Поскольку
,
то гипотезу
не отвергаем, различие не существенно.
Первый способ существенно лучшим
признать нельзя.
10.23
Гипотезы:
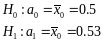
A)
Используем критерий Стьюдента:
По
таблице IV
Ответ:
Поскольку
,
то отклонение не случайно.
Б)
Так
как
то критическая область правосторонняя
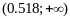
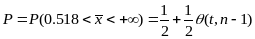
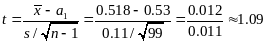
Используем таблицу IV
Ответ:
10.24
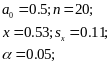
Гипотезы:
A)
Используем критерий Стьюдента:
По
таблице IV
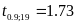
Ответ:
Поскольку
,
то отклонение можно считать случайным.
Б)
Так как то критическая область правосторонняя
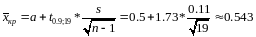
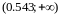
Используем таблицу IV
Ответ:
Ответ:
Существенных различий нет, так как:
а) t = 1,88 < = 1,96 (двусторонний критерий);
б) t = 1,88 < = 1,64 (односторонний критерий).
10.28
xi |
x_i+1 |
ni |
x*i |
(x - x_ср)^2 |
z_i |
0 |
500 |
58 |
250 |
1968409 |
-inf |
500 |
1000 |
96 |
750 |
815409 |
-1,72 |
1000 |
1500 |
239 |
1250 |
162409 |
-0,98 |
1500 |
2000 |
328 |
1750 |
9409 |
-0,22 |
2000 |
2500 |
147 |
2250 |
356409 |
0,51 |
2500 |
3000 |
132 |
2750 |
1203409 |
1,26 |
z_(i+1) |
Ф(zi) |
Ф(zi+1) |
n'i |
-1,72 |
-0,5 |
-0,4573 |
42,7 |
-0,98 |
-0,4573 |
-0,334 |
123,6 |
-0,22 |
-0,334 |
-0,0871 |
246,9 |
0,51 |
-0,0871 |
0,195 |
282,1 |
1,26 |
0,195 |
0,3962 |
201,2 |
inf |
0,3962 |
0,5 |
103,8 |
|
|
|
|
x_среднее = 1653
Дисперсия: 445591
Среднеквадрическое отколонение: 667, 526
s = 6
alpha = 0,05
x_кр = 5,99
x_набл = 2,37
5,99 > 2,37
лямбда = 0,35
лямбда от 0,05 = 1,36
0,35 < 1,36
Ответ: Гипотеза не отвергается.
10.29
x_i |
x_i+1 |
n |
x*i |
(x - x_ср)^2 |
1 |
4 |
6 |
5 |
112,36 |
2 |
6 |
8 |
7 |
73,96 |
3 |
8 |
10 |
9 |
43,56 |
4 |
10 |
12 |
11 |
21,16 |
5 |
12 |
14 |
13 |
6,76 |
6 |
14 |
16 |
15 |
0,36 |
7 |
16 |
18 |
17 |
1,96 |
8 |
18 |
20 |
19 |
11,56 |
9 |
20 |
22 |
21 |
29,16 |
10 |
22 |
24 |
23 |
54,76 |
11 |
24 |
26 |
25 |
88,36 |
zi |
zi+1 |
Ф(zi) |
Ф(zi+1) |
n'i |
-inf |
-2,202 |
-0,5 |
-0,4793 |
2,17 |
-2,202 |
-1,74 |
-0,4793 |
-0,4591 |
1,92 |
-1,74 |
-1,28 |
-0,4591 |
-0,3997 |
5,94 |
-1,28 |
-0,82 |
-0,3997 |
-0,2939 |
10,58 |
-0,82 |
-0,36 |
-0,2939 |
-0,1406 |
15,33 |
-0,36 |
0,091 |
-0,1406 |
0,0359 |
17,65 |
0,091 |
0,55 |
0,0359 |
0,2088 |
17,29 |
0,55 |
1,009 |
0,2088 |
0,3413 |
13,25 |
1,009 |
1,46 |
0,3413 |
0,4279 |
8,66 |
1,46 |
1,92 |
0,4279 |
0,4726 |
4,47 |
1,92 |
inf |
0,4726 |
0,5 |
2,24 |
x_среднее = 15,6
Дисперсия: 19
Среднеквадрическое отколонение: 4,35
s = 11
k = 10
alpha = 0,05
x_кр = 18,3
x_набл = 1,47
18,3 > 1,47
лямбда = 0,3
лямбда от 0,05 = 1,36
0,3 < 1,36
Ответ: Гипотеза не отвергается.
10.31. На
уровне значимости 0,05 проверить гипотезу
о показательном законе распределения
признака (случайной величины) Х используя
критерий
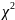– Пирсона
Время безотказной работы |
0--5 |
5--10 |
10--15 |
15--20 |
20--25 |
25--30 |
Число устройств |
133 |
45 |
15 |
4 |
2 |
1 |
Распределение 200 элементов.
Решение.
Вычислим выборочную среднюю:
Найдем оценку параметра предполагаемого показательного распределения:
Таким образом, функция предполагаемого показательного распределения имеет вид:
Найдем вероятность попадания Х в каждый из интервалов по формуле:
Для интервалов:
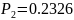
Найдем теоритические частоты:
Где
– вероятность попадания в i-й интервал.
Для всех интервалов:
Сравним эмпирические и теоритические частоты с помощью критерия Пирсона. Составив таблицу, и объединив малочисленные частоты (4+2+1=7) и соответствующие им теоритические частоты (6.30+2.32+0.84=9.46).
|
|
|
|
|
|
1 |
133 |
126.42 |
406.6 |
43.2964 |
0.3425 |
2 |
45 |
46.52 |
365.9 |
2.3104 |
0.0497 |
3 |
15 |
17.10 |
164.7 |
4.4100 |
0.2579 |
4 |
7 |
9.46 |
49.4 |
6.0516 |
0.6397 |
∑ |
n=200 |
|
|
|
|
Было объединено в один интервал (15,30) в виду малочисленности частот.
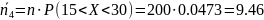
По таблице
критических точек распределения
,
по уровню значимости α=0.05 и числу степеней
свободы
находим критическую точку правосторонней
критической области
.
Так
как
нет оснований отвергать гипотезу.
10.34. Имеются следующие данные о засоренности партии семян клевера семенами сорняков:
Число семян в оной пробе
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
∑ |
Число проб |
405 |
366 |
175 |
40 |
8 |
4 |
2 |
1000 |
На уровне значимости α=0.05 проверить гипотезу о том, что случайная величина Х – число семян сорняков – распределена по закону Пуассона, используя критерий:
а) – Пирсона; б) Коломогорова.
Решение. Вычислим выборочную среднюю:
В качестве неизвестного параметра λ, берем его несмещенную и состоятельную оценку по выборке – выборочную среднюю:
Найдем вероятности значений случайной величины X:
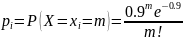
Для определения статистики составим таблицу:
|
|
|
|
|
|
|
|||||
1 |
0 |
405 |
0.4066 |
406.6 |
2.56 |
0.006 |
|||||
2 |
1 |
366 |
0.3659 |
365.9 |
0.01 |
0.0 |
|||||
3 |
2 |
175 |
0.1647 |
164.7 |
106.09 |
0.644 |
|||||
4 |
3 |
40 |
0.0494 |
49.4 |
88.36 |
1.789 |
|||||
5 |
4 |
8 |
0.0111 |
11.1 |
9.61 |
0.866 |
|||||
6 |
5 |
4 |
0.002 |
2.0 |
13.69 |
5.95 |
|||||
7 |
6 |
2 |
0.0003 |
0.3 |
|
|
|||||
∑ |
1000 |
1.0 |
1000 |
- |
|
||||||
При расчете объединяем два последних интервала, т.к. их частоты меньше 5.
Так как
новое число интервалов (с учетом
объединения двух последних)
,
а закон Пуассона определяется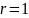
параметром, то число степеней свободы
.
По таблице
.
Так как
,
то гипотеза
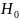согласуется с опытными данными.