Завдання на доп-бали з терії імовірності

Виконав:

Єфімов Дмитро

ІС-24

Київ 2014

10.15

По выборкам объемом n1=14 n2=9, найдены средние размеры деталей, соответственно х=182 у=185мм, изготовленных на первом и втором автоматах. Установлено, что размер детали, изготовленный каждым автоматом, имеет нормальный закон распределения. Известны дисперсии для первого второго автоматов. На уровне значимости 0.05 выявить влияние на средний размер детали автомата, на котором она изготовлена. Рассмотреть два случая:

А) конкурирующая гипотеза H1: Xo ≠ Yo б) конкурирующая гипотеза H1: Xo < Yo

Решение

Проверяемая гипотеза Но: х0 = у0, т.е. средние выработки рабочих одинаковы по новой и старой технологиям. В качестве конкурирующей гипотезы можно взять Н1- Хо>Уо или Р2: хо≠уо (в данной задаче более естественна гипотеза Н1, так как ее справедливость означает эффективность применения новой технологии).

фактическое значение статистики критерия t =85-78/ = 4.00

При конкурирующей гипотезе Н1 критическое значение статистики находится из условия т. е. Ф(Tкр) = 1 – 2 * 0.05 = 0.9, откуда по табл. II приложений Tkр = T0,9 = 1>64, а при конкурирующей гипотезе H2 — из условия, т.е. Ф(Tkp)= 1-0,05 = 0,95, откуда

по таблице Tkр=Tо,95==1,96. Так как фактически наблюдаемое значение t = 4,00 больше

критического значения Tkp (при любой из взятых конкурирующих гипотез), то гипотеза Щ отвергается, т.е. на 5%-ном уровне значимости можно сделать вывод, что новая технология позволяет повысить среднюю выработку рабочих.

Будем теперь предполагать, что распределение признака случайной величины) X и Y в каждой совокупности имеет нормальный закон. В этом случае, если дисперсии а2 и а2 известны, то проверка гипотезы проводится так же, как описано выше, не только для больших, но и для малых по объему выборок. Если же дисперсии а2 и а2 неизвестны, но равны, т.е. , то в качестве неизвестной величины а2 можно взять ее оценку — «исправленную» выборочную дисперсию Однако «лучшей» оценкой для а2 будет дисперсия «смешанной» совокупности объема n1+n2, т.е.

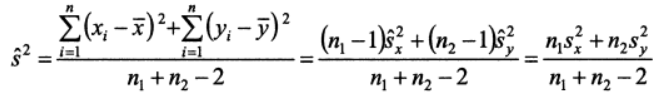
а оценкой дисперсии разности независимых выборочных

средних 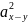- 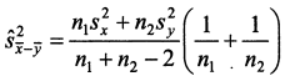. имеет t-распределение Стьюдента с кг=п\+П2—2 степенями свободы. Поэтому критическое значение статистики t находится по тем же формулам в зависимости от типа критической области, в которых вместо функции Лапласа ф(t) берется функция Q(t,k) для распределения Стьюдента при числе степеней свободы k=n1+n2-2, т.е. Q(t,k) = 1-2а или Q(t,k) = 1-a. 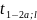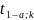При этом сохраняется то же правило опровержения (принятия) гипотезы: гипотеза Щ отвергается на уровне значимости а, если |t| > (в случае односторонней критической области), либо если |t| > (в случае двусторонней критической области); в противном случае гипотеза Ho не отвергается (принимается).

Ответ:

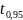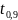а) Влияние существенно, так как t = 2,82 > = 1,96 (двусторонний критерий); б) влияние существенно, так как t=2,82 > =1,64 (односторонний критерий).

10.16

Расход сырья на единицу продукции составил:

Xi	303	307	308	Всего
Ni	1	4	4	9

По старой технологии.

Xi	303	304	306	308	Всего
Ni	2	6	4	1	13

По новой технологии

Полагая, что расходы сырья по каждой технологии имеют нормальные распределения с одинаковыми дисперсиями, на уровне значимости 0,05 выяснить дает ли новая технология экономию в среднем расходе сырья.