12. Модель Ферми-газа

Простейшей моделью независимых частиц для ядра является модель ферми-газа. Предельно упрощенный вариант оболочечной модели, в котором нуклоны трактуются как идеальный ферми-газ, заключенный внутри большого (в пределе неограниченного) объема. Область применимости: простое качественное объяснение некоторых общих свойств ядра, таких как насыщение ядерных сил, существование большой энергии симметрии и др.

В этой модели вместо сложной картины, являющейся суперпозицией индивидуальных нуклон-нуклонных взаимодействий, рассматривается движение не взаимодейству-ющих между собой нуклонов в поле усредненной потенциальной ямы с шириной R = r₀A^1/3. Глубину ямы U₀, при которой она должна удерживать нуклоны в пределах радиуса ядра R, можно найти из следующего простого рассуждения.

Основному состоянию ядра соответствует наинизшее состояние ферми-газа при нулевой абсолютной температуре, когда все нижние состояния заполнены нуклонами (вырожденный ферми-газ). Полное число нейтронов:

где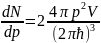 - плотность состояний в статистике Ферми (р - импульс нейтрона; V=4πR³/3=4πr₀A/3—объем ядра; р_макс—максимальный импульс, который может иметь нейтрон при заполнении состояний; двойка учитывает два направления спина).

В результате интегрирования имеем:

Д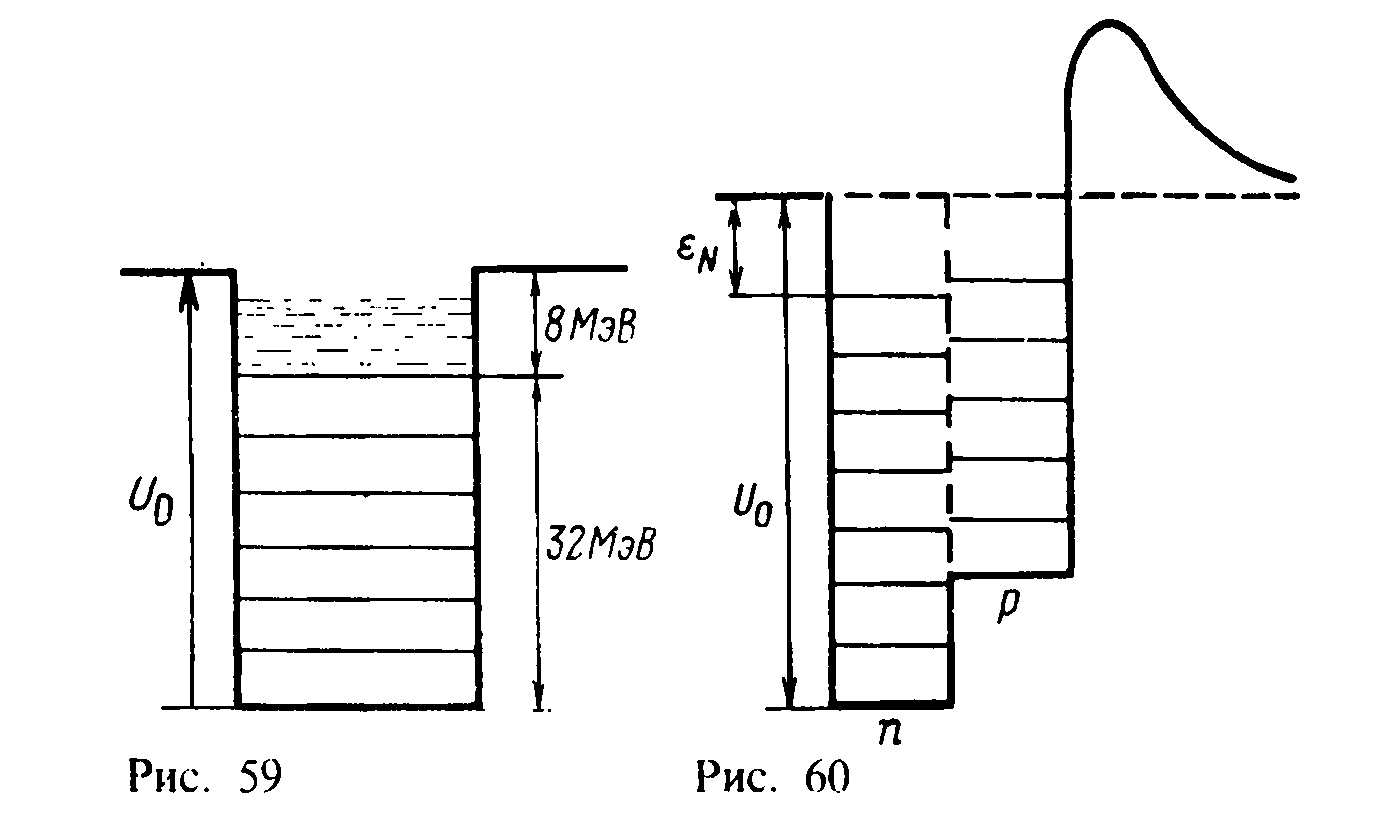 ля симметричного ядраN=A/2 и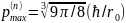 =1,3 10^-21 Дж с/см;

(для r₀ принято значение 1,2 10^-13 см).Отсюда максимальная кинетическая энергия нейтрона:

T_max=p²_max/2m_n =32 МэВ.

Так как средняя энергия связи нейтрона в ядре равна 8 МэВ, то глубина потенциальной ямы U₀=32 + 8 = 40 МэВ (рис. 59)., Такие же параметры имеет и протонная яма симметричного ядра. (Предполагается, что в случае симметричного, т. е. легкого, ядра кулоновским отталкиванием протонов можно пренебречь.) Если ядро несимметрично (N>Z), то T⁽ⁿ⁾_max>T^(p)_max и U⁽ⁿ⁾₀ >U^(p)₀ потому что между протонами существует дополнительное отталкивательное кулоновское взаимодействие (рис. 60, а также см. рис. 11 и 12 и текст к ним).

Нетрудно показать, что средняя энергия нуклонов в ядре

Оба полученных значения (U₀ и ) согласуются с аналогичными результатами, полученными из других предпосылок (см. § 82). Таким образом, модель независимых частиц дает неожиданно правдоподобное описание атомного ядра, которое оказалось похожим не только на жидкость, но и на газ.

Эту двойственную природу атомного ядра не следует считать противоречивой, потому что вырожденный ядерный ферми-газ сильно отличается от обычного ферми-газа при абсолютном нуле. В первом случае T_max≈ U₀, т.е. нуклоны ядра при столкновении с другими нуклонами практически не изменяют своего состояния. Они ведут себя как независимые частицы. Во втором случаеU₀ ≈ 10³T_max, т.е. «замороженные» частицы обычного газа связаны относительно гораздо сильнее, в результате чего обычный газ при абсолютном нуле проявляет свойства конденси-рованной среды.

Область применения модели ферми-газа не очень обширна. Она пригодна для качественного объяснения эффекта симметрии и насыщения, а также для объяснения свойств ядра, связанных с распределением внутриядерных нуклонов по импульсам. Последнее существенно при рассмотрении процессов, характеристики которых зависят от внутреннего движения нуклонов. Примером может служить процесс рождения π-мезонов при взаимодействии нуклона с ядром. Порог этой реакции существенно снижается при соударении внешнего нуклона с внутренним нуклоном ядра, движущимся навстречу внешнему.