6.Магнитный момент ядра и его экспериментальное определение

7.Квадрупольный момент и форма ядра

Простейшую модель квадруполя представляет пара равных и противоположно ориентированных диполей d, расположенных на некотором расстоянии ℓ (рис. 44, а). Такая система обладает квадрупольным моментом Q=2dℓ=2eδℓ. Так как квадрупольный момент Q пропорционален δи ℓ, то его значение (отнесенное к единичному заряду) измеряется в единицах площади.

К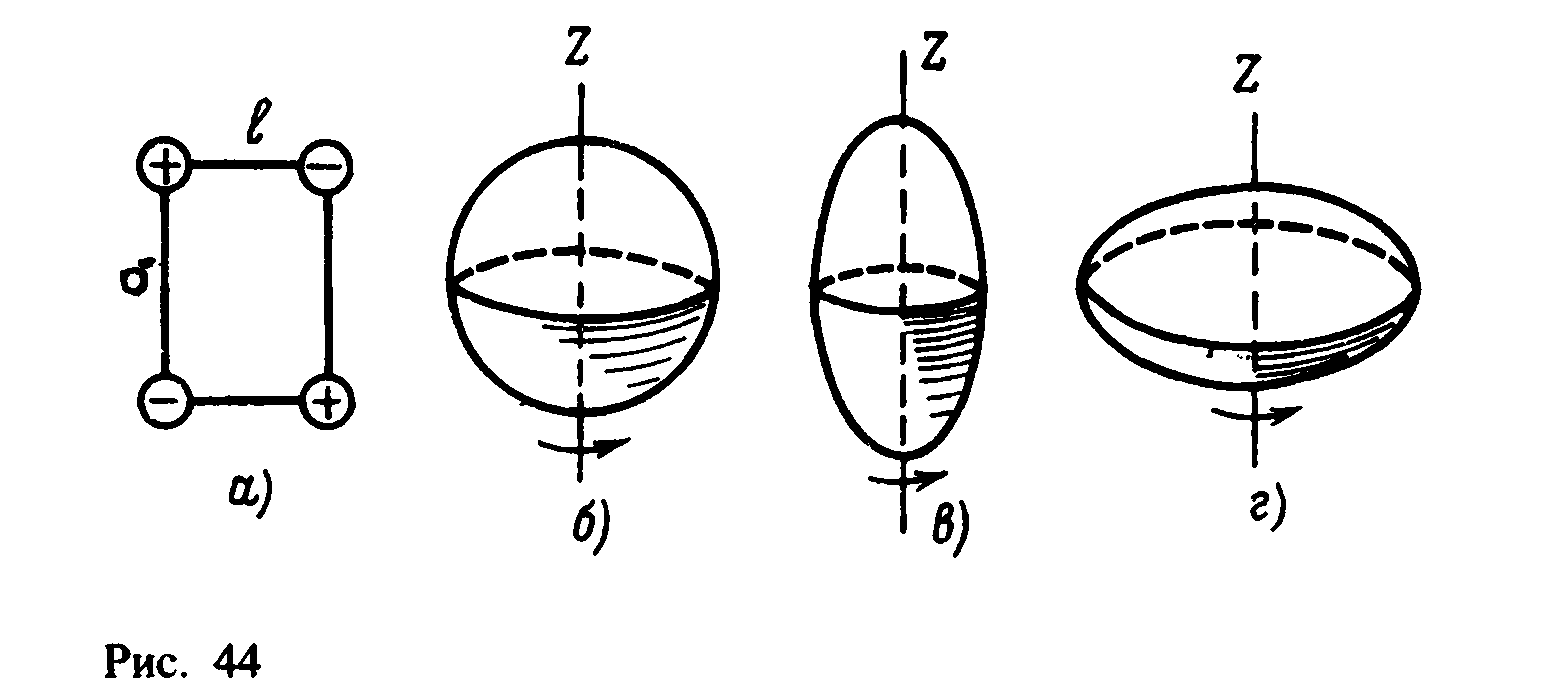 огда говорят о квадрупольном электрическом моменте ядра, то различают собственный (внутрен-ний) квадрупольный момент ядра Q₀ и наблюдаемый квадрупольный момент ядра Q. Собственный квадрупольный момент ядра Q₀ определяется как интеграл вида

Q₀=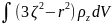 (7.8)

где r( ) - расстояние от центра инерции ядра; ζ— проекция r на ось ζ, совпадающую с осью симметрии ядра; ρ_z—плотность распределения заряда Z. Интегрирование ведется по всему объему ядра. Так как r² = ξ² + η² + ζ²,то 3ζ² = r² для сферически-симметричного распределения; 3ζ²>r² для распределения, вытянутого вдоль осиζ и 3ζ²<r² для сплюснутого распределения. Поэтому Q₀=0 для сферически-симметричного заряда (например, для магических ядер); Q₀>0 для распределения заряда, вытянутого вдоль оси ζ; Q₀<0 для сплюснутого (относительно оси ζ распределения заряда (рис. 44, б—г соответственно).

С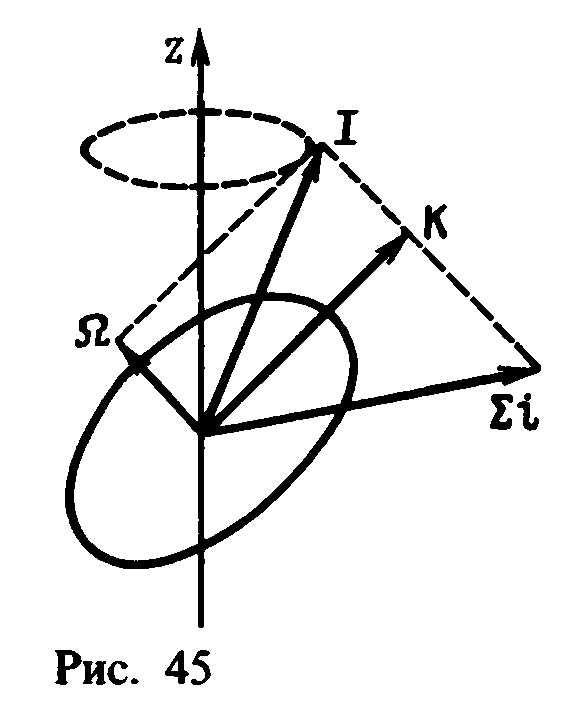 обственный квадрупольный момент Q₀ может быть определен из экспериментальных данных для сечения кулоновского возбуждения вращательных уровней ядер и вероятности γ-переходов между этими уровнями.

Наблюдаемый квадрупольный электрический момент Q определяется относительно оси z, совпадающей с выделенным направлением в пространстве:Q=

Его значение зависит от Q₀ и ориентации ядра относительно оси z. В свою очередь, ориентация ядра относительно оси z определяется ориентацией спина I относительно этой оси и его проекциейК на ось симметрии ядра. В общем случае спин I несферического ядра в возбужденном состоянии равен:I=К+Ω,(7.10)где К—проекция векторной суммы полных моментов нуклонов на ось симметрии ядра, а Ω—вращательный момент ядра какцелого(рис. 45).

Квантовомеханический подсчет, сделанный для максимально возможной проекции вектора I на ось z, дает следующую связь между Q, Q₀, I иК:

Q= Q₀ (7.11)

где выражение, стоящее перед Q₀, называется проектирующим множителем (Q является как бы проекцией Q₀ на ось z).

Из формулы (7.11) следует:

1) При Q₀≠Q наблюдаемый квадрупольный момент Q по абсолютному значению всегда меньше Q₀.

2) При I(I+1)>3К², т.е. при достаточно большихI, знак Q становится противопо-ложным знаку Q₀.

3) Для ядер в основном состоянии (Ω=0; I= К)Q= Q₀

Если I=0 (четно-четные ядра) или I=1/2, то Q=0 даже при Q₀≠0. При I≥1 наблюдаемый квадрупольный момент Q отличен от нуля. Отношение Q/Q₀ приближается к 1 при I>>1.

Q=~

4) Для четно-четных ядер в возбужденных состояниях К=0, но I=Ω≠0 иQ= - Q₀, еслиQ₀≠0.

Отличный от нуля квадрупольный момент Q можно обнаружить при помещении ядра в неоднородное электрическое поле Е, в котором возникает дополнительная энергия взаимодействия, пропорциональная Q. Так, в результате взаимодействия квадрупольного момента ядра с электрическим полем электронов возникают добавочные линии сверхтонкой структуры, которые не подчиняются правилу интервалов, справедливому для магнитного расщепления. Именно таким образом был обнаружен квадрупольный момент у дейтрона.