40. Резонансные реакции через составное ядро

Рассмотрим сечение образования составного ядра в районе изолированных уровней, т. е. когда ширины уровней Г меньше расстояний между ними. Изолированные уровни составного ядра отчетливо проявляются при взаимодействии медленных нейтронов с ядрами (рис. 9.6). На этом рисунке показано полное сечение реакции n+²³²Th для нейтронов с энергиями 120-210 эВ. То, что наблюдаемые резонансы - уровни составного ядра, следует из их ширины.

Ш ирины показанных на рис. 9.6 уровней (резонансов) после внесения поправок на аппаратную форму линии и доплеровское уширение оказываются 1 эВ. Это означает, что время жизни уровней τ= ħ/Г≥10^-15 с,что на 4 порядка превышает время пролета нейтрона с энергиями сотни эВ через ядро тория (это время≈ 10^-19 с).

Среднее расстояние между уровнями быстро уменьшается с ростом массового числа А и энергии возбуждения ядра. Все это приводит к тому, что с увеличением энергии нейтронов уровни начинают перекрываться. Для тяжелых ядер это происходит для нейтронов с энергией Е_n несколько кэВ. Энергия возбуждения составного ядра Е* при этом близка к энергии отделения нейтрона от этого ядра В_n, равной нескольким МэВ (Е* ≈В_n + Е_nи для медленных нейтронов Е_n В_n). Форма резонанса в ядерной физике та же, что и в физике частиц - брейт-вигнеровская. Формула Брейта - Вигнера без учета спинов частицы и ядра и их относительного орбитального момента имеет вид:

(9.20)

где = 𝜆_a/(2 ) - приведенная дебройлевская длина волны падающей частицы, а Еr- энергия резонанса.

Для сечения реакции рассеяния нейтронов в районе изолированного уровня формула (9.20) дает

(9.21)

В этих формулах Г/ħ- полная вероятность распада уровня составного ядра в единицу времени; Г_a/ħ, Г_b/ħ, Г_n/ħ - вероятности распада уровня составного ядра в единицу времени с вылетом частиц а, b и нейтрона. Сумма всех парциальных ширин Г_а, Г_b, Г_n… дает полную ширину уровня: Г = Г_а + Г_b + Г_n + ... .

При уходе от энергии резонанса Еr на ΔЕ=Г/2 в любую сторону сечение уменьшается в два раза. Таким образом, как и должно быть, Г - ширина уровня на половине высоты.

Из формулы Брейта—Вигнера, пользуясь соотношениями

[ Cечение реакции через составное ядро σ_ab можно записать в видеσ_ab = σ_acW_b,

где = σ_аС - сечение образования составного ядра частицей a,aW_b- вероятность его распада по каналу b (с вылетом частицы b).

Очевидно, = 1, где суммирование проводится по всем возможным конечным частицам.

С учетом того, что W_b = Г_b/Г, выражение, которое находится выше,можно записать в виде ]

можно получить сечение образования составного ядра σ_аC в области изолированного уровня:

откуда

При Е*=Еr сечения достигают максимумов. Эти максимальные значения следующие:

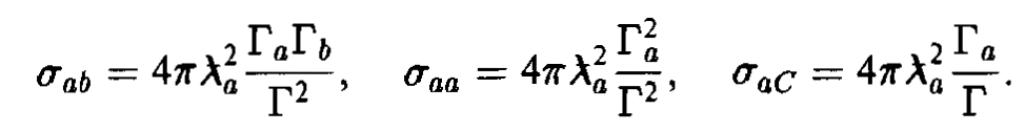
Отсюда видно, что величина сечения резонансной реакции, вызываемой частицей а, не может превышать величины .

41. Нерезонансные реакции через составное ядро

При больших энергиях возбуждения составного ядра (Е > 10 МэВ) его уровни перекрываются, и говорить об отдельных резонансах уже нельзя (см. в качестве примера рис. 9.7). Однако концепцию составного ядра можно сохранить и здесь. В результате усреднения по большому числу перекрывающихся резонансов сечение образования составного ядра в этой области приобретает достаточно плавную энергетическую зависимость (на рис. 9.7 для энергий нейтронов больше 5 МэВ). Получим эту зависимость, опираясь на простейшие предположения.

Предположим, что сечение не зависит от квантовых чисел налетающей частицы и ядра и что уровни составного ядра образуют непрерывный спектр. Пусть падающая частица является нейтральной и не нужно учитывать кулоновское взаимодействие, например, в случае образования составного ядра в реакциях с нейтроном. Вероятность образования составного ядра нейтроном определяется произведением вероятностей трех последовательных процессов:

1) попадания нейтрона в область пространства, где находится ядро (эффективное сечение этого процесса обозначим σ₀);

2) проникновения нейтрона внутрь ядра (вероятность этого процесса Р);

3) захвата ядром нейтрона (вероятность ξ).

С ечение процесса, состоящего в том, что частица попадает в область ядра с радиусом R, это не что иное, как его геометрическое сечение. Поэтому

σ₀=σ_геом= (9.25)

где - приведенная длина волны де Бройля нейтрона.

У прощенная зависимость потенциала, в котором движется нейтрон, от расстояния до центра ядра приведена на рис. 9.8. При r=R на границеядра происходит скачок потенциала, связанный с тем, что в области r< R действуют ядерные силы, имеющие характер притяжения. При прохождении плоской волны на границе потенциала возникает отраженная волна. Квантово-механический расчет проницаемости Р через скачок потенциала для частиц с массой m, кинетической энергией Е и орбитальным моментом ℓ=0 приводит к следующему результату:

где

В результате отражения на границе ядра нейтронной волны происходит потенциальное упругое рассеяние.

В модели составного ядра считается, что частица, попав в ядро, с вероятностью ξ= 1 остается в нем.

Таким образом, сечение образования составного ядра нейтроном определяется выражением

При высоких энергиях <<R и k ≈k₀. Поэтому и получаем для сечения образования составного ядра нейтроном

σ_nc≈πR²

Э то выражение применимо не только к нейтронам, но и другим высокоэнергичным, в том числе и заряженным, частицам (роль кулоновского барьера при достаточно больших энергиях становится несущественной). Таким образом, в рассматриваемой модели ядро при высоких энергияхполностью поглощает упавшие на него частицы и сечение их взаимодействия с ядром становится равным его геометрическому сечению. Такая модель называется моделью черного ядра.

Рассмотрим теперь область энергий составного ядра ниже первого резонанса (Е*< Е₁). В этой области энергий (рис. 9.10) сечение образования составного ядра нейтроном σ_nC не имеет особенностей и можно воспользоваться формулой (9.27). Рассматриваемая область - это область близких к нулю кинетических энергий нейтронов. Поэтому, полагая >>R и k₀>>k, получаем, что сечение образования составного ядра нейтроном при самых низких энергиях обратно пропорционально его скорости v_n:

Здесь использовано то, что

При больших энергиях возбуждения составного ядра, когда происходит перекрытие большого числа его уровней, невозможно описывать ядерную реакцию, учитывая влияние каждого уровня на процесс возбуждения и распада составного ядра. Концепцию составного ядра в этом случае дополняют статистическими соображениями. В результате получается статистическая теория ядерных реакций, или модель испарения.

Согласно модели испарения реакция протекает следующим образом. Попавшая в ядро частица быстро теряет энергию, передавая ее всем нуклонам ядра. Возникает термодинамически равновесное состояние ядра, т. е. ядро приобретает некоторую температуру (температура не возбужденного ядра равна нулю). Далее в течение некоторого времени (это и есть время жизни составного ядра) каждый нуклон имеет энергию, недостаточную для вылета, хотя ядро в целом сильно возбуждено. Наконец, в результате достаточно сильной флуктуации один из нуклонов приобретает необходимую для вылета энергию и испаряется из ядра. При этом распределение испущенных нуклонов по энергии имеет вид, сходный с максвелловским.