27. Последовательные и параллельные распады. Вековое уравнение

Если ядра N₂, возникающие в результате радиоактивного распада ядер N₁ в свою очередь являются радиоактивными, то для описания процесса этих двух последовательных превращений записывают систему двух дифференциальных уравнений: ; гдеλ₁ и λ₂ - постоянные распада ядер N₁ и N₂. Здесь первое дифференциальное уравнение описывает процесс радиоактивного распада первичного (материнского) вещества. Второе дифференциальное уравнение описывает изменение количества вторичного (дочернего) вещества и содержит справа два слагаемых. Первое дает прирост радиоактивных ядер вторичного вещества из-за распада первичного и поэтому в точности равно , т. е. числу распадающихся ядер первичного вещества. Второе слагаемое равно числу распадающихся ядер вторичного вещества.

Совершенно аналогично можно записать систему уравнений, описывающую взаимное превращение трех, четырех и т. д. веществ. Ниже рассмотрен только самый простой (но имеющий наибольшее практическое значение) случай двух веществ, опи-сываемый системой уравнений.

Решение этой системы уравнений в предположении, что Т₁>>Т₂( ) и N₂(0) = 0, приводит к следующему результату (для t<<T₁):

; (16.8)

Д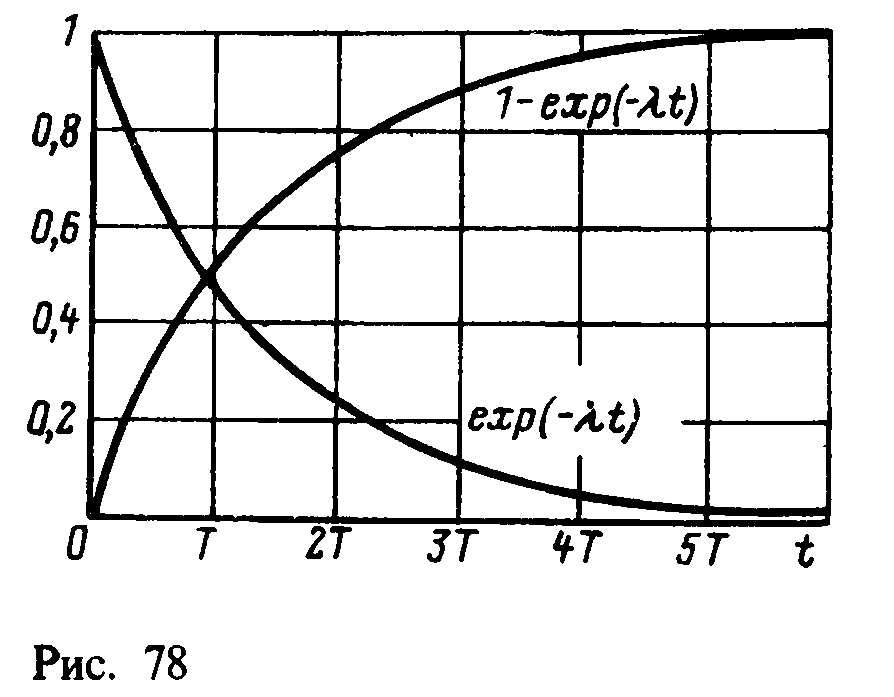 ля оценки значения N₂(t) можно использовать графический метод (рис. 78).

Соотношение (16.8) показывает, что количество радиоактивного дочернего вещества возрастает с течением времени и при t>>T₂( t>>1) приближается к своему предельному значению:

=const.

Обычно это условие записывается в форме и носит название векового.

28. Альфа-распад

α-Распад относится к числу ядерных процессов, происходящих под действием сильного взаимодействия. Поэтому для разрешенных α-переходов должны выполняться все известные законы сохранения, включая закон сохранения четности Р и закон сохранения изотопического спина Т.

Каждый из них накладывает определенные ограничения на разрешенные α-переходы. Так, из закона сохранения изотопического спина следует, что α-радиоактивное ядро (A, Z) и дочернее ядро (А-4, Z-2), образующееся после α-распада, должны иметь одинаковый изотопический спин Т (потому что изоспинα-частицыТ_а=0). Из закона сохранения четности Р и момента количества движения I следует, что четность и спин начального (Р_н и I_н) и конечного (Р_к и I_к) ядер должны быть связаны с орбитальным моментом а α-частицы ℓ_α соотношениями:

; Р_н/Р_к=(-1)^ℓα (17.5)

где все ℓ_α либо четные, либо нечетные числа. Напомним, что P_α=+1, а I_α=0. Остановимся более подробно на законах сохранения энергии и импульса.Условие энергетической возможности α-распада записывается следующим образом:

E_св = [М(A-4, Z-2) + M( ) - М(A, Z)]c²< 0 (17.6)

или

М(А, Z) >M(A-4, Z-2)+M( ).

Масса (энергия) исходного ядра должна быть больше суммы масс (энергий) ядра-продукта и α-частицы. Избыток энергии исходного ядра выделяется при α-распаде ядра в виде кинетической энергии

Q = [М(A, Z) – M(A-4, Z-2)-М( )]с² = Ta+Тяд (17.7)

которая распределяется между α-частицей и ядром-продуктом таким образом, чтобы выполнялся закон сохранения импульсаp_α + p_ЯД = p(A, Z).

Считая, что распадающееся ядро покоится, получаем | p_α |=| p_ЯД| откуда Т_яд=Т_аМ_а/М_яа илиЕ_a=Т_a+Т_яд=Т_а(1+М_а/М_яд); Т_а=Е_а

Таким образом, подавляющую часть кинетической энергии, выделяющейся при α-распаде, уносит α-частица, и лишь незначительная ее доля приходится на ядро-продукт.

α-распад происходит только на тяжелых ядрах с Z > 60.

Для четно-четных изотопов зависимость периода полураспада от энергии α-распада Q_a хорошо описывается эмпирическим законом Гейгера - Неттола

(7.2)

где А и В - константы, слабо зависящие от Z. Для нечетно-четных, четно-нечетных и нечетно-нечетных ядер общая тенденция сохраняется, но периоды полураспада в 2 - 1000 раз больше, чем для четно-четных ядер с теми же Z и Q_a.

Большинство вылетающих α-частиц имеет энергии Е_а = 2 - 9 МэВ. Испускаемые α-частицы, как правило, имеют определенные энергии, характерные для каждого ядра. В ряде случаев спектр вылетающих α-частиц имеет тонкую структуру, т. е. состоит из нескольких близких друг к другу по энергии групп α-частиц.

Для точного определения области значений А и Z ядер, для которых энергетически возможен α-распад, надо воспользоваться экспериментальными данными об энергиях связи. Из них видно,что α-распад становится возможным, начиная с A≈140. В областях А=140-150 и А ≈210 величина Q_a имеет отчетливые максимумы, которые объясняются в оболочечной модели ядра. Максимум при А=140-150 связан с заполнением нейтронной оболочки с магическим числом N=A-Z =82, а максимум при А≈210 связан с заполнением протонной оболочки при Z=82. Именно за счет такого оболочечного эффекта первая (редкоземельная) область α-активных ядер начинается с N= 84= 82 + 2, а тяжелые α-радиоактивные ядра становятся особенно многочисленными, начиная с Z=84.

П усть внутри ядра радиуса R двигается «готовая» α-частица. В те моменты, когда она оказывается на поверхности ядра, она имеет возможность покинуть его с вероятностью Р. Рассмотрим потенциал V(r), в котором движется α-частица (рис. 7.5). За пределами ядра (r>R) - это положительный потенциал кулоновского отталкивания. На границе ядра вступает в игру мощное притяжение, обусловленное ядерными силами, и потенциальная кривая резко уходит вниз. Образуется потенциальный барьер. Потенциал внутри ядра (r<R) отрицателен, и его можно считать примерно постоянным. Итак,

Максимальная высота кулоновского барьера V>>Е_а

Рассчитаем вероятность α-частице пройти сквозь такой барьер. Для этого необходимо решить стационарное уравнение Шрёдингера для частицы в центральном потенциале V(r):

, где (7.8)

- оператор кинетической энергии, а - лапласиан

Вместо μ_а нужно брать приведенную массу системы: , где М - масса конечного ядра, образующегося в результате α-распада. Тогда, представив радиальную волновую функцию частицы в виде:

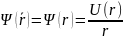
приходим к одномерному уравнению Шрёдингера:

. (7.9)

Для простоты рассмотрим случай прямоугольного барьера шириной d = R0-R (рис. 7.6).

У равнение (7.9) надо решить для областей 1, 2, 3. Пусть частица проходит барьер слева направо. Тогда искомое решение должно иметь вид распространя-ющейся вправо плоской волны Ae^ikr в области r>R₀ и суммы падающей на барьер и отраженной от барьера волн (падающие и отраженные частицы) в области r<R:

Здесь .

Внутри барьера (область 2) волновая функция имеет вид u(r) = Ce^qr + De^-qr, (7.11)

причем нефизическое решение Ce^qr, дающее растущую вероятность найти частицу по мере продвижения вглубь барьера, должно быть подавлено. Поэтому C/D ≈ 0.

Вероятность (коэффициент) прохождения через барьер Р есть отношение вероятностей обнаружить частицу в точках R₀ и R. Для этого достаточно знать волновую функцию u(r) в области барьера (область 2):

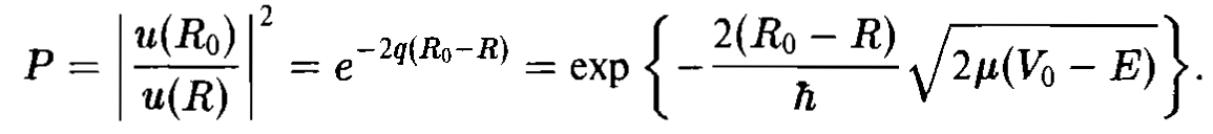
Для определения вероятности проникновения через барьер произвольной формы необходимо выполнить интегрирование

где пределами интегрирования являются границы барьера, т. е. той области, в которой кинетическая энергия отрицательна.

Для того чтобы рассчитать постоянную распада λ, надо коэффициент прохождения умножить, во-первых, на вероятность w_a того, что α-частица образовалась в ядре, и, во-вторых, на вероятность того, что она окажется на границе ядра. Грубую оценку этой последней вероятности можно получить, заметив, что если α-частица в ядре радиуса R имеет скорость v, то она будет подходить к границе в среднем v/(2R) раз в секунду. Отсюда для постоянной распада получаем выражение:

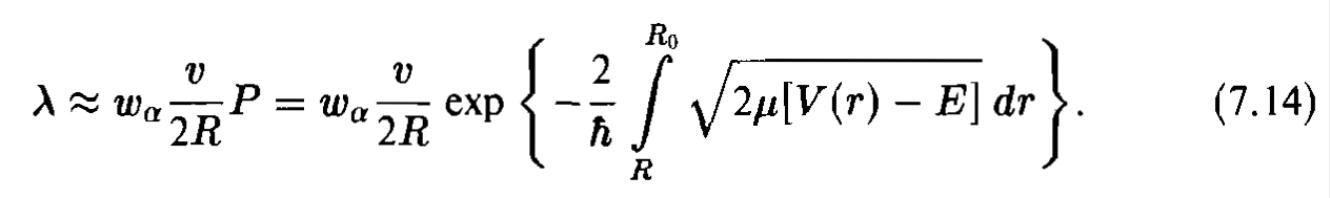
Из формулы (7.14) видно, что период полураспада сильно зависит от радиуса ядра, поскольку радиус R входит не только в предэкспоненциальный множитель, но и в показатель экспоненты, как предел интегрирования. Поэтому из данных по α-распаду можно довольно точно определять радиусы ядер. Полученные таким путем радиусы оказываются на 20-30% больше найденных в опытах по рассеянию электронов. Это различие связано с тем, что в опытах с быстрыми электронами измеряется радиус распределения электрического заряда в ядре, а в α-распаде измеряется то расстояние между центрами ядра и α-частицы, на котором перестают действовать ядерные силы.