8. Статистика и четность

Микрочастицы обладают своеобразной характеристикой, называемой статистикой. Статистика является не индивидуальным, а коллективным свойством. Она проявляется лишь в присутствии не менее чем двух одинаковых частиц. Существование статистики является следствием принципа неразличимости одинаковых микрочастиц и вероятностного характера описания состояния в квантовой теории.

Принцип неразличимости состоит в том, что любые две микрочастицы одного сорта, например два протона, абсолютно одинаковы по всем своим свойствам, т. е. принципиально неотличимы друг от друга. Такая абсолютная одинаковость свойственна только микрочастицам и совершенно невозможна в макроскопическом мире. Как бы мы ни старались, нам никогда не удастся, например, сделать два абсолютно одинаковых стальных шарика диаметром в 1 см.

Абсолютная неразличимость микрочастиц приводит к тому, что состояние из двух таких частиц по своим свойствам ничем не отличается от состояния, в котором эти частицы поменялись местами. Отсюда следует более сильное утверждение о том, что перестановка частиц одного сорта вообще не переводит систему в новое состояние. Согласно этому утверждению не существует состояния из двух одинаковых частиц, в котором первая частица находится в состоянии a, а вторая в состоянии b (или, наоборот, первая в состоянии b, вторая в состоянии a). Существует лишь состояние, в котором одна из частиц находится в состоянии а, а другая в состоянии b.

В квантовом мире, микрочастица не имеет траектории, а описывается волновой функцией, имеющей смысл амплитуды вероятности. Здесь нет возможности точно предсказать, в каких местах окажутся в определенный момент времени первая и вторая частицы, можно лишь рассчитать вероятность нахождения каждой из этих частиц в той или иной области пространства. Но если получится, что расчетная вероятность, попадания в счетчик равна 5% для первой частицы и 20% для второй, то для одинаковых частиц отношение этих вероятностей будет непроверяемой экспериментально. Поскольку частицы неразличимы, то мы сможем лишь установить, что вероятность зарегистрировать одну из частиц равна 25%. Таким образом в квантовом мире состояние системы из одинаковых частиц не изменяется при взаимных перестановках.

В квантовой теории состояние системы из nчастиц описывается волновой функцией Ψ_m1,…,mn(r₁,…,r_n), зависящей от координат r₁,...,r_n и проекций спинов m₁,...,m_n частиц. После перестановки двух частиц, например первой и второй, состояние системы должно остаться неизменным. Для этого нужно, чтобы волновая функция состояния с переставленными частицами совпадала с исходной с точностью до числового множителя, который мы обозначим через P₁₂:

Ψ_m2,m1,…,mn(r₂,…,r_n) = P₁₂ Ψ_m1,m2,…,mn(r₁,…,r_n) (2.42)

Произведя операцию перестановки первой и второй частиц дважды, мы придем к первоначальной функции. Отсюда следует, что Р₁₂² = 1, т. е. Р₁₂ = ±1. Аналогичное рассуждение может быть проведено для любой пары одинаковых частиц: при перестановке двух одинаковых частиц волновая функция либо остается неизменной, т. е. является симметричной по частицам, либо меняет знак, т. е. является антисимметричной по частицам.

Можно показать, что частицам определенного сорта всегда свойствен только один из этих двух возможных типов перестановочной симметрии. Такое свойство частиц по отношению к перестановкам и называется статистикой. Частицы подчиняются статистике Бозе-Эйнштейна, если волновая функция системы таких частиц симметрична по отношению к перестановке любой пары частиц:

Ψ_m1,m2,…,mn(r₁,…,r_n)= Ψ_m2,m1,…,mn(r₂,…,r_n) (2.43)

Соответствующие частицы называются бозе-частицами (бозонами).

Частицы подчиняются статистике Ферми-Дирака, если волновая функция системы таких частиц антисимметрична по отношению к перестановке любой пары частиц:

Ψ_m1,m2,…,mn(r₁,…,r_n)= -Ψ_m2,m1,…,mn(r₂,…,r_n) (2.44)

Соответствующие частицы называются ферми-частицами (фермионами).

Для частиц, подчиняющихся статистике Ферми-Дирака, справедлив принцип Паули, согласно которому в одном и том же состоянии может находиться неболее одной частицы. Из квантовой механики следует, что волновая функция двух разных частиц, находящихся соответственно в состояниях Ψ¹и Ψ², равна их произведению Ψ¹*Ψ². Для одинаковых частиц в соответствии с (2.44) произведение будет антисимметричным по частицам:

(2.45)

Но выражение (2.45), очевидно, обращается в нуль, если функции Ψ¹и Ψ² одинаковы, что и приводит к принципу Паули. Для двух бозонов вместо (2.45) получается симметризованная по частицам функция

(2.46)

Выражение (2.46) уже не обращается в нуль для одинаковых функций, так что в одном и том же состоянии может находиться любое количество одинаковых бозонов. Для бозе-частиц принцип Паули не выполняется.

Статистика Ферми-Дирака определяется как такая, в которой в каждом состоянии может находиться не более одной частицы, а статистика Бозе-Эйнштейна как такая, в которой в одном и том же состоянии может находиться любое число частиц. В отношении статистики Ферми-Дирака такое определение является полным. Однако для статистики Бозе-Эйнштейна такое определение недостаточно, так как в нем не отражен тот факт, что в этом случае запрещены состояния, антисимметричные по частицам. Т.е разрешенными оказываются только функции, четные относительно изменения знака относительной координаты

Д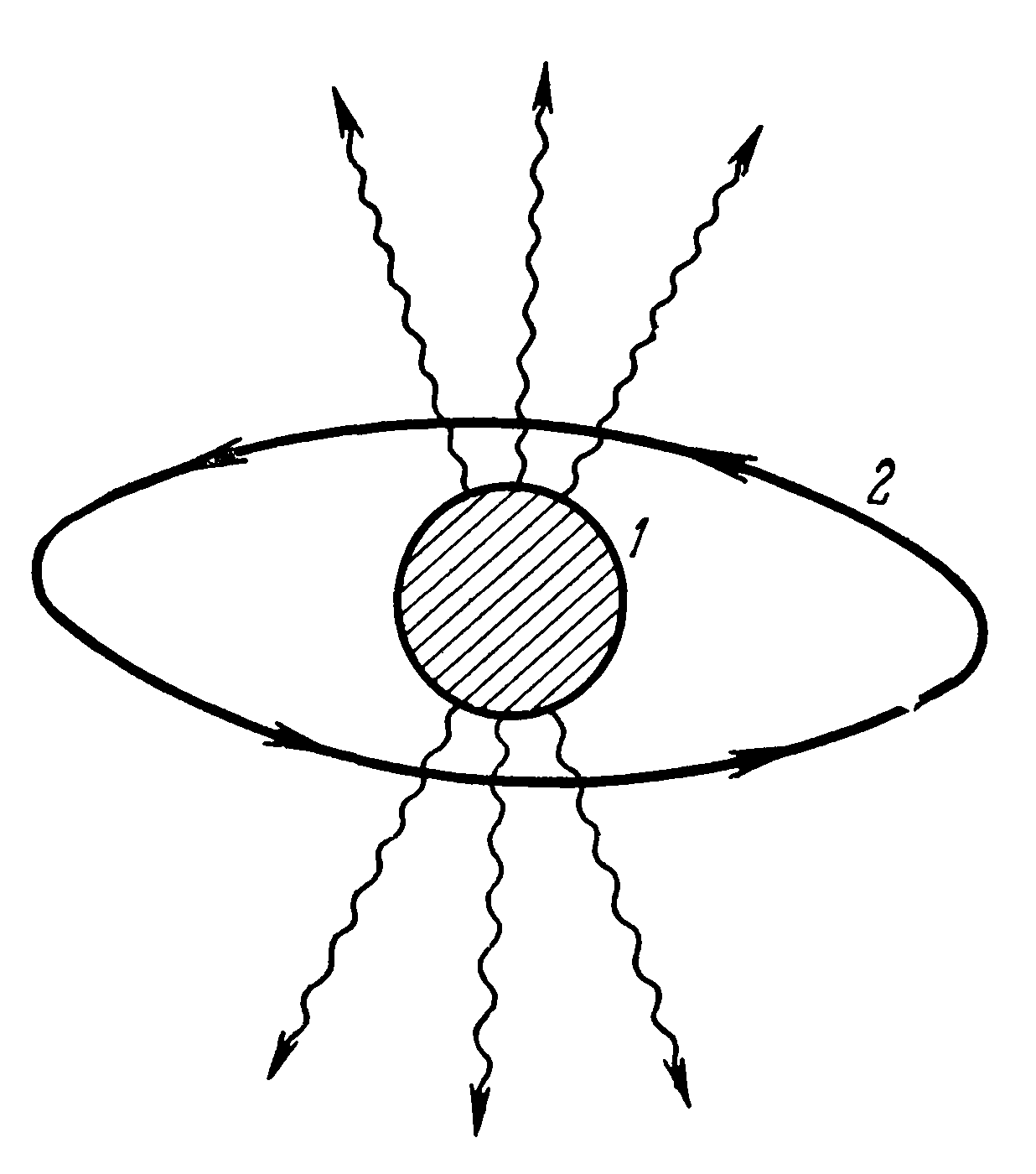 ействие закона сохранения четности можно продемонстрировать на эффекте Зеемана. Рассмотрим сферически симметричный источник света, например, нагретый шар 1 (рис. 2.23). В свободном состоянии излучение этого источника будет, изотропным, т. е. одинаковым во все стороны. Если же мы окружим этот источник круговым проводником 2, по которому течет ток, то излучение, скажем, в плоскости тока будет иным, чем излучение в направлении, перпендикулярном этой плоскости, за счет того, что созданное круговым током магнитное поле поляризует атомы и молекулы источника света. Закон сохранения четности здесь позволяет предсказать, что независимо от деталей углового распределения испускаемого света излучение будет зеркально симметричным относительно плоскости, в которой течет ток. Так, на рис. 2.23 излучение вверх будет точно таким же, как и излучение вниз.

Закон сохранения четности приводит к ряду ограничений (правил отбора), для различных реакций взаимопревращений ядер и элементарных частиц. В квантовой теории состояние системы n частиц описывается комплексной волновой функцией Ψ(r₁,…,r_n), зависящей от координат этих частиц.

Для протонов, нейтронов и электронов, т. е. для частиц, из которых состоят атомы и ядра, а также для ряда других микрочастиц определение четности эквивалентно разделению функций начетные и нечетные. Состояние системы n таких частиц называется четным, если ее волновая функция не меняется при изменении знаков координат всех частиц:

Ψ_четн(-r₁,…,-r_n)=Ψ_четн(r₁,…,r_n) (2.49)

и нечетным, если волновая функция при такой операции (называемой инверсией координат) меняет знак:

Ψ_нечетн(-r₁,…,-r_n)=-Ψ_нечетн(r₁,…,r_n) (2.50)

Связь этого определения четности с зеркальной симметрией обусловлена тем, что преобразование инверсии r→-r состоит из зеркального отражения относительно плоскости, проходящей через начало координат, с последующим поворотом на 180° вокруг оси, перпендикулярной этой плоскости. Для общего случая произвольных микрочастиц определения четности состояния (2.49), (2.50) приходится немного усложнить. Оказывается, что каждая частица с ненулевой массой покоя обладает неотъемлемой характеристикой, называемой внутренней четностью. Внутренняя четность П частицы является числом, равным либо +1, либо -1. Частицы, для которых П=+1, называются четными, а частицы с П=-1 называются нечетными. Охватывающее все частицы определение четности состояния таково: состояние четно, если

П₁,…,П_nΨ_четн(-r₁,…,-r_n)=Ψ_четн(r₁,…,r_n) (2.51)

и нечетно, если

П₁,…,П_nΨ_нечетн(-r₁,…,-r_n)=-Ψ_нечетн(r₁,…,r_n) (2.52)

В (2.51), (2.52) П₁,...,П_n- внутренние четности частиц.

Из этих формул могут бытьвыведены следующие простые правил:

а) Четность частицы с орбитальным моментом ℓ и внутренней четностью П равна

П (-1)^ℓ.

б) Внутренняя четность П₁₂ сложной системы, состоящей из двух частиц (и вообще из двух подсистем) с внутренними четностями П₁ и П₂ и с относительным орбитальным моментом ℓ, равна П₁П₂ (-1)^ℓ. При этом внутренней четностью системы частиц мы называем ее четность в состоянии с нулевым суммарным импульсом.

Из совокупности самых разных опытных данных следует, что внутренние четности протона, нейтрона и электрона можно положить равными единице. Тогда из правил а), б) следует важное для теории атомов и ядер соотношение: четность системы n нуклонов (или электронов) с орбитальными моментамиℓ₁,...,ℓ_n равна (-1)^{ℓ1+ ℓ2+…+ ℓn}. Только что изложенные правила определения четностей различных состояний неприменимы для фотонов (и вообще для частиц с нулевой массой покоя и ненулевым спином).

Основные состояния четно-четных ядер характеризуются положительной четностью. Основные состояния других ядер могут быть как четными, так и нечетными. Ядра в возбужденных состояниях могут иметь различную четность, не обязательно совпадающую с четностью основного состояния. Совокупность значений спина и четности называется характеристикой уровня ядра.