В этом документе содержатся ответы на следующие вопросы: 4,3,5,7,10,11,12,16,23,9,13,8,27,28,29,31,37,26,39,40,41,42,47,46,50,52 – идут именно в такой последовательности.

4.Радиус ядра

Первые представления о размерах атомного ядра были получены Резерфордом в результате опытов по изучению рассеяния α-частиц. Для согласования результатов опытов с расчетами потребовалось предположить, что значительная часть массы атома сосредоточена в его центральной части - ядре, которое можно представить в виде шара размером примерно 10^-12 см.

В дальнейшем размеры ядер определялись разными способами:

1. оценка радиуса α-радиоактивных ядер по постоянной α-распада; (см. § 17, п. 5);

2. анализ полуэмпирической формулы для массы и энергии связи ядра; (см. § 10);

3. исследование рентгеновского излучения µ-атомов; (см. § 106, п. 2);

4. изучение рассеяния быстрых нейтронов на ядрах;

5. измерение рассеяния быстрых электронов на ядрах.

Рассмотрим два последних способа.

1) Изучение рассеяния быстрых нейтронов на ядрах

Достаточно точно можно определить радиусы ядер при изучении взаимодействия быстрых нейтронов с атомными ядрами. Вероятность взаимодействия в ядерной физике харак­теризуется эффективным сечением σ, которое для быстрых дейтронов определяется следующим образом. Пусть N - поток нейтронов, падающих на 1 см² тонкой мишени (т. е. такой, что ядра мишени не перекрывают, не затеняют друг друга, рис. 27,а).Тогда эффективное сечение взаимодействия нейтрона с ядром определяется как σ = dN/(Nnδ) (4.1)

г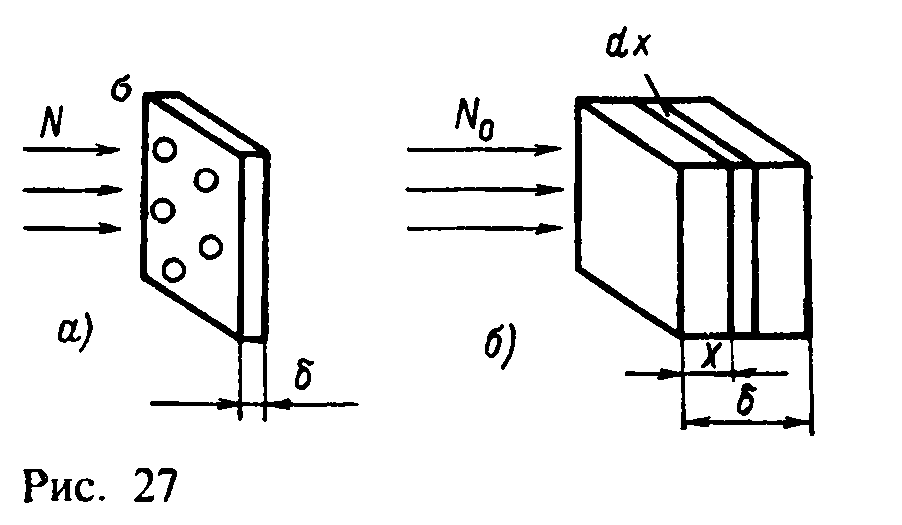 деdN - число взаимодейст­вий;n - концентрация ядер в мишени; δ -толщина мише­ни. Из выражения (4.1) следу­ет, что относительная доля dN/Nпровзаимодей-ствовавших нейтронов равна отно­сительной доли площади мишени dS=σnδ, занятой всемиядрами, если приписать σ наглядный физический смысл площади поперечного сечения ядра.

В случае толстой мишени плотность потока изменяется с глубинойx, и для оценки числа нейтронов, прошедших через мишень, очевидно, надо составить дифференциальное уравнение для некоторого тонкого слоя мишени dx на глубине х:

dN= - N(x)nσdx (4.2)

Здесь N(x) - число нейтронов, дошедших до слоя мишени на глубине х; dx - толщина слоя (рис. 27, б). Решение уравнения (4.2) получается в виде:

N(x) = N₀exp( - nσх)где N₀ - первичный поток нейтронов. (4.3)

Таким образом, для определения сечения взаимодействия быстрых нейтронов с ядрами достаточно измерить в специальном опыте ослабление интенсивности пучка нейтронов N(σ)/N₀ при прохождении его через мишень толщиной δ:

σ=-ln[N(δ)/N₀]/(Nδ) (4.4)

Чтобы получить радиус ядра, надо выразить σ через R.

На первый взгляд кажется, что эффективное сечение σ, имеющее физический смысл площади сечения ядра, должно быть равно πR². Это было бы действительно так, если бы взаимодействие быстрых (T_n=10 МэВ) нейтронов с ядрами ограничивалось рассмотренным выше неупругим рассеянием. Однако в действительности для быстрых нейтронов существует еще один процесс взаимодействия - упругое дифракционное рассеяние дебройлевской нейтронной волны на ядрах (подроб-нее см. § 44). Эффективное сечение этого процесса также равно πR². Таким образом, суммарное эффективное сечение взаимодействия быстрых нейтронов с ядрами: σ=2πR² (4.5)Поэтому из опытов по ослаблению пучка нейтронов можно получить сведения о радиусе атомных ядер мишени.

Были проведены опыты с нейтронами, имеющими энергию 14 и 25 МэВ. Они дали для радиуса ядер значениеR=r₀A^1/3,где r₀=1,4 10^-13 см.Аналогичный результат получен в опытах по изучению рассеяния нейтронов с энергией 90 МэВ (r₀=1,37 10^-13 см). Несколько меньшее значение (r₀=1,28 10^-13 см) найдено в опытах по изучению поглощения ядрами очень быстрых нейтронов (Т_n=1,4 ГэВ).

Таким образом, методы определения радиусов атомных ядер, основанные на изучении их взаимодействия с нейтронами, приводят к следующему результату:

R=r₀A^1/3, где r₀=(1,3÷1,4) 10^-13 см.