8.Потери напора в трубопроводе по длине и местные сопротивления.

Выше были получены два основных уравнения гидродинамики: уравнение сохранения энергии (уравнение Д. Бернулли), связывающее средние скорости и давления, и уравнение неразрывности потока (сохранения массы) для несжимаемой жидкости, которые были записаны в следующем виде:

;

.

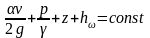При решении некоторых задач вполне достаточно этих уравнений, если пренебречь потерями энергии (напора) h_w, так как расход Q и полный напор H обычно заданы или могут быть определены.

Но большинство задач нельзя решить, если пренебречь потерями напора h_w. В таких случаях имеются два уравнения и три неизвестных v, р и h_w.

Для решения таких задач необходимо составить третье уравнение, связывающее между собой неизвестные величины. Наиболее подходящим, очевидно, будет уравнение, дающее зависимость h_w от скорости v.

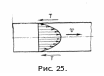
При движении потока между жидкостью и стенками, ограничивающими поток, возникают силы сопротивления. Кроме того, вследствие вязкости жидкости между ее отдельными слоями возникают силы сцепления, которые также затормаживают движение потока. Скорость движения частиц жидкости уменьшается по мере по мере удаления от оси потока к стенкам трубы, лотка и т. д. Равнодействующая сил сопротивления параллельна оси потока и направлена в сторону, противоположную направлению движения (рис. 25).

Для преодоления сил гидравлического трения и сохранения поступательного движения жидкости необходимо приложить силу, направленную в сторону движения и равную силам сопротивления. Работу этой силы называют потерями напора по длине потока (путевые потери напора) и обозначают через .

Сети трубопроводов, распределяющие или отводящие жидкость от потребителей, меняют свой диаметр (сечение); на сетях устраиваются повороты, ответвления, устанавливаются запорные устройства и т. п. В этих местах поток меняет спою форму, резко деформируется. Вследствие изменения формы возникают дополнительные силы сопротивления, так называемые местные сопротивления. На их преодоление расходуется напор. Напор, затрачиваемый на преодоление местных сопротивлений, называют местными потерями напора и обозначают через .

Общие потери напора равны сумме потерь напора по длине и местных

. (81)

Размерность потерь напора такая же, как и напора, т. е. метры столба жидкости.

9. Чем обусловлены потери напора в трубах по длине

Потери напора по длине, иначе их называют потерями напора на трение  , в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением  в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью

,

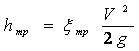где   - коэффициент сопротивления, обусловленный трением по длине.

При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине  и обратно пропорционален диаметру трубы

,

где l– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).

Из этого выражения нетрудно видеть, что значение l - коэффициент трения участка круглой трубы, длина которого равна её диаметру.

С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси

.