6.Модель идеального газа и его уравнения состояния

Идальный газ – это воображаемый газ, состоящий из упругих молекул, между которыми отсутствуют силы взаимного притяжения и отталкивания, а объем, занимаемы этими молекулами, бесконечно мал по сравнению с объемом пространства между ними.

Основные свойства ид. газа:

Объем частиц газа равен нулю

Импульс передается только при соударениях

Суммарная энергия частиц постоянна.

Термическим уравнением состояния идеального газа является уравнение Клапейрона –Менделеева PV=RT. Теплоемкостью вещества называется отношение бесконечно малого количества теплоты, подводимого к веществу в каком-либо процессе, к соответствующему бесконечно малому изменению его температуры. Таким образом, согласно молекулярно – кинетической теории теплоемкость идеального газа зависит только от сложности его молекулы (числа степеней свободы) и не зависит от температуры.

7.Термодинамическое уравнение состояния смеси идеальных газов, влажный воздух.

В термодинамике изучают газовые смеси, представляющие собой механическую смесь различных газов, между которыми отсутствуют химические реакции, т.е. газовые смеси не изменящие свои свойста. Каждый газ, входящий в состав смеси занимает весь объём и имеет температуру равную температуре смеси. Будем считать, что каждый газ подчиняется уравнению Клапейрона:

PiV=miRiT, то для газовой смеси массой m можна записать уравнение состояния в виде: pV=mRстT, где Rст=8314,2/µсм.

Давление смеси идеальных газов равно сумме парциальных давлений компонентов смеси (закон Дальтона):

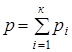
Смесь (раствор) - совокупность химически не взаимодействующих нескольких чистых веществ. Когда они образуют смесь, их называют компонентами, а саму смесь - многокомпонентной системой.

Примеры: воздух, водоаммиачные растворы, водка, сплавы металлов Частным случаем смесей (растворов) является газовая смесь (смесь различных газов) Пример: воздух, Смесь идеальных газов - совокупность материальных точек, отличающихся массой Ее можно рассматривать как идеальный газ с некоторыми средними характеристиками. Законы Дальтона — два физических закона, определяющих суммарное давление и растворимость смеси газов.

8.Калорическое уравнение состояния идеального газа. Уравнение Майера.

Калорическое уравнение идеального газа – уравнение, которое отражает зависимость внутренней энергии конкретной системы от термодинамических параметров можно получить опытным путём. Внутренняя энергия идеального газа зависит только от температуры. Это утверждение называют законом Джоуля.

U = νCvT.

Уравнение Майера - уравнение, устанавливающее связь между теплоёмкостями при постоянном давлении Cp и постоянном объёме Сv 1-го К.Моля идеального газа:

Cp-Cv=R, где R - газовая постоянная . Для произвольной массы (кг) вещества в состоянии идеального газа уравнение записывается в виде: Cp-Cv=(m/µ)R,

где µ - молекулярная масса газа. Уравнение Майера можно получить из общего соотношения

,если учесть что для идеального газа справедливо уравнению Клапейрона.