Глава 4 Расчет закрытой цилиндрической зубчатой передачи
Расчет зубчатой закрытой передачи производится в два этапа: первый расчет – проектный, второй – проверочный. Проектный выполняется по допускаемым контактным напряжениям с целью определения геометрических параметров редукторной пары. В процессе проектного расчета задаются целым рядом табличных величин и коэффициентов; результаты некоторых расчетных величин округляют до целых или стандартных значений; в поиске оптимальных решений приходится неоднократно делать пересчеты. Поэтому после окончательного определения параметров зацепления выполняют проверочный расчет. Он должен подтвердить правильность выбора табличных величин, коэффициентов и полученных результатов в проектном расчете, а также определить соотношения между расчетными и допускаемыми напряжениями изгибной и контактной выносливости. При неудовлетворительных результатах проверочного расчета нужно изменить параметры передачи и повторить проверку (рисунок 4.1).
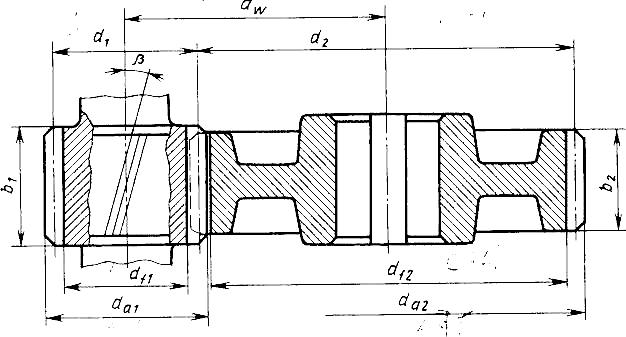
Рисунок 4.1 Геометрические параметры цилиндрической зубчатой передачи
4.1 Проектный расчет
4.1 Определяем главный параметр – межосевое расстояние аw, мм:
(4.1)
где Ка = 43 – вспомогательный коэффициент;
= 0,3 – коэффициент ширины венца колеса;
Т2 = 272,23 Н∙м вращающий момент на тихоходном валу;
=514,3 Н/мм2
– допустимое контактное напряжение
колеса с менее прочным зубом (см. табл.
3.1);
КНβ = 1. коэффициент неравномерности нагрузки по длине зуба;
и = 5 передаточное число редуктора.
Подставив данные, находим:
мм.
Полученное значение межосевого расстояния аw =133,08 мм, округляем до ближайшего значения из ряда нормальных линейных размеров аw = 135мм [7, табл. 13.15, стр. 326].
4.2 Определяем модуль зацепления т, мм:
, (4.2)
где Кт = 5,8 – вспомогательный коэффициент;
мм
– делительный диаметр колеса;
мм
– ширина венца колеса;
=192 Н/мм2 – допустимое напряжение изгиба
колеса с менее прочным зубом (см. табл.
3.1);
Подставив данные, находим:
мм.
Полученное значение модуля т = 1,81 мм, округляем в большую сторону до стандартного значения из ряда чисел т = 2 мм [7, стр. 62].
4.3 Определяем угол наклона зубьев βmin для косозубой передачи:
. (4.3)
4.4 Определяем суммарное число зубьев шестерни и колеса:
(4.5)
где т = 2 мм – модуль зацепления;
аw =135 мм – межосевое расстояние;
βmin = 9,953о – угол наклона зубьев.
Подставив данные, находим:
зуба.
4.5 Уточняем действительную величину угла наклона зубьев:
. (4.5)
4.6 Определяем число зубьев шестерни:
зуба. (4.6)
4.7 Определяем число зубьев колеса:
зубьев. (4.7)
4.8 Определяем фактическое передаточное число иф и проверяем его отклонение от заданного и:
; (4.8)
. (4.9)
Подставив данные, находим:
- условие выполняется.
4.9 Определяем фактическое межосевое расстояние:
мм. (4.10)
4.10 Определяем основные геометрические параметры передачи, мм:
а) Диаметр делительный:
шестерни:
мм; (4.11)
колеса:
мм; (4.12)
б) Диаметр вершин зубьев:
шестерни:
мм; (4.13)
колеса:
мм; (4.14)
в) Диаметр впадин зубьев:
шестерни:
мм; (4.13)
колеса:
мм; (4.14)
г) Ширина венца:
колеса: мм; (4.15)
шестерни:
мм. (4.16)
Значение ширины
зубчатых венцов округляем до целого
числа из ряда нормальных линейных
размеров [7, табл. 13.15, стр. 326]:
мм,
мм.