2.3. Применение метода смещения узлов для измерения параметров нерегулярностей волноводного тракта.

Рассмотренный выше метод Татаринова при измерении параметров реактивных нерегулярностей в тракте имеет тот недостаток, что вследствие неидеального согласования «согласованной нагрузки» в изменения вносится систематическая погрешность (см. задачу ПР2.3). Кроме того, имеет место так же погрешность измерения КБВ с помощью измерительной линии, связанная с неквадратичностью характеристики детектора, возникающей при повышенном уровне сигнала в тракте.

Метод смещения узлов свободен от этих недостатков. Однако в отличие от метода Татаринова данный метод применим для измерения характеристик только реактивных нерегулярностей тракта.

При проведении измерений методом смещения узлов на выход проходной секции волновода с исследуемой реактивной нерегулярностью, подключается короткозамкнутый волноводный шлейф регулируемой длины. Поскольку получившаяся нагрузка не имеет потерь, в тракте устанавливается режим стоячей волны. Изменяя длину шлейфа и наблюдая за смещением узла напряжения в измерительной линии, можно определить проводимость нерегулярности, включенной в тракт между выходом измерительной линии и шлейфом.

Поясним данную методику более подробно.

Пусть выход измерительной линии (сечение 1 на рис. 1.7) нагружен на короткозамкнутый отрезок волновода (короткозамкнутый шлейф) длиной 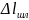. Если =0, то распределение напряжения вдоль линии (сплошная линия на рис. 1.7) от сечения короткого замыкания в направлении к генератору будет определяться законом Sin(βl), где отсчитывается от сечения 1 в сторону генератора.

Установим длину шлейфа равной . При этом распределение напряжения в линии будет описываться тем же законом, но вся картина стоячих волн сдвинется в сторону нагрузки на расстояние .

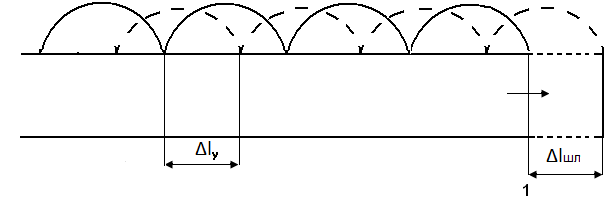
Рис. ПР2.2 Распределение напряжения вдоль линии, нагруженной на реактивную нагрузку.

Если теперь шлейф в сечении 1 заменить реактивной нагрузкой с проводимостью, равной проводимости шлейфа y_ш=-jctg(βΔl_шл)_, то распределение напряжения в линии останется точно таким же, как и при подключенном шлейфе, при этом сдвиг узла напряжения в линии останется равным Δl_у.

Отсюда следует, что если к линии в сечении 1 подсоединить вместо шлейфа неизвестную реактивную нагрузку и измерить сдвиг узла Δl_у относительно положения узлов при режиме кз в сечении 1, то неизвестную реактивную проводимость нагрузки можно рассчитать по формуле y_н=-jctg(βΔl_у).

Учитывая сказанное выше для измерения проводимости нерегулярности в волноводном тракте может быть использована следующая процедура:

Шаг 1. Подсоединяем к выходу измерительной линии в сечении 1 (рис.1.8) короткозамкнутую секцию волновода такой длины 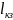, чтобы её сечение короткого замыкания приходилось бы точно на сечение, в котором будет располагаться измеряемая нерегулярность после ее подключения в составе проходной секции. Измеряя распределение напряжения вдоль измерительной линии (сплошная кривая на рис. 1.8), находим положение узлов в распределении напряжения.

Шаг 2. Подключаем на выход измерительной линии проходную волноводную секцию длиной l_секц с измеряемой нерегулярностью, нагруженную в свою очередь на короткозамкнутый шлейф изменяемой длины. Подбираем длину шлейфа такой, чтобы положение узлов в измерительной линии совпадало с их положением, зафиксированным при подключенной короткозамкнутой секции. Это означает, что поршень короткозамыкателя оказался на расстоянии от нерегулярности, равном целому числу полуволн nλ_в/2 (на рис n=1), в результате чего сечение узла напряжения совпало с сечением, в котором находится нерегулярность, обеспечив в этом сечении режим кз. При этом эквивалентная проводимость в сечении включения нерегулярности оказывается равной бесконечности, и проводимость самой нерегулярности никак не влияет на положение узлов в линии.

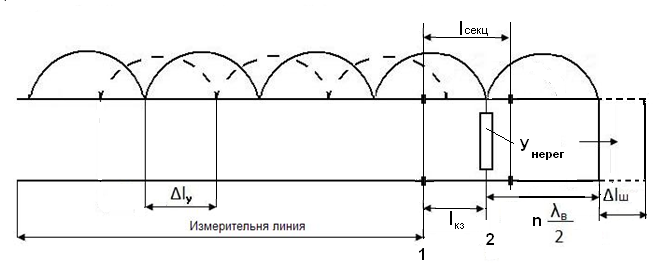
Рис. ПР2.3 Пояснение к методу смещения узлов.

Шаг 3. Увеличим длину шлейфа на Δl_шл. При этом в измерительной линии получаем новое распределение напряжения (нанесено пунктиром), узлы которого смещены на расстояние Δl_у относительно узлов на шаге 2. Если бы в сечении 2 нерегулярность отсутствовала, то Δl_у и Δl_шл были бы одинаковы. Если же в это сечение включена некая реактивность, то ее проводимость y_н суммируется с проводимостью шлейфа. При этом сдвиг узла будет таким, как если бы мы подключили в сечение 2 вместо нерегулярности и реального шлейфа эквивалентный шлейф длино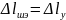й . Таким образом проводимость эквивалентного шлейфа оказывается равной сумме проводимости реального шлейфа и проводимости нерегулярности:

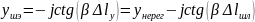
откуда:

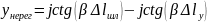(ПР2.3)