ЭУМК

Техническая Электродинамика

Практическое занятие 2

2.1. Метод в.В.Татаринова измерения входных сопротивлений (проводимостей) нагрузок на свч. Теоретическое введение

Наиболее универсальным методом измерения сопротивлений (проводимостей) нагрузок на СВЧ является метод Татаринова. В основе метода лежат соотношения, связывающие эквивалентные нормированные сопротивления (проводимости) в двух сечениях и 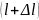линии передачи:

. (ПР2.1)

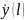Где и нормированные сопротивления в сечении линии, 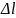положительно, если сечение расположено ближе к генератору по сравнению с сечением и отрицательно в противоположном случае.

Идея метода Татаринова состоит в том, что в линии, нагруженной на измеряемую нагрузку, сначала находится сечение, в котором эквивалентное сопротивление (проводимость) известны, далее измеряется расстояние от этого сечения до сечения, принимаемого за сечение входа нагрузки, и с помощью соотношений (ПР2.1) или круговой номограммы находится искомое сопротивление нагрузки.

Сечениями линии, в которых сопротивление или проводимость легко определить, являются сечения узла или пучности в продольном распределении напряжения.

В сечении узла полное напряжение минимально, а ток максимален.

Выражение для расчета сопротивления в сечении узла напряжения, выглядит следующими образом

.

Сравнивая полученное выражение с полученным в лекции выражением для расчета КБВ, приходим к выводу, что в сечении узла напряжения эквивалентное сопротивление чисто активное и равно значению КБВ, создаваемому в линии измеряемой нагрузкой (проводимость равна КСВ).

Таким образом, если в формуле (ПР2.1) принять, что есть расстояние от сечения узла напряжения до сечения входа нагрузки (со знаком минус), а сопротивление равно КБВ (проводимость =КСВ), то будет искомым сопротивлением, а 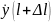соответственно проводимостью нагрузки в сечении ее входа:

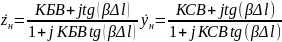. (ПР2.2)

Поскольку расстояние , как правило, сложно измерить, находят некоторое сечение в пределах шкалы измерительной линии, в котором эквивалентное сопротивление равно измеряемому сопротивлению нагрузки и определяют сопротивление в этом сечении.

В качестве такого сечения может быть взято любое сечение, отстоящее от сечения входа нагрузки на расстоянии, равном целому числу полуволн, (сопротивление (проводимость) меняется вдоль линии по периодическому закону с периодом λ_в/2).

Для определения положения искомых сечений обеспечивают в сечении линии, соответствующем сечению входа нагрузки, режим короткого замыкания. Любой узел в полученном продольном распределении напряжения (назовем его узлом кз) оказывается отстоящим от сечения входа нагрузки на расстоянии, кратном λ_в/2, и положение какого-либо из этих узлов в пределах шкалы измерительной линии может быть использовано для определения сопротивления нагрузки.

При расчете сопротивлений (проводимостей) вместо соотношений (ПР2.2) может быть использована круговая номограмма.

Измерение параметров нерегулярностей волноводного тракта.

Под нерегулярностями волноводного тракта мы далее будем понимать сосредоточенные нерегулярности внутри тракта со схемой замещения в виде параллельно включаемой в линию реактивности (диафрагмы, штыри).

При измерении в лаборатории характеристик подобных нерегулярностей проходная секция волновода, в которой располагается нерегулярность, подключается к измерительной линии, а к ее свободному концу подключается нагрузка, проводимость которой известна и может быть пересчитана в проводимость y_нагр в сечении включения нерегулярности. Далее в сечении нерегулярности измеряется суммарная комплексная проводимость y_Σ, состоящая из проводимости нерегулярности и y_нагр, на основании чего определяется проводимость нерегулярности.