1.3. Нормированные сопротивления и проводимости.

Отношение полного нормированного напряжения к полному нормированному току в сечении эквивалентной длинной линии представляет собой эквивалентное полное нормированное сопротивление (безразмерное) в сечении линии:

, (1.10)

Обратная величина является полной нормированной проводимостью (так же безразмерной):

(1.11)

Эквивалентное полное нормированное сопротивление имеет тот физический смысл, что оно по существу является входным сопротивлением отрезка линии длиной от сечения до сечения входа нагрузки с подключенной на конце нагрузкой.

Будем считать далее, что затухание в линии отсутствует.

Подставляя в (1.10), (1.11) величину в форме (1.5) и учитывая, что:

после несложных преобразований, приходим к выражениям, позволяющим найти сопротивление (проводимость) в сечении , зная его в сечении :

. (1.12)

При использовании соотношений (1.12) необходимо помнить, что положительно при сдвиге от сечения в сторону к генератору и отрицательно при сдвиге в сторону нагрузки.

Если под понимать сопротивление нагрузки включенной в линию в сечении =0, то из (1.12) можно получить выражения, позволяющие пересчитать сопротивление (проводимость) нагрузки в любое сечение линии передачи, отстоящее на расстояние l в сторону генератора от сечения входа нагрузки

(1.13)

при этом положительно и представляет собой расстояние от сечения входа нагрузки до сечения линии, в котором мы хотим определить эквивалентное сопротивление.

в сечении =0 связаны соотношениями

(1.14)

Для линий, в которых волновое сопротивление может быть определено однозначно, можно перейти от нормированных величин сопротивлений и проводимостей к ненормированным величинам (обозначаются заглавными буквами и ) используя условия нормировки ,

. (1.15)

При этом размерность сопротивления в (1.15) - ом, а проводимости - 1/ом.

Поскольку используемые для трансформации отрезки линий передачи могут отличаться от основной линии передачи в тракте, по размерам поперечного сечения, по конструктивному выполнению, по применяемому типу волн, в схемах замещения это может учитываеться введением неединичных безразмерных волновых сопротивлений z_в.

Для этого в (1.15) все величины сопротивлений поделим на z_во, а все проводимости умножим на z_во, где z_во - волновое сопротивление основной линии.

При этом мы получаем соотношения для пересчета сопротивлений и проводимостей, нормированных к волновому сопротивлению z_во основной линии, через отрезок линии длиной с измененным волновым сопротивлением z_в, так же нормированным к величине z_во:

. (1.16)

В (1.16) все сопротивления и проводимости являются безразмерными.

Круговая номограмма полных сопротивлений (проводимостей).

В инженерной практике, когда точность определения длин отрезков линий, входящих в проектируемое устройство, не превышает двух значащих цифр, для пересчета сопротивлений (проводимостей) из одного сечения линии передачи в другое, удобно использовать круговую номограмму (диаграмму) полных сопротивлений (проводимостей), называемую также номограммой Вольперта или номограммой Вольперта – Смита. В дальнейшем изложении везде будет использоваться термин «круговая номограмма». Стандартный вид диаграммы представлен в Приложении 1.

Идея построения круговой номограммы достаточно проста. Представим на комплексной плоскости (рис. 1.1) коэффициент отражения в векторной форме.

Комплексная величина изображается точкой на комплексной плоскости с радиусом вектором равным . Изменение при движении по линии от некоторого сечения , на расстояние Δ описывается в линии без потерь соотношением

При этом, поскольку потерь в линии нет, модуль постоянен по длине линии.

Фаза коэффициента отражения характеризуется углом , отсчитываемым между положительной действительной осью и направлением вектора . При перемещении к генератору приращение фазы Δφ отрицательно (Δ >0), а при движении к нагрузке – положительно (Δ <0). Фаза коэффициента отражения меняется на 360^о при смещении вдоль линии на расстояние, равное половине длины волны. Направление движения на номограмме обычно указывается стрелками с маркировкой «к нагрузке» и «к генератору».

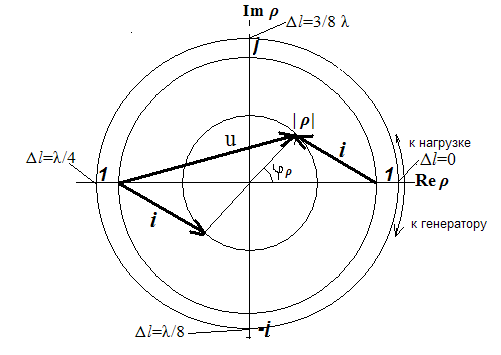
Рис. 1.1 Комплексная плоскость коэффициента отражения

На внешней окружности номограммы c радиусом несколько большим, чем наносится равномерная шкала расстояний, на которой отмечаются значения Δ в пределах от 0 до λ_в/2 (как указано выше, периодическая функция с периодом λ_в/2) и соответствующее величине Δ значение фазы (4πΔ /λ_в) в пределах от 0 до 360 град. При этом, поскольку для пересчета из одного сечения линии в другое необходимо знать только разностную величину Δ , начало отсчета шкалы расстояний может располагаться в любой точке на проградуированной окружности. Стандартно его располагают на действительной оси.

Если теперь на рассматриваемую номограмму в каждой точке нанести величины реальной и мнимой составляющих нормированного сопротивления или проводимости, найденные с использованием соотношений

,

и соединить одинаковые значения непрерывной линией, то получится картина, изображенная на рис.1.2, а и б.

На этих рисунках линии постоянной активной составляющей Re z и Re y изображаются окружностями с центром на горизонтальной оси, имеющими одну общую точку касания (т.2). Внешняя окружность, проходящая через т.1 и т.2, соответствует на представленных номограммах значениям Rez=0 (Rey=0); окружность, проходящая через начало координат соответствует значениям Rez=1 (Rey=1); на горизонтальной оси при движении от т.1 к т.2. Rez и (Rey) меняются от 0 (т.1) до бесконечности (т.2.).

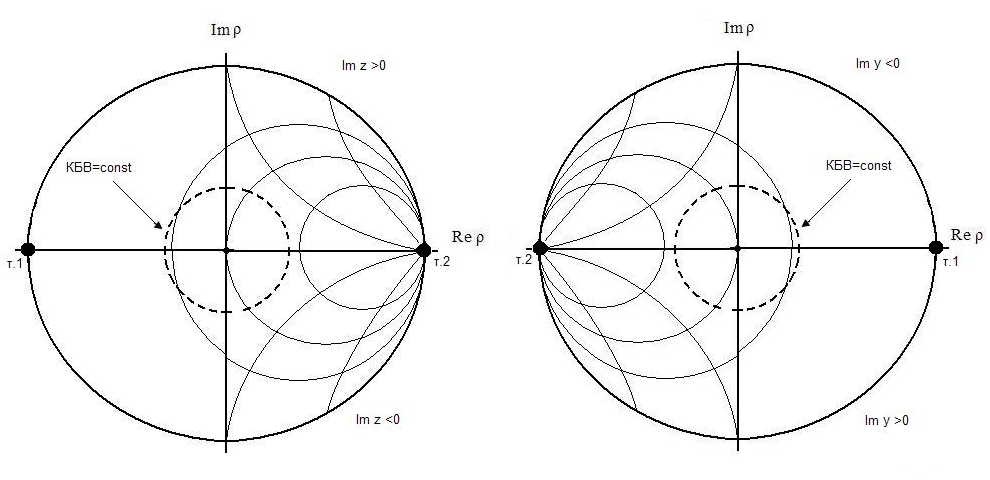
а) б)

Рис. 1.2. а - номограмма сопротивлений; б - номограмма проводимостей

Линии постоянной реактивной составляющей так же являются частями окружностей с центром на вертикальной оси, проходящей через т.2. Знак реактивности выше и ниже действительной оси указан на рис.1.2.

Концентрические окружности с центром в начале координат (одна из которых изображена на номограмме пунктиром) соответствуют линиям постоянного значения модуля коэффициента отражения, но для удобства использования они маркируются величиной КБВ

Если представленную на рис.1.2 номограмму сопротивлений повернуть на 90˚ по часовой стрелке, а номограмму проводимостей против часовой стрелки, получится одна и та же по виду номограмма (см. приложение 1). Все маркировки для обеих номограмм полностью совпадают. Поэтому номограмму в повернутом виде можно считать номограммой сопротивлений, если с её помощью предполагается осуществлять пересчет сопротивлений, либо номограммой проводимостей, если будут пересчитываться проводимости.

Основная задача, которую позволяет решить круговая номограмма это пересчет эквивалентных комплексных сопротивлений (проводимостей) из одного сечения линии в другое, не прибегая к прямому использованию соответствующих формул.

Следует отметить, что пересчет сопротивлений (проводимостей) по номограмме может осуществляться только для нормированных величин сопротивлений и проводимостей.

Использование круговой номограммы для построения распределения нормированных напряжения и тока вдоль линии с нагрузкой.

Учитывая, что исходным для построения круговой номограммы является комплексная плоскость коэффициента отражения (рис. 1.2), можно использовать рассматриваемую диаграмму для нахождения изменения напряжения и тока вдоль линии, нагруженной на некоторую нагрузку.

На лекции было показано, что нормированные напряжение и ток определяются из соотношений

(1.1)

На комплексной плоскости коэффициента отражения на рис. 1.1 показаны векторные диаграммы, соответствующие напряжению и току. Начало единичного вектора, берется в точке, соответствующей на комплексной плоскости значению -1.

Задачи, решаемые на практическом занятии

Рассмотрим несколько примеров использования круговой номограммы.

Задача ПР1.1.

Пересчитать комплексное нормированное сопротивление из сечения в сечение в сторону генератора. ( =0,065).

Процедура пересчета включает следующие шаги:

Шаг 1. Находим на круговой номограмме сопротивлений точку, соответствующую сопротивлению в сечении . Она лежит на пересечении окружности постоянного активного сопротивления, равного Re и линии постоянного реактивного сопротивления, равного Im (т.1 на рис.1.3)

Определяем круг КБВ которому соответствует значение (КБВ=0,3). Переходим из т.1 по линии постоянного КБВ на расстояние =0,065 в сторону генератора. Для этого проводим через точку 1 радиус вектор (прямая, проходящая через центр номограммы и заданную точку) Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает нам возможность зафиксировать условное положение сечения на этой шкале (т.2 ).

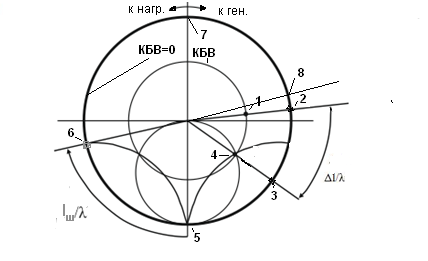
Рис. 1.3 Использование круговой номограммы для пересчета сопротивлений и проводимостей

Шаг 2. Отсчитываем от точки 2 по шкале расстояний величину в требуемом направлении (по поставленному в рассматриваемой задаче условию в сторону к генератору). Отмечаем на шкале расстояний полученную точку (т.3, и проводим через нее радиус вектор.

Шаг 3. Находим пересечение радиус вектора и круга КБВ=0,3. Значение сопротивления в точке пересечения (т.4) и есть искомое значение сопротивления в сечении

ОТВЕТ:

Задача ПР1.2.

Одной из задач, часто возникающих при проведении измерений и расчетов, является задача нахождения комплексного значения проводимости по известной величине сопротивления и наоборот. Данное преобразование может быть легко проведено с помощью круговой номограммы.

Пусть в некотором сечении линии нам известно значение нормированного сопротивления . Используя формулы для пересчета сопротивлений (проводимостей) из одного сечения линии в другое легко получить что:

т.е. при пересчете нормированного сопротивления из сечения в сечение, отстоящее от него на расстояние 0,25λ в сторону генератора или нагрузки, мы получаем значение сопротивления, численно равное значению проводимости в исходном сечении .

На круговой номограмме сопротивлений (рис. 4) описанная процедура пересчета сводится к нахождению сопротивления в точке т. 2, расположенной на номограмме сопротивлений диаметрально противоположно исходной точке (т.1), в которой сопротивление известно.

Аналогично с использованием номограммы проводимости находится сопротивление в заданном сечении линии по известной проводимости.

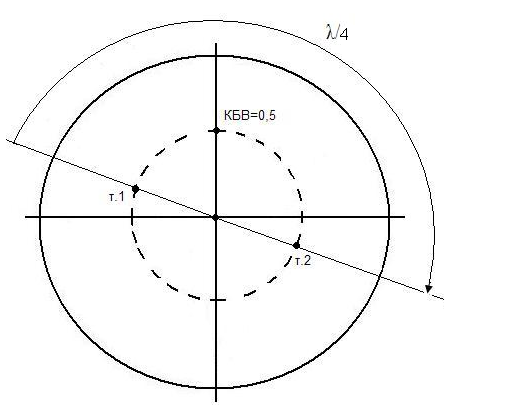
Рис. 1.4 Определение проводимости по известному сопротивлению с помощью круговой номограммы

Задача ПР1.3.

Определить нормированное сопротивление и проводимость на входе шлейфа с холостым ходом в сечении нагрузки при его длине .

Шаг 1. Находим в рассматриваемом отрезке линии (шлейфе) сечение, в котором сопротивление известно. Для нашего случая - это сечение нагрузки, сопротивление которой равно бесконечности (режим хх на конце шлейфа). На номограмме сопротивлений рис. 3 сопротивление равно бесконечности в т.5, принадлежащей кругу КБВ=0.

Проводим радиус вектор через точку 5. Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает условное положение сечения /λ на этой шкале (0.25).

Шаг 2. Отсчитываем от найденной точки на шкале расстояний величину в направлении к генератору. Отмечаем на шкале расстояний полученную точку (т.6) и проводим через нее радиус вектор.

Шаг 3. Находим пересечение радиус вектора и круга КБВ=0. Значение сопротивления в точке пересечения z_ш=-j1,43 и есть искомое значение реактивного сопротивления на входе шлейфа (активная составляющая сопротивления на круге КБВ=0 равна нулю, поскольку этот круг одновременно является кругом, на котором Rez=0).

ОТВЕТ: z_ш=-j1,43

Проводимость может быть найдена путем пересчета сопротивления в проводимость по методике, изложенной в предыдущем примере (y_ш = j0,69).

Задача ПР1.4.

Определить длину шлейфа с холостым ходом в сечении нагрузки, имеющего на входе заданную нормированную проводимость y_ш = j0,65.

Будем считать, что изображенная на рис. 3 номограмма есть номограмма проводимостей (выше отмечалось, что номограммы сопротивлений и проводимостей внешне не отличаются).

Шаг 1. В сечении нагрузки на конце шлейфа, проводимость равна нулю (режим хх). На номограмме проводимостей на рис. 3 проводимость равная 0 соответствует точке 7, принадлежащей кругу КБВ=0.

Проводим радиус вектор через точку 7. Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает условное положение сечения /λ на этой шкале (0).

Шаг 2. Двигаясь от точки 7 по кругу КБВ=0 в сторону генератора, доходим до т.8, в которой проводимость равна заданной. Проводим через т.8 радиус-вектор и отмечаем на шкале расстояний соответствующее т.8 значение.

Расстояние от точки 7 до точки 8 и есть искомая длина шлейфа.

ОТВЕТ: =0,095.

Задача ПР1.5.

Определить нормированную проводимость на входе шлейфа длиной с коротким замыканием в сечении нагрузки.

Шаг 1. Сечение, в котором проводимость известна является сечением нагрузки, проводимость которой в данном случае равна бесконечности (режим кз на конце шлейфа). На номограмме рис. 3 (номограмму на рис 3 мы рассматриваем как номограмму проводимостей) проводимость равна бесконечности в т.5, принадлежащей кругу КБВ=0.

Проводим радиус вектор через точку 5. Пересечение этого радиус-вектора с окружностью, на которой нанесена шкала расстояний, дает условное положение сечения /λ на этой шкале (0.25).

Шаг 2. Отсчитываем от найденной точки на шкале расстояний величину = 0,096 в направлении к генератору. Отмечаем на шкале расстояний полученную точку (т.6) и проводим через нее радиус вектор.

Шаг 3. Находим пересечение построенного радиус вектора и круга КБВ=0. Значение проводимости в точке пересечения y_ш=-j1,43 и есть искомое значение реактивной проводимости на входе короткозамкнутого шлейфа (активная составляющая проводимости на круге КБВ=0 равна нулю).

ОТВЕТ: y_ш=-j1,43

Задание на дом

1. С помощью круговой номограммы пересчитать сопротивление z = 0,5 - j1,5 в проводимость.

2. Для сопротивления нагрузки, равного z_н=2,5+j1,0, построить распределение нормированных напряжения и тока вдоль линии питания при движении от нагрузки в сторону к генератору в пределах одной длины волны.

3. Линия передачи с волновым сопротивлением z_в=75 Ом нагружена на сопротивление z_н =30+j45 Ом. Определить модуль коэффициента отражения от нагрузки. Какой КСВ установится в линии?

4. В линии передачи установился режим стоячей волны с КСВ=1,5. Чему равен модуль коэффициента отражения?

5. Нарисуйте графики изменения активной и реактивной составляющих эквивалентного сопротивления в сечении линии передачи при движении от нагрузки z_н=0,6+j0,3 в сторону генератора в пределах одной длины волны.

Приложение 1