6

ЭУМК

Техническая Электродинамика

Лекция 3

3.1 Нормированные напряжения и токи.

Электродинамическое описание электромагнитного поля в линии передачи с помощью векторных функций Е и Н содержит в себе существенно больше информации, чем может потребоваться при расчете и проектировании трактов СВЧ. Поэтому подробности структуры полей, распределения и направления векторов поля, величина волнового сопротивления, измеренная в омах, после того, как выбран конкретный тип линии передачи, имеют второстепенное значение и при проектировании тракта эти факторы желательно из рассмотрения исключить.

Достигается это построением универсальной математической модели в виде эквивалентной длинной линии. В эквивалентной длинной линии векторные функции распределения полей в поперечных сечениях заменяются интегральными (усредненными) мерами электромагнитного поля - эквивалентными нормированными напряжениями и токами для падающей и отраженной волн.

Напряжения 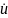и токи падающей и отраженной волн в нормированном виде для сечения линии передачи вводятся с помощью соотношений:

,

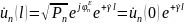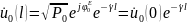, (3.1)

,

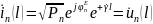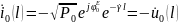
где как указывалось выше координата , направленная вдоль линии, отсчитывается от некоторого произвольного сечения линии, в котором полагается равным 0. Чаще всего сечение 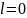совмещается с сечением входа нагрузки.

Модули нормированных напряжений и токов падающей и отраженной волн в (3.1) - представляют собой квадратные корни из соответствующих мощностей и поэтому имеют одинаковую размерность 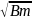. Фазы нормированных напряжений падающей и отраженной волн принимаются равными фазам поперечных компонентов поля Е для соответствующих волн.

При отсутствии в линии омических потерь амплитуды напряжения обеих волн (падающей и отраженной) неизменны в любом сечении тракта и все минимумы и максимумы в продольном распределении напряжения в линии одинаковы. КБВ также постоянен по длине линии.

Исходя из сказанного выше для распространяющейся волны любого типа в линии передачи могут быть формально введены следующие параметры:

1) полное нормированное напряжение в сечении (размерность ) в виде суммы нормированных напряжений падающей и отраженной волн:

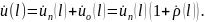(3.2)

2) полный нормированный ток (размерность ) в виде разности нормированных напряжений падающей и отраженной волн:

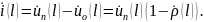(3.3)

Мощность, переносимая в линии бегущей волной, может быть вычислена через нормированные токи и напряжения как:

*)

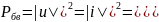где 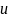и действующие значения напряжения и тока.

3.2. Нормированные сопротивления и проводимости.

Отношение полного нормированного напряжения к полному нормированному току в сечении эквивалентной длинной линии представляет собой эквивалентное полное нормированное сопротивление (безразмерное) в сечении линии:

(3.4)

Обратная величина является полной нормированной проводимостью (так же безразмерной):

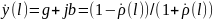(3.5)

В отличие от приведенных ранее выражений в (3.4) и (3.5) отсутствует волновое сопротивление, поскольку в соответствии с данным выше определением (3.1) оно оказывается равным единице.

Будем считать далее, что затухание в линии отсутствует.

Из сравнения выражений для нормированных и ненормированных сопротивлений и проводимостей следует что

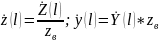(3.6)

Используя эти выражения, приходим к формулам для пересчета нормированных

сопротивлений (проводимостей) в сечение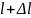 из сечения :

. (3.7)

При использовании соотношений (3.7) необходимо помнить, что 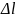положительно при сдвиге от сечения в сторону к генератору и отрицательно при сдвиге в сторону нагрузки.

Если под 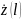понимать сопротивление нагрузки 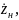включенной в линию в сечении =0, то из (3.7) можно получить выражения, позволяющие пересчитать сопротивление (проводимость) нагрузки в любое сечение линии передачи, отстоящее на расстояние 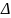l в сторону генератора от сечения входа нагрузки

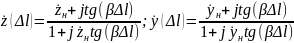(3.8)

при этом 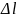положительно и представляет собой расстояние от сечения входа нагрузки до сечения линии, в котором мы хотим определить эквивалентное сопротивление.

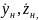
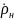в сечении =0 связаны соотношениями

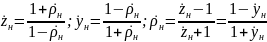(3.9)

Поскольку используемые для трансформации отрезки линий передачи могут отличаться от основной линии передачи в тракте, по размерам поперечного сечения, по конструктивному выполнению, по применяемому типу волн, в схемах замещения это может учитываться введением неединичных безразмерных волновых сопротивлений z_в.

Для этого в (2.14), (2.15) (предыдущая лекция) все величины сопротивлений поделим на z_во, а все проводимости умножим на z_во, где z_во - волновое сопротивление основной линии.

При этом мы получаем соотношения для пересчета сопротивлений и проводимостей, нормированных к волновому сопротивлению z_во основной линии, через отрезок линии длиной с измененным волновым сопротивлением z_вн, так же нормированным к величине z_во:

. (3.10)

В (3.10) все сопротивления и проводимости являются безразмерными.

В инженерной практике, когда точность определения длин отрезков линий, входящих в проектируемое устройство, не превышает двух значащих цифр, для пересчета сопротивлений (проводимостей) из одного сечения линии передачи в другое, удобно использовать круговую номограмму (диаграмму) полных сопротивлений (проводимостей), называемую также номограммой Вольперта или номограммой Вольперта – Смита.

Принцип построения номограммы и примеры ее использования рассматриваются на упражнениях.