1. Прямой, обратный, дополнительный коды. Примеры выполнения операции сложения.

Дополнительный код

Преобразование числа из прямого кода в дополнительный код осуществляется по следующему алгоритму.

Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;

Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Обратный код

Пример. Двоичное представление числа 5 есть 101, его 10-разрядное двоичное представление — 0000000101. Обратный 10-разрядный двоичный код числа −5 есть 1111111010.

2. Накапливающий сумматор.

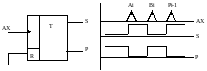
Накапливающий сумматор позволяет сохранить результат сложения по фронту сигнала, P вырабатывает сигнал переноса в старший разряд

3. Комбинационный сумматор.

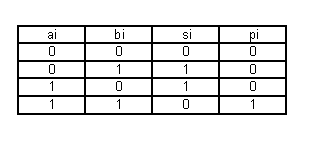
4. Параллельный двоичный сумматор (на основе накапливающих).

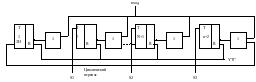
t_сум=t_mp+(n+2)*t_mp+t_mp=(n+4)* t_mp=n*t_mp

Где t_mp время ожидания, даже если сумма уже произошла

S1-S3 – выходы суммы

ЗН- знак числа

Перед каждой новой суммой на выход Y”0” поступает сигнал, которые сбрасывает триггеры в 0.

Циклический перенос используется при обратном коде (число инвертируется, после суммируется, если был перенос, то 1 переходит в старший разряд)

Недостаток: необходимо ждать время переноса, даже если его не было.

5. Параллельный двоичный сумматор (на основе комбинационных).

Формула Cm=AtB, данный сумматор использует модифицированный код.

Недостаток: не хранит значение суммы (после выполнения действия показывает 0), но более быстрый, а также нужно ждать,

когда выполняется перенос.

6. Асинхронный сумматор с последовательным переносом.

Когда каждое Zi=0 значит сумма выполнена, tсум.= e * τ тр

Где e=log2n, n количество, е – длина переноса

9. Сумматор с групповым обходным переносом.

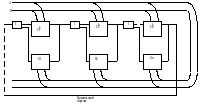
10. Устройства умножения. Общий вид:

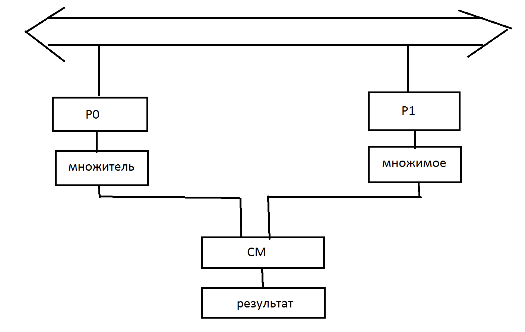
11. Методы ускоренного умножения – краткое описание. Существуют аппаратные и логические способы. Аппаратные – данные способы повышения быстродействия за счёт увеличения кол-ва сумматоров подразделяются на

2 вида: с горизонтальным переносом и с вертикальным переносом Логические – 1. Пропуск такта при равенстве 0 очередного разряда множителя tумн= n(Tсум+Tсдв)……Tумн=N(1/2 Tcум+T сдв)

2. Выполняя умножение с анализом нескольких разрядов (с анализом 2-х разрядов)

12. Методы ускоренного умножения (анализ двух разрядов)

– а – множитель, в- множитель. Умножение по классической схеме, наанализируется одновеменно 2 разряда множителя А(n-1; n)

00 +0 сдвиг на 2 разряда 01 +B сдвиг на 2 разряда 10 +2B сдвиг на 2 разряда 11 13. Ускорен умнож анализ 3-х разрядов 000 0

001 +B

010 +2B

011 +RG3B в спец. Регистре перед началом умнож. формир х3 множимого

100 +4В

101 -RG3B коррект 1

110 -2B коррект 1

111 -B 1 Tумн = n\3(Есум + Tсдвиг) 14. Методы уск. Умножения – алгоритм Бута. + пример множитель анализируется начиная с младших разрядов, и выполн. поиск изменения цифр множителя 000110000111 (помидоры – зло) время изменения цифры множителя из 0 ->1 выполн вычисление множимого из суммы частичного произведения.

При изменении 1->0 происход. Сложение множимого с сум. Частич. произведения

ПРИМЕР

Вычислить 3 × (−4). В этом случае m = 3, r = −4, x = 4, y = 4:

A = 0011 0000 0

S = 1101 0000 0

P = 0000 1100 0

Выполним цикл 4 раза :

P = 0000 1100 0. Крайние два бита равны 00.

P= 0000 0110 0. Арифметический сдвиг вправо.

P = 0000 0110 0. Крайние два бита равны 00.

P = 0000 0011 0. Арифметический сдвиг вправо.

P = 0000 0011 0. Крайние два бита равны 10.

P = 1101 0011 0. P = P + S.

P = 1110 1001 1. Арифметический сдвиг вправо.

P = 1110 1001 1. Крайние два бита равны 11.

P = 1111 0100 1. Арифметический сдвиг вправо.Произведение равно 1111 0100 (−12 в десятичной системе)