12

Общие данные для проектирования.

4-х этажное каркасное здание, без подвала имеет размер в плане 21×54м и сетку колон 7×6.Высота этажей 3м. Стеновые панели навесные из легкого бетона, замоноличиваются совместно с торцевыми рамами, образуя вертикально связевые диафрагмы. Стены подвала из бетонных блоков. Нормативная значение временной нагрузки v= 3500Н/м,

в том числе кратковременная нагрузка 1500Н/м, коэффициент надежности на нагрузке , коэффициент надежности по назначению здания .

Компоновка конструктивной схемы сборного перекрытия

Ригели поперечных рам — трехпролетные, на опорах жестко соединены с крайними и средними колоннами. Плиты перекрытий, предварительно напряженные в двух вариантах, — ребристые и многопустотные. Ребристые плиты принимают с номинальной шириной, разной мм; связевые плиты размещают по рядам колонн; доборные пристенные плиты опирают на ригеля и опорные стальные столики, предусмотренные на крайних колоннах. Многопустотные плиты принимают с номиналь­ной шириной, равной 2200 мм; связевые распорки шири­ной 600 мм размещают по рядам колонн и опирают на ригели и опорные столики на крайних колоннах.

В продольном направлении жесткость здания обес­печивается вертикальными связями, устанавливаемыми в одном среднем пролете по каждому ряду колонн. В поперечном направлении жесткость здания обеспечивается по рамно-связевой системе: ветровая нагрузка через перекрытия, работающие как горизонтальные жесткие диски, передается на торцевые стены, выполняющие функции вертикальных связевых диафрагм, и поперечные рамы. В малоэтажных каркасных зданиях высотой до 5 этажей, как показали исследования, жест­кость поперечных диафрагм намного превышает жесткость поперечных рам, и в этих условиях горизонтальная нагрузка практически передается полностью на диа­фрагмы. Поперечные же рамы работают только на вертикальную нагрузку.

Расчет многопустотной плиты по предельным состояниям первой группы

Расчетный пролет и нагрузки. Расчетный пролет плиты l₀= 5,88 м. Подсчет нагрузок на 1 м² перекрытия приведен в табл. 18.2.

Нормативные и расчетные нагрузки на 1 м² перекрытия

Нагрузка	Нормативная нагрузка, Н/м2	Коэффициент надежности по нагрузке	Расчетная нагрузка, Н/м2
Постоянная: собственный вес многопустотной плиты с круглыми пустотными то же слоя цементного раствора = 20 мм (р = 2200 кг/м3) то же керамических плиток, 6=13 мм (р=1800 кг/м3)	3000 440 240	1,1 1,3 1,1	3300 570 264
Итого Временная В том числе: длительная кратковременная	3680 3500 2000 1500	1,2 1,2 1,2	4134 4200 2400 1800
Полная нагрузка В том числе: постоянная и длительная кратковременная	7180 5680 1500	- - -	8334

Расчетная нагрузка на 1 м при ширине плиты 2,2 м с учетом коэффициента надежности по назначению зда­ния _n= 0,95: постоянная g = 4,134*2,2*0,95 = 8,65 кН/м; полная g+v = 10,134*2,2*0,95=21,2 кН/м; v=6*2,2*0,95= 12,55 кН/м.

Нормативная нагрузка на 1 м: постоянная g=3,68*2,2*0,95 = 7,7 кН/м; полная g+v = 7,18*2,2*0,95 =15 кН/м; в том числе постоянная и длительная 5,68*2,2*0,95=11,87 кН/м.

Усилия от расчетных и нормативных нагрузок.

От рас­четной нагрузки М=( g+v)l²₀/8 = 21,2*5,88²/8=92 кН-м;

Q=( g+v) l₀/2 = 21,2*5,88²/2 = 62 кH. От нормативной пол­ной нагрузки М=15*5,88/8 = 65 кН.м; Q= 15*5,88/2 = 44,1 кН. От нормативной постоянной и длительной на­грузок М = 11,87*5,88²/8 = 52 кН-м.

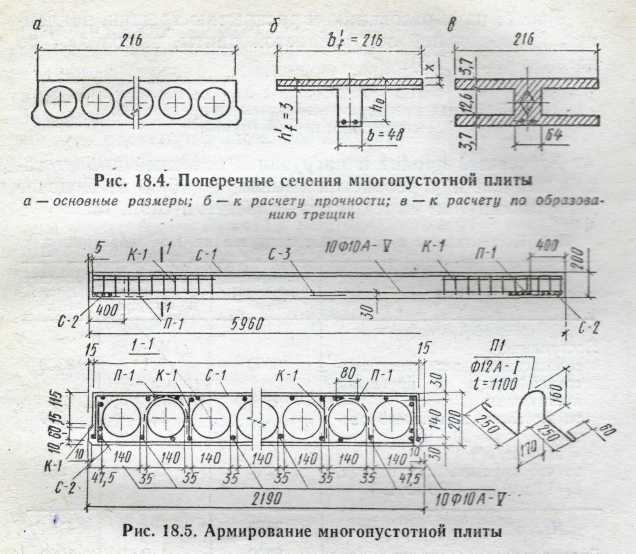
Установление размеров сечения плиты (рис. 18.4).

Высота сечения многопустотной (12 круглых пустот диа­метром 14 см) предварительно напряженной плиты h 588/30 20 см; рабочая высота сечения h₀= h-а=20-3=22 см. Размеры: толщина верхней и нижней полок

(20-14)*0,5 = 3 см. Ширина ребер: сред­них— 3,5 см, крайних — 4,65 см. В расчетах по предель­ным состояниям первой группы расчетная толщина сжа­той полки таврового сечения h_f¹=3 см; отношение h_f¹/h=3/20 = 0,15>0,1, при этом в расчет вводится вся ши­рина полки в_f¹ = 216 см; расчетная ширина ребра в =216-12*14 = 48 см (см. гл. 11).

Характеристики прочности бетона и арматуры.

Многопустотную предварительно напряженную плиту армируют арматурой класса A-V с электротермичес­ким натяжением на упоры форм. К трещиностойкости плиты предъявляют требования 3-й категории. Изделие подвергают тепловой обработке при атмосферном дав­лении.

Бетон тяжелый класса В25, соответствующий напря­гаемой арматуре (см. гл. 2). Согласно прил. 1...4 призменная прочность нормативная R_bn = R_b,ser=18.5 МПа, расчетная R_b = 14.5 МПа; коэффициент условий работы бетона _в2 =0,9; нормативное сопротивление при растя­жении R_bth=R_bt,ser=1.60 МПа, расчетное R_bt=1,05 МПа; начальный модуль упругости бетона Е_b =30000 МПа. Передаточная прочность бетона R_bP устанавливается так, чтобы при обжатии отношение на­пряжений _bP/R_bp 0,75 (см. гл. 2).

Арматура продольных ребер — класса A-V, нормативное сопротивление R_sn = 785 МПа, расчетное сопротивление R_s= 680 МПа; модуль упругости Е=190 000 МПа (см. табл. 1 прил. 5). Предварительное напряжение арматуры принимают равным _sp= 0,6 R_sn= =0,6*785= 470 МПа.

Проверяют выполнение условия (2.22); при электро­термическом способе натяжения р=30+360/l=30+ 360/7=90 МПа; _sp+ р = 470 + 90 = 560< R_sn=785 МПа — условие выполняется.

Вычисляют предельное отклонение предварительного напряжения по формуле (2.25)

_sp=(0,5*90/470)(1+1/ )=0,12

где n= 10-число напрягаемых стержней плиты. Коэффициент точно­сти натяжения при благоприятном влиянии предварительного напря­жения по формуле (2.24) _sp =1— _sp=1-0,12=0,88

При проверке по образованию трещин в верхней зоне плиты при обжатии принимают _sp = 1+0,1 = 1,12.

Предварительное напряжение с учетом точности на­тяжения

_sp =0,8*470=413,6 МПа.

Расчет прочности плиты по сечению, нормальному к продольной оси. М =92 кН-м.

Сечение тавровое с пол­кой в сжатой зоне. Вычисляют

_m=М/ R_bb_f¹h₀²=9200000/[0,9*14,5*216*17²*(100)]=0,11

По табл. 3.1 находят =0,12; х= *h₀=0,12*17=2<3 см — нейтральная ось проходит в пределах сжатой полки; =0,94.

Характеристика сжатой зоны (см. гл. 2): =0,85-0,008R_b=0,85-0,008*0,9*14,5=0,75.

Граничная высота сжатой зоны по фор­муле (2.42)

_R=0,75/[1+ ]=0,55

где _sR =R_s=560+400-413,6=546,4 МПа; _sP=0; в знаменателе принято 500 МПа, поскольку _b2 1.

Коэффициент условий работы, учитывающий сопро­тивление напрягаемой арматуры выше условного преде­ла текучести, согласно формуле (2.44)

_s6= = 1,15-(1,15-1)( )=1,23 ,

где = 1,15 — для арматуры класса A-V; принимают _s6= = 1,15.

Вычисляют площадь сечения растянутой арматуры A_s=M _s6R_s h₀=9200000/1,15 • 680 • 0,94 • 17(100)= 7,4 см² принимают 10 0 10 А-V с площадью A_s = 7,85 см² (прил. 6), рис. 18.5.

Расчет прочности плиты по сечению, наклонному к продольной оси, Q = 62 кН.

Расчет ведут по формулам подглавы 3.5.

Влияние усилия обжатия Р=306 кН (см. расчет предварительных напряжений арматуры плиты): _n=0,1N/R_btbh₀=0,1*306000/1.05*48*17(100)=0,35 0,5.

Проверяют, требуется ли поперечная арматура по рас­чету. Условие: Q_max= 62*10³ 2,5R_btbh₀=2,5*0,9*1,2(100)*48*17= 220*10³Н —удовлетворяется.

При g=g+v/2=8,65+12,5/2=14,93 кН/м=149,3 Н/см и поскольку 0,16 _b4(1- _nR_btb=0,16*1,5(1+0,35)0,9*1.05*48(100)=1469.6 Н/см>146,7 Н/см — принимают с = 2,5 h_о = 2,5*17=42.5 см. Другое условие: Q = Q_max—q₁c = 62*10³—149.3*42.5 = 55.7*10³Н;

_b4 (1+ _n) R_btbh₀=1,5*1,35*0,9* (100)*48*17²/42.5= 59.4*10³ Н>55.7*10³ Н — удовлетворяется также. Сле­довательно, поперечной арматуры по расчету не требу­ется.

На приопорных участках длиной l/4 арматуру уста­навливают конструктивно, 0 4 Вр-1 с шагом s=h/2=20/2=10 см; в средней части пролета поперечная ар­матура не применяется (рис. 18.5).

Расчет многопустотной плиты по предельным состояниям второй группы

Геометрические характеристики приведенного сече­ния. Их определяют по формулам (2.28) — (2.32). Круглое очертание пустот заменяют эквивалентным квадратным со стороной h=0,9d = 0,9*14 = 12,6 см (см. гл. 11). Тол­щина полок эквивалентного сечения h_f¹=h_f=(20-12,6)0,5 = 3.7 см. Ширина ребра 216-12*12,6 =64 см. Ширина пустот 216-64=152 см. Площадь приведенного сечения A_red=216*20-152*12,6=2400 см² (пренебре­гают ввиду малости величиной A_s).

Расстояние от нижней грани до центра тяжести при­веденного сечения y_о=0,5h=0,5*20 = 10 см.

Момент инерции сечения (симметричного)

J_red= = 216*20³/12-152*12,6³/12=118000 см⁴.

Момент сопротивления сечения по нижней зоне W_red = I_red/y₀= 118000/10=11800 см³; то же, по верхней зоне W_red¹ =11800 см³.

Расстояние от ядровой точки, наиболее удаленной от растянутой зоны (верхней), до центра тяжести сечения по формуле (7.31): r=0,85(24 527/3484,8) =5,98 см; то же, наименее удаленной от растянутой зоны (нижней) r_inf =5,98 см; здесь _n =1,6- _br/R_b,ser= 1,6—0,75 = 0,85.

Отношение напряжения в бетоне от нормативных на­грузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы пред­варительно принимают равным 0,75.

Упругопластический момент сопротивления по растя­нутой зоне согласно формуле (7.37), W_pl=yW_red=1,5*11800=17700 см³, здесь =1,5—для двутаврового се­чения при 2<b_f¹/b=b_f/b=216/64=3,5<6. Упругопласти­ческий момент сопротивления по растянутой зоне в ста­дии изготовления и обжатия W'_pl = 17700 см³.

Потери предварительного напряжения арматуры.

Расчет потерь выполняют в соответствии с рекомендаци­ями 2.4. Коэффициент точности натяжения арматуры при этом принимают _sp=1. Потери от релаксации напря­жений в арматуре при электротермическом способе на­тяжения

₁=0,03 _sp=0,03*470=14.1 МПа. Потери от температурного перепада между натянутой арматурой и упорами ₂ = 0, так как при пропаривании форма с упо­рами нагревается вместе с изделием.

Усилие обжатия Pi=A_s( _sp- ₁)=7.85(470-14.1)100=358000 Н=447,307кН. Эксцентриситет этого уси­лия относительно центра тяжести сечения, е_op=10-3=7 см. Напряжение в бетоне при обжатии в соответст­вии с формулой (2.36)

_bp=(358000/2400+ 358000*7*10/118000)/(100)= 3,6 МПа.

Устанавливают значение передаточной прочности бе­тона из условия _bp/ R_bp 0,75; R_bp=3.6/0,75=4,8 0,5В30 (см. подглаву 1.4); принимают R_bp=15 МПа. Тогда отношение _bp/ R_bp=3,6/15= 0.24.

Вычисляют сжимающие напряжения в бетоне на уров­не центра тяжести площади напрягаемой арматуры от усилия обжатия (без учета момента от веса плиты) _bp= (358000/2400+358000•7²/118000)/(100)=2,97 МПа. Потери от быстронатекающей ползучести при _bp/ R_bp=2,97/15=0,19 и при >0,3 _bp=40*0,19=7.92 МПа. Пер­вые потери _los= ₁+ _b=14.1+7.92=22.02 МПа. С учетом _los напряжение _bp=2.9 МПа; _bp/R_bp=0,19, Потери от усадки бетона ₈=35 МПа. Потери от ползучести бетона ₉= 150*0,85*0,19=24 МПа. Вторые потери _los2= ₈+ ₉=35+24=59 МПа. Полные потери _los= _los1+ _los2=22.02+59=81.02 МПа<100, МПа меньше ми­нимального значения.

Усилие обжатия с учетом полных потерь Р₂=A_s( _sp- _los)=7,85 (470-81,02) (100) = 306 000Н=306 кН.

Расчет по образованию трещин, нормальных к про­дольной оси. Выполняют для выяснения необходимости проверки по раскрытию трещин. При этом для элемен­тов, к трещиностойкости которых предъявляют требова­ния 3-й категории, принимают значение коэффициентов надежности по нагрузке _L=1; М=78 кН*м. По формуле (7.3) М М_СГс Вычисляют момент образования трещин по приближенному способу ядровых моментов по форму­ле (7.29)

M_crc=R_bt,_ser W_Pl + M_rp = 1,05*17 700*(100)+3016 000 = 4900000 Н*см = 49кН*м.

Здесь ядровый момент усилия обжатия по формуле (7.30) при _sp=0,9, M_rp=P₂(e_op+r)=0,88*306000 (7+4,2)=3016000 Н*см.

Поскольку М=78>M_crc=68 кН-м, трещины в рас­тянутой зоне образуются. Следовательно, необходим рас­чет по раскрытию трещин.

Проверяют, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении ко­эффициента точности натяжения _sp=1,12 (момент от веса плиты не учитывается). Расчетное условие:

P₁(e_oP-r_inf) R _btpW_pl¹;

1,12*358000 (7-4,2) = 1 122 688 Н*см;

R_btpW_pl¹=1,05*17700(100)=1858 500 Н*см;

1 122 688<1 858 800 — условие удовлетворяется, начальные трещины не образуются; здесь R_btp=1 МПа — со­противление бетона растяжению, соответствующее пере­даточной прочности бетона 12,5 МПа (по прил. 2).

Расчет по раскрытию трещин, нормальных к продоль­ной оси. Предельная ширина раскрытия трещин: непро­должительная а_сгс=0,4 мм, продолжительная а_сгс =0,4 мм (см. табл. 2.2). Изгибающие моменты от нор­мативных нагрузок: постоянной и длительной — М=52 кН-м; полной—М=65 кН-м. Приращение напря­жений в растянутой арматуре от действия постоянной и длительной нагрузок определяют по формуле (7.102)

₈ = (5200 000 — 306 000*15,15)/119 (100) = 3,8 МПа, где z₁ h₀-0,5h_f¹=17—0,5(3,7/2) = 15,15 см— плечо внутренней пары сил; e_sN = 0 — усилие обжатия P приложенное в центре тяжести площади нижней напрягаемой арматуры; W_s=A_sZ₁=7,85*15,15=119 см³— момент сопротивления сечения по растянутой арматуре.

Приращение напряжений в арматуре от действия пол­ной нагрузки

₈=(6500 000 —306 000*15,15)/119(100) — 148 МПа. Вычисляют по формуле (7.47):

ширину раскрытия трещин от непродолжительного действия полной нагрузки

а_сгс1=20 (3,5 - 100 ) _l ( _s/E_s) =

20(3,5— 100*0,0095) 1*1*1 (148/190 000) = 0,09 мм;

где =A_s/bho=7,85/48*17=0,0095; ₁ = 1; = 1; = 1; d=10 мм —

диаметр продольной арматуры;

ширину раскрытия трещин от непродолжительного действия постоянной и длительной нагрузок

а_с¹_гс1= 20 (3,5 — 100* 0,0095) 1*1*1 (39/190 000) = 0,02 мм;

ширину раскрытия трещин от постоянной и длитель­ной нагрузок

а_сге2 = 20 (3,5 — 100-0,0095) 1*1*1,5 (39/190 000) / = 0,03 мм. Непродолжительная ширина раскрытия трещин

а_сге =а_сге1— а_с¹_гс1 + а_сге2 = 0,09 — 0,02 + 0,03 = 0,1 мм< [0,4 мм]; Продолжительная ширина раскрытия трещин

а_сг2с = а_сгс2 = 0,08 мм < [0, мм];

Расчет прогиба плиты.

Прогиб определяют от посто­янной и длительной нагрузок, предельный прогиб f= =2,94 см — согласно табл. 2.3. Вычисляют пара­метры, необходимые для определения прогиба плиты с учетом трещин в растянутой зоне. Заменяющий момент равен изгибающему моменту от постоянной и длитель­ной нагрузок М = 52 кН-м; суммарная продольная сила равна усилию предварительного обжатия с учетом всех потерь и при _sp=1; N_tot=P₂=306 кН; эксцентриситет е_tot=М/N_tot=5200 000/306 000 =17 см; коэффициент _l=0,8 — при длительном действии нагрузок; по формуле (7.75)

_m = 1,6*17 700(100)/(5200000-3016000)=1,3>1 (принимают _m=1); коэффициент, характе­ризующий неравномерность деформации растянутой ар­матуры на участке между трещинами, по формуле (7.74) _s= 1,25—1,04 = 0,21<1.

Вычисляют кривизну оси при изгибе по формуле гл. 2:

l/r= 10^-5

где _b=0,9; v=0,15— при длительном действии нагрузок; А_b=216*З,7=800 см² — при А_s¹ и допущении, что =h_f¹/h₀.

Вычисляют прогиб по формуле (7.131)

f= (5/48)*588²*4,3*10^-5 =1,6 см <2,94 см.

Учет выгиба от ползучести бетона вследствие обжатия бетона по формуле (7.114) несколько уменьшает прогиб.

Расчет по образованию и раскрытию трещин, наклон­ных к продольной оси многопустотной плиты, выполня­ют по данным подглавы 7.2 и 7.3.

Определение усилий в ригеле поперечной рамы

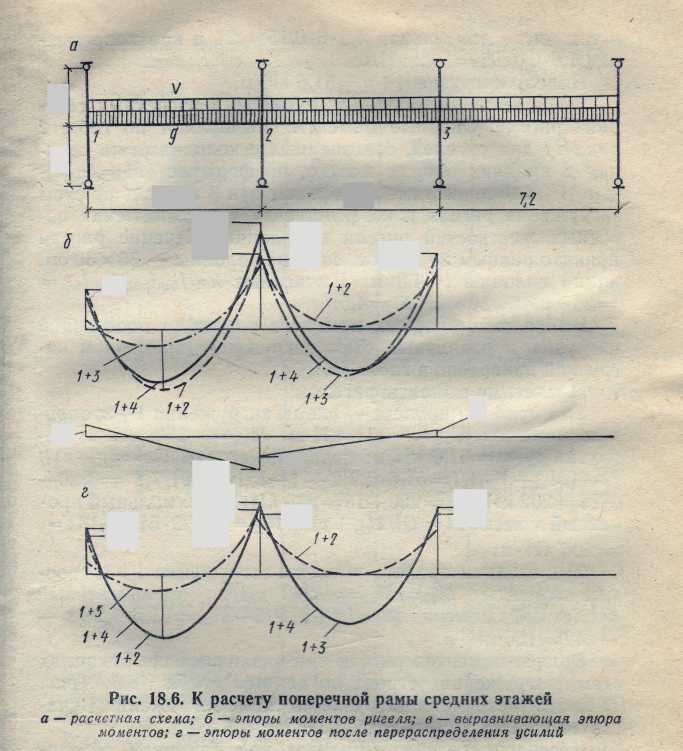
Расчетная схема и нагрузки. Поперечная многоэтаж­ная рама имеет регулярную расчетную схему с равными пролетами ригелей и равными длинами стоек (высотами этажей). Сечения ригелей и стоек по этажам также при­няты постоянными. Такую многоэтажную раму расчле­няют для расчета на вертикальную нагрузку на одно­этажные рамы е нулерьши точками моментов — шарнира­ми, расположенными по концам стоек,—в середине длины стоек всех этажей, кроме первого (см. подглаву 15.3). Расчетная схема рассчитываемой рамы средних этажей изображена на рис. 18.6, а.

Нагрузка на ригель от многопустотных плит считает­ся равномерно распределенной, от ребристых плит при числе ребер в пролете ригеля более четырех — также рав­номерно распределенной. Ширина грузовой полосы на ригель равна шагу поперечных рам, в примере — 6 и.

Схема загружения		Опорные	моменты	кН/м
	М12	М21	М23	М32
	-0,047×72 ×27,4 = - 63	-0,094×72 ×27,4 =-126	-0,087×72 ×27,4 =-118	-118
	-0,056×72 ×23,9 =-66	-0,065×72 ×23,9 =-77	-0,021×72 ×23,9 =-25	-25
	-0,008×72 ×23,9 =+10	-0,029×7,22 ×23,9 =-34	-0,066×72 ×23,9 =-78	-78
	-0,046×72 ×23,9 =-54	-0,106×72 ×23,9 =-124	-0,099×72 ×23,9 =-117	-0,054х23,9х72=-64
Расчетные схемы для опорных моментов	1+2 -129	1+4 -250	1+4 -235	-235
Расчетные схемы для продольных моментов.	1+2 -129	1+2 -203	1+3 -196	-196

Подсчет нагрузок на 1 м² перекрытия приведен в табл. ^ 18.1 и 18.2.

Вычисляют расчетную нагрузку на 1 м длины ригеля.

Постоянная: от перекрытия с учетом коэффициента надежности по назначению зданияу_п=0,95; 4,134*6х0,95=23,6кН/м; отвеса ригеля сечением 0,25х0,6 м (р=2500 кг/см³) с учетом коэффициентов надежности γ_f =1,1 и γ_n=0,95*3,8 кН/м. Итого ν=23,6+3,8= =27,4 кН/м.

Временная с учетом γ_n=0,95; v = 6*4,2*0,95 = 23,94 кН/м,

в том числе длительная 2,4*6*0,95 = 13,68 и кратковремен­ная 1,8-6-0,95 = 10,2 кН/м.

Полная нагрузка g+v = 51.34 кН/м. Вычисление изгибающих моментов в расчетных сечениях ригеля. Опорные моменты вычисляют по табл2, прил 11 для ригелей, соединенных с колоннами средних и крайних опорах жестко, по формуле M .= (αg+βv)l². Табличные коэффициенты α иβ зависит от схемы загружения ригеля и коэффициента k — отношения я погонных жесткостей ригеля и колонны. Сечение ригеля принято равным 25х60 см, сечение колонны — 30х30см, длина колонны / = 3,0 м. Вычисляют k Вычисление опорных моментов ригеля от посте той нагрузки и различных схем загружения временно на­грузкой приведено в табл. 18.3. Пролетные моменты ригеля:

1) в крайнем пролете — схемы загружения 1+2, опор­ные моменты М₁₂= -129 кН-м, М₂₁= -203 кН-м; на­грузка g+v = 51,3 кН/м; поперечные силы Q_i = (g+v )l/ /2—(М₁₂—М₂₁)/ l = 51.3*7/2 - (-129+203)/7 = 179.5 - 10.5=169 кН; Q₂=179.5+10.5=190 кН; максимальный пролетный момент M = Q₁/2{g + v) +M_l2 = 169²/2* 51.3—129 =

=150 кН-м;

2) в среднем пролете — схемы загружения 1+3, опор­ные моменты М₂₃=М₃₂= - 196 кН/м; максимальный пролетный момент М = (g+v)l²/8—М₂₃ = 51,3*7² /8 - 196 = 118кН.м.

Эпюры* моментов ригеля при различных комбинациях схем загружения строят по данным табл. 18.3 тис. 18.6, б). Постоянная нагрузка по схеме загружения 1 уча­ствует во всех комбинациях: 1+2, 1+3, 1+4.

Перераспределение моментов под влиянием образо­вания пластических шарниров в ригеле (11.2, 15.3). Прак­тический расчет заключается в уменьшении примерно на 30 % опорных моментов ригеля М₂\ и M<& по схемам за­гружения 1+4; при этом намечается образование циклицеских шарниров на опоре.

К эпюре моментов схем загружения 1+4 добавляют выравнивающую эпюру моментов так, чтобы уравнялись опорные моменты М₂₁=М₂₃ и были обеспечены удобства армирования опорного узла (рис. 18.6, в). Ординаты выравнивающей эпюры моментов: ΔМ₂₁ = 0.3*250 = 75 кН-м ; ΔМ₂₃ = 235-175 = 60 кН-м; при этом М₁₂= М₂₁ /3= -75/3 = - 25 кН-м; М₃₂ = М₂₃= 0 кН-м

Разность ординат в узле вырав­нивающей эпюры моментов передается на стойки. Опор­ные моменты на эпюре выравненных моментов составля­ют: М₁₂=(-63 - 54) - 25= 142 кН-м; М₂₁ = - 250 + 75= - 175 кН-м; М₂₃ = - 235+0 = - 235 кН-м; М₃₂ = - 118 – 64 = 182 кН-м (рис. 18.6,г).

Пролетные моменты на эпюре выровненных моментов могут превысить значения пролетных моментов при схемах загружения 1+2 и 1+З, тогда они будут расчетными.

Опорные моменты ригеля по грани колонны. На сред­ней опоре при схеме загружения 1+4 опорный момент ригеля по грани колонны не всегда оказывается расчет­ным (максимальным по абсолютному значению). При большой временной нагрузке и относительно малой по­гонной жесткости колонн он может оказаться расчетным при схемах загружения 1+2 или 1+3, т. е. при больших отрицательных моментах в пролете. Необходимую схе­му загружения для расчетного опорного момента риге­ля по грани колонны часто можно установить сравнитель­ным анализом значений опорных моментов по табл. 18.3 и ограничить вычисления одной этой схемой. Ниже при­ведены вычисления по всем схемам.

Опорный момент ригеля по грани средней колонны слева М(21),1 (абсолютные значения);

1) по схемам загружения 1 + 4 и выравненной эпюре мо­ментов М(21)1==М₂₁—Q₂h_Col2 = 175—190-0,3/2 = 146,5 кНМ;

Q₂=(g+ v)l/2— (M_2i—M_l2 )/l=51.34 * 7/2 - (- 175+ + 142)/7 = 179.7 + 4.71 = 184.41 кН; Q_i = 179.—4.71=174.9 кН;

2) по схемам загружения 1+3 М₍₂₁₎₁= 160 – 128* 0,3/2 = 140 кН-м; Q₂=gl/2—_:(М₂₁—М₁₂)/l= 27.4 * 7/2 - (- 160 + 53)/7= 95+33.28=128 кН

3) по схемам загружения 1+2 М_(21),1= 203 – 190*0,3 /2 = 174,5 кН-м.

Опорный момент ригеля по грани средней колонны справа М_(23),1

1) по схемам загружения 1+4 и выровненной эпюре моментов М₍₂₃)₁ = M₂₃—Q_hCol2 = 235 – 186*0,3/2 =210 кН-м; Q = 51*7/2 - (- 235 + 182)/7 = 186 кН;

2) по схемам загружения 1+2 M_(23),i<M₂₃=142 кН м. Следовательно, расчетный опорный момент ригеля по

грани средней опоры М=210 кН • м.

Опорный момент ригеля по грани крайней колонны и по схеме загружения 1+4 и выровненной эпюре моментов M_(I2),₁= M₁₂ - Q_{1 hCo/l2} =142 – 184*0,3/2=114 кН-м.

Поперечные силы ригеля.

Дли расчета прочности по сечениям, наклонным к продольной оси, принимают значения поперечных сил ригеля, большие из двух расчетов: упругого расчета и с учетом перераспределения моментов. На крайней опоре Q_i=184 кН, на средней опоре слева по схеме загружения 1+4 Q₂=51*7/2 – (-250 +117)/7 =197 кН. На средней опоре справа по схемам загружения 1+4 Q₂=51* 7/2 - (- 235 +146)/7 =235 кН.