3. Средняя скорость, расход жидкости. Уравнение неразрывности потока.

В пределах живого сечения потока в круглой трубе скорость жидкости изменяется от нулевого значения у стенки трубы (точки А,В, рис.7) до максимального значения в точке С на оси потока.

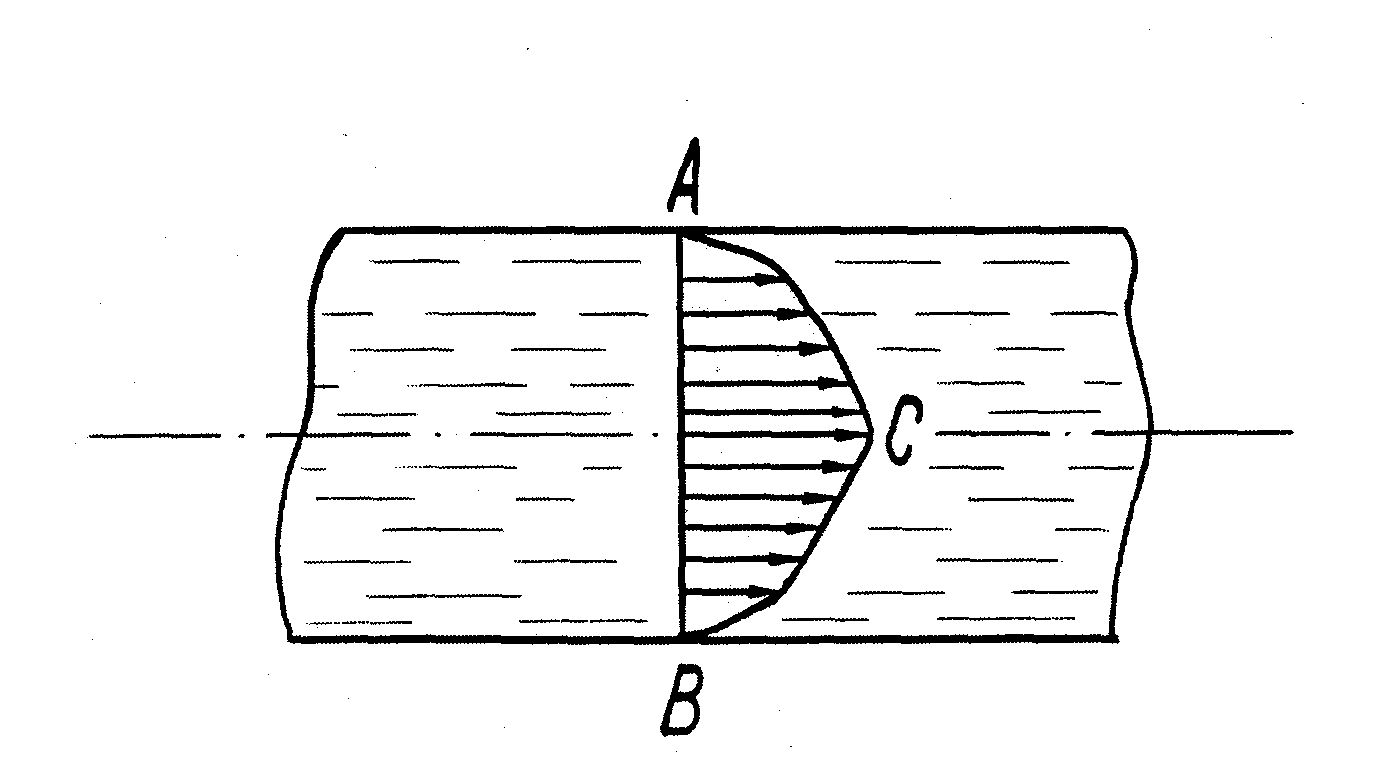
Рисунок 7.Эпюра распределения скоростей потока в круглой трубе.

В практических расчётах пользуются средней скоростью движения жидкости.

Для уяснения этого понятия рассмотрим случай установившегося движения, исходя из предположения, что скорость жидкости одинакова во всех точках живого сечения, (рисунок 8).

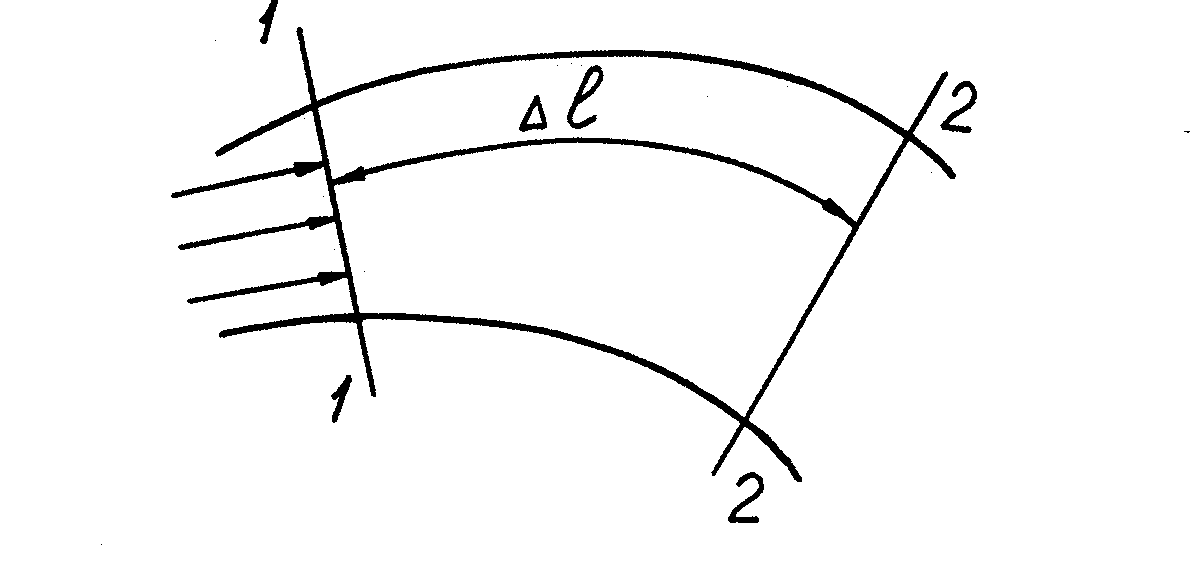
Рисунок 8.Схема для определения средней скорости потока

Рассматриваемый поток имеет живое сечение ω, которое занимает начальное положение 1-1. Через некоторый промежуток времени Δt все точки этого сечения переместятся в положение 2-2, находящегося от положения 1-1 на расстоянии А1.

Через сечение 1-1 за время Δt прошёл объём жидкости

V=ωΔ1

Тогда расход жидкости в сечении 1-1 будет равен

Но отношение есть средняя скорость жидкости в сечении 1 -1

Q = ωV_ср (1)

Отсюда находим среднюю скорость

Таким образом, средней скоростью потока называется фактическая скорость, при которой данное сечение пропускает количество жидкости, равное действительному расходу в этом сечении.

Уравнение (1) называется уравнением расхода и может служить для определения одной из трёх входящих в него величин, по двум другим данным.

Расходом потока называется количество жидкости, протекающей через жи­вое сечение потока в единице времени.

Расход может быть выражен в единицах:

-объёма (м³/с)

-массы (кг/с)

-веса (н/с)

Для вывода уравнения неразрывности потока выделим в установившемся потоке несжимаемой жидкости некоторый отсек, заключённый между двумя произвольными сечениями 1-1 и 2-2 (рис.9). В этот отсек в единицу времени через сечение 1-1 втекает объём жидкости, равный

А через сечение 2-2 из него вытекает объём жидкости, равный

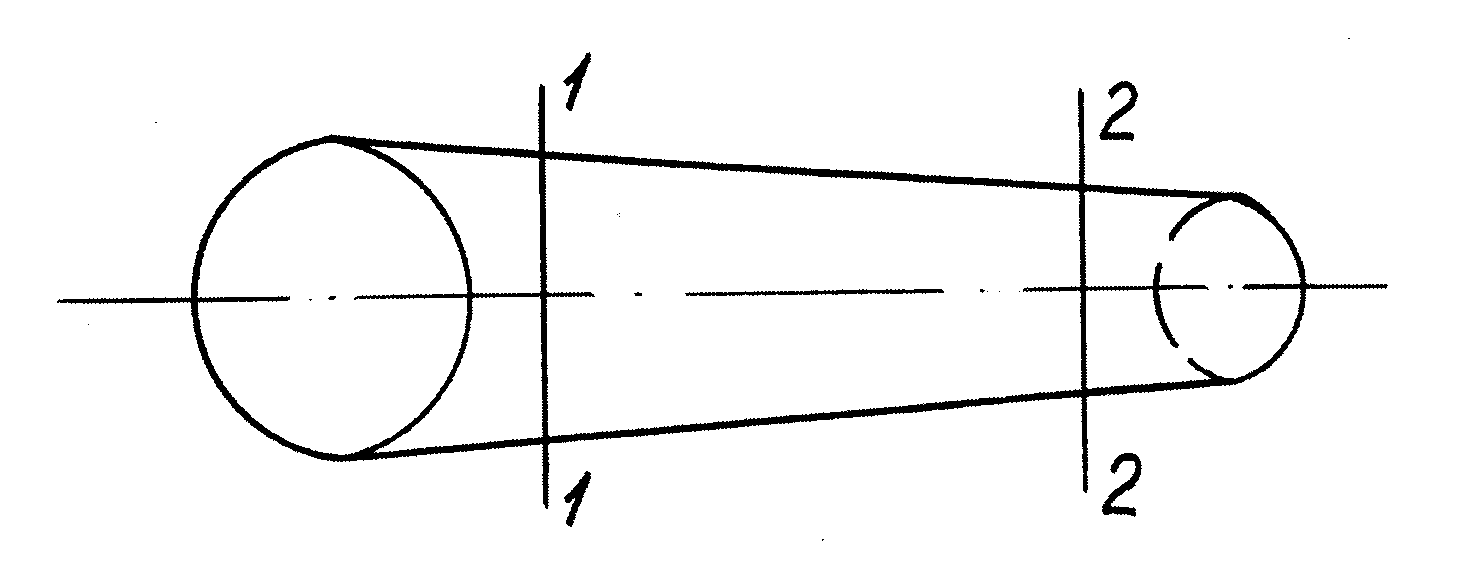
Рисунок 9.К выводу уравнения неразрывности потока.

Так как жидкость несжимаема и поток установившийся, то в потоке невозможно образование незаполненной жидкостью пространства—пустот, то есть будем считать, что соблюдается условие сплошности или неразрывности движения. Учитывая это, можно сделать вывод, что объём жидкости, входящий в отсек за любой промежуток времени, равен объёму жидкости, выходящему из отсека за тот же промежуток времени.

Таким образом, Q₁= Q₂

Или ω₁V₁ = ω₂V₂

Подобные уравнения можно составить для любых сечений потока. В более общем виде можно записать, что всюду вдоль потока

Q= ω₁V₁= ω₂V₂ =… ω_nV_n =const

Это уравнение называется уравнением неразрывности потока.

Оно представляет собой гидравлическое уравнение постоянства расхода.

Данное уравнение показывает, что при установившемся движении, несмотря на изменение средних скоростей и площадей живых сечений по длине потока, расход в нём остаётся постоянным. Из уравнения вытекает следующая зависимость

Эта зависимость показывает, что средние скорости всегда обратно пропорциональны площадям соответствующих живых сечений.

Заключение

Настоящий лекцией положено начало изучения кинематики и гидродинамики жидкости. В лекции рассмотрены основные понятия и определения гидродинамики: задачи, которые решает гидродинамика; виды движения жидкости; поток жидкости и его основные элементы; средняя скорость и расход жидкости. Дан вывод уравнения неразрывности потока.

Четкое знание этих определений является необходимым условием для успешного изучения гидродинамики.