В начале лекции, говоря о вакуумметрическом давлении мы написали уравнение

Р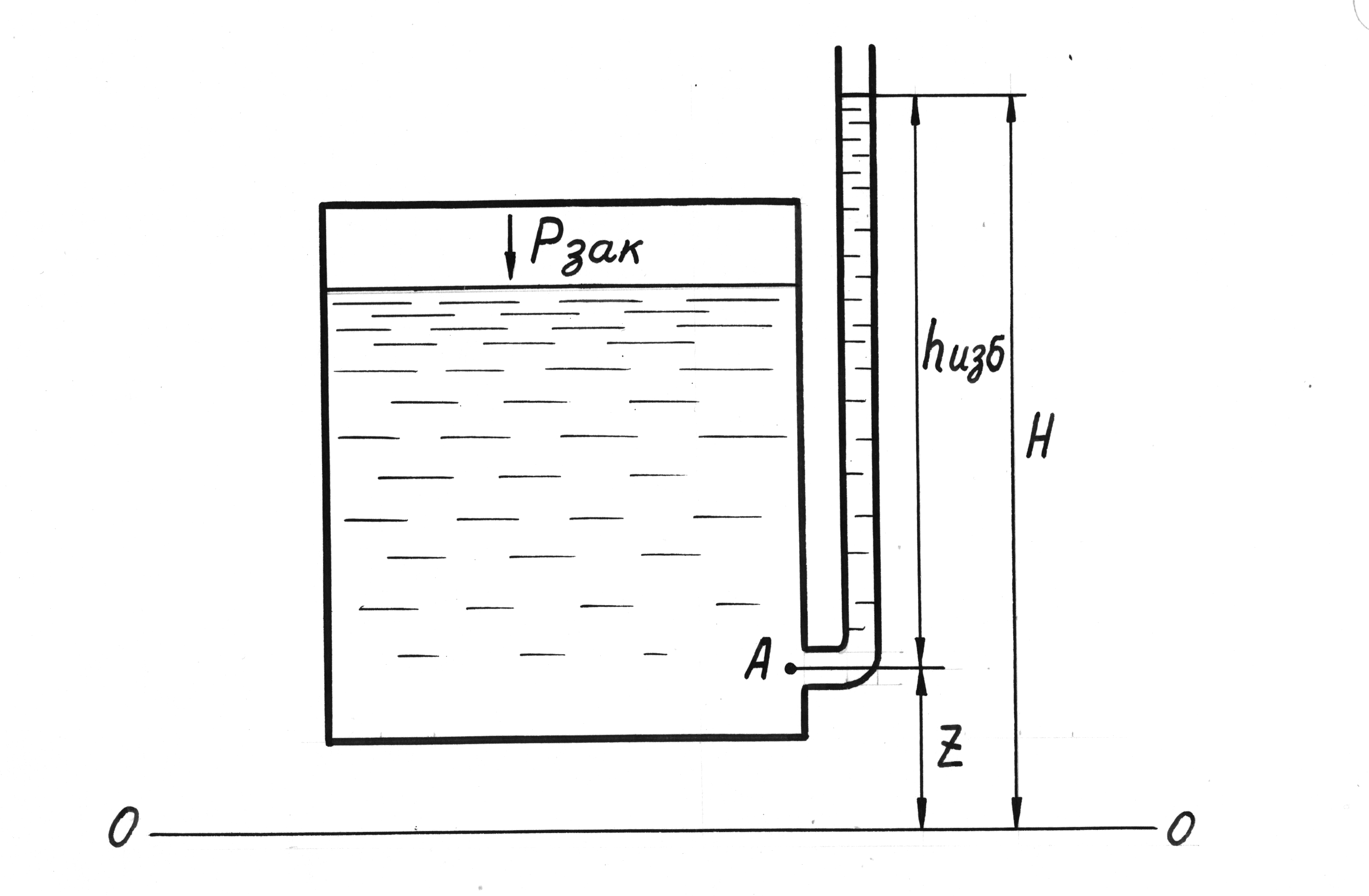 _зак = Р_а - Р_абс

Рисунок 12

Отсюда, разделив обе части уравнения на ρq, получим:

,

где

Окончательно получим значение вакуума:

Р_вак =

Заключение

В лекции рассмотрены силы, действующие в покоящейся жидкости; виды гидростатического давления. Выведено основное уравнение гидростатики, дано определение Закона Паскаля, которое имеет большое практическое значение в технике. Большое внимание уделено понятиям: геометрическая высота, пьезометрическая высота, гиростатический напор, вакуум. Эти понятия необходимо твердо знать для решения практических задач, которые будут встречаться при дальнейшем изучении специальных дисциплин.

ЛИТЕРАТУРА

1. Е.З.Рабинович. " Гидравлика ". Учебник. М. "Недра". 1987.

2. Р.Р.Чугаев. " Гидравлика ". Учебник. Л. Энергоиздат. 1982.

3. П.К. Германович «Гидравлика в нефтегазовом деле". Учебное пособие. Ульяновск. УВВТУ. 2004.

Лекция 3. Гидростатическое давление жидкости на поверхности.

1. Сила гидростатического давления жидкости

на плоскую поверхность.

Задача определения силы гидростатического давления на плоскую поверхность сводится к определению равнодействующих сил гидростатического давления, приложенных к элементарным площадкам, составляющим рассматриваемую поверхность.

Допустим, что плоская стенка, ограничивающая некоторый объем покоящейся жидкости, наклонена к горизонту под некоторым произвольным углом α (рисунок 1)

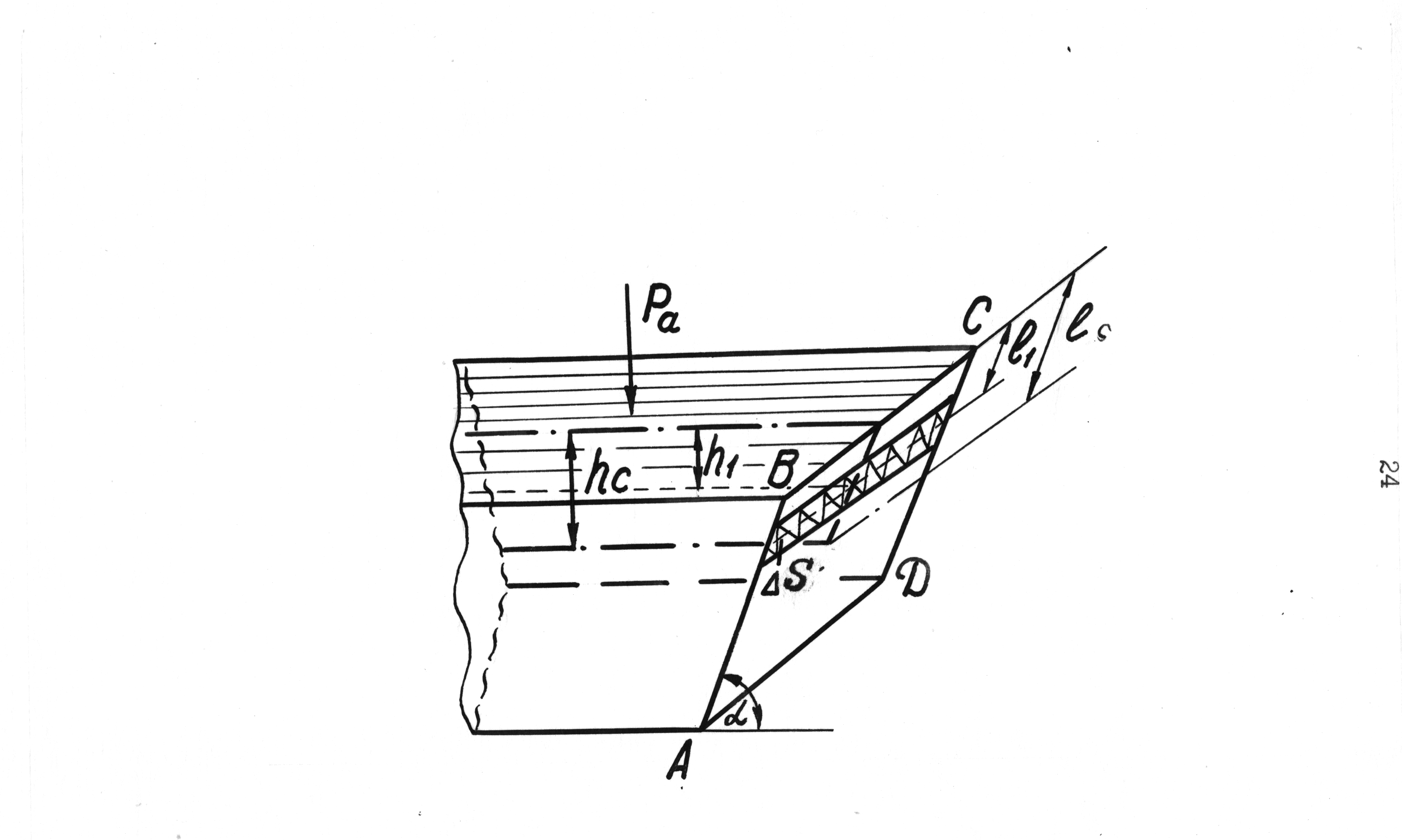
Рисунок 1

Условимся, что плоская стенка АБСД полностью соприкасается с жидкостью. Площадь стенки АБСД разобьем на ряд элементарных полосок площадью S каждая.

Давление в любой точке, лежащей на оси элементарной площадки по основному управлению гидростатистики равно

Р_абс=Р_а+ρgh₁ (1)

Ввиду малой ширины S можно считать, что давление такой величины будет во всех ее точках.. Сила давления на всю элементарную площадку S будет

Р_абс=(Р_а+ρgh₁) S (2)

Для нахождения силы гидростатического давления на всю смоченную поверхность стенки АБСД просуммируем элементарные силы давления

Р_абс= Р_абс= ∆S+ρgh₁ S

Р_абс=Р_а∑∆S+ρg∑h₁· S

Учитывая, что

∑∆S=S и h₁=ℓ₁ Sinα

Р_абс=Р_аS+ρg∑ℓ₁ Sinα ∆S=

Получим

=Р_аS+ρg Sinα ∑ℓ₁ ∆S

∑ℓ₁∆S –есть, как известно из механики, статический момент площади смоченной поверхности относительно линии уреза жидкости (линии БС), равным

₁ΔS= S _с

(площади, умноженной на расстояние до центра тяжести площади).

Тогда Р_абс= Р_аS+ ρq Sinα S _с

а Sinα = h_с и следовательно

Р_абс = Р_аS + ρq h_с S

Окончательно

Р_абс = (Р_а + ρq h_с) S (3)

Так как угол α был взят произвольно, то найденное выражение действительно для любого положения плоской стенки – от горизонтального до вертикального.

Таким образом, сила гидростатического давления на плоскую поверхность равна произведению гидростатического давления в центре тяжести смоченной поверхности на площадь этой поверхности.

Для технических расчетов обычно определяют не абсолютное давление, а избыточное давление на поверхности, так как действие атмосферного давления на свободную поверхность жидкости и на внешнюю не смоченную поверхность взаимно уравновешиваются.

Тогда Р_изб = ρq h_с S (4)