Лапченко Д.А.

Методические указания

по выполнению контрольной работы по дисциплине

«Коммерческий риск и теория принятия решений»

для студентов заочной формы обучения

Задача 1. Обоснование решений в условиях риска

Степень риска коммерческого проекта возможно оценить с помощью коэффициента вариации, который характеризует относительный разброс случайной величины (например, в виде ожидаемой прибыли от реализации проекта):

.

Чем больше коэффициент вариации, тем больше неопределенность в отношении ожидаемой прибыли и, следовательно, тем больше степень риска коммерческого проекта. Причем принято выделять следующие уровни риска:

1. Kv < 10% - малая степень риска;

2. Kv = (10-25)% - средняя степень риска;

3. Kv > 25% - высокая степень риска.

Математическое ожидание случайной величины (например, ожидаемый размер прибыли) и среднее квадратическое отклонение могут быть рассчитаны следующим образом:

• если имеется полная информация о распределении случайной величины –

МО = ∑p_i∙x_i ,

где x_i – прогнозная оценка случайной величины в i-м состоянии;

p_i – вероятность i-й прогнозной оценки;

σ = ,

• если известны только размах колебаний случайной величины (x_min и x_max) и соответствующие вероятности (p_min и p_max) – расчет производится на основе предположения о β-распределении случайной величины -

МО = ;

σ = ,

или σ = (если вероятности неизвестны).

Для решения задачи MO и σ ожидаемой среднегодовой прибыли от реализации коммерческих проектов определяется на основе приближенных соотношений для -распределения.

Задача 2. Обоснование решений в условиях неопределенности

Выбор рационального проекта (стратегии, альтернативы) осуществляется с использованием различных критериев для оптимизации решений в условиях неопределенности.

Разработкой рекомендаций для выбора наилучшего варианта действий в условиях неопределенности занимается теория статистических решений. Эта математическая теория рассматривает игры с природой, в которых под природой понимаются объективные обстоятельства, внешняя среда. Считается, что природа сознательно не противодействует игроку. Условие задачи представлено в виде матрицы выигрышей (a_ji) игры с природой:

Матрица игры

Si xj	S1	S2	…	Sn
x1	a11	a12		a1n
x2	a21	a22		a2n
…	…
xm	am1	am2		amn

x_j – стратегии сознательного игрока, ;

S_i – состояния природы, ;

a_ji – выигрыш сознательного игрока при использовании им стратегии x_j, если состоянием природы будет S_i.

1. Критерий Лапласа.

Данный критерий предполагает равновероятность состояний внешней среды и рекомендует выбор стратегии с максимальным средним выигрышем:

К_Л = .

Вероятности состояний природы p_i равны между собой:

.

2. Критерий Байеса.

Этот критерий учитывает вероятности состояний природы и рекомендует выбор стратегии с максимальным среднеожидаемым выигрышем:

К_Б = , .

3. Критерий Вальда (максиминный критерий, критерий крайнего пессимизма, критерий наибольшей осторожности).

Данный критерий ориентируется на худшее состояние внешний среды и рекомендует выбор стратегии с максимальным гарантированным выигрышем в таких условиях:

К_В = .

4. Критерий Сэвиджа (минимаксного риска).

Критерий минимаксного риска ориентируется на самую неблагоприятную обстановку и рекомендует выбор стратегии с минимальным риском:

К_С = .

Для использования данного критерия необходимо перейти от матрицы выигрышей к матрице рисков.

Риск (r_ji) – разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием природы будет состояние S_i, и выигрышем, который игрок получит, не имея этой информации при использовании стратегии x_j:

, (при заданном i).

5. Критерий Гурвица (компромиссный критерий, критерий пессимизма-оптимизма).

Этот критерий учитывает индивидуальные предпочтения сознательного игрока к пессимизму и оптимизму. Для его использования необходимо задать значение коэффициента пессимизма α, α [0,1]:

К_Г = .

Возможны следующие характерные случаи использования критерия Гурвица:

1. если  = 1, то

К_Г¹ = .

В этом частном случае критерий Гурвица совпадает с критерием Вальда (крайнего пессимизма).

2. если  = 0, то

К_Г⁰ = .

В этом частном случае критерий Гурвица совпадает с критерием крайнего оптимизма.

3. если  = 0,5, то

К_Г^0,5 = .
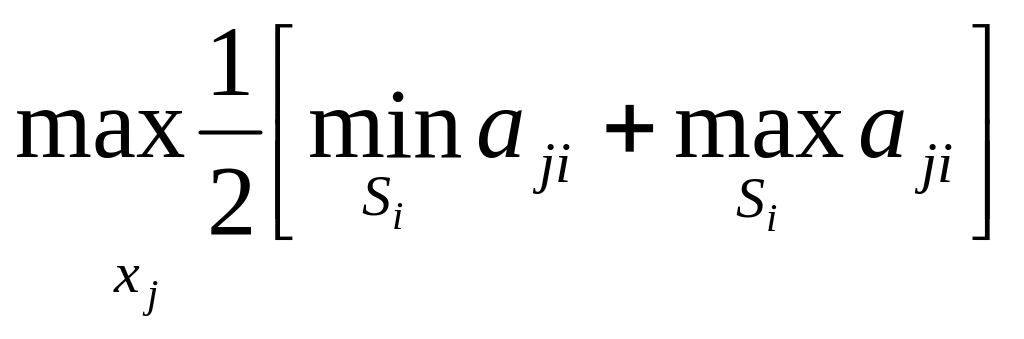