2. Практична частина

Вправа 1.

Ряд збіжний оскільки

якщо

Впарва 2.

Дослідити на збіжність ряд

Зробимо наступну оцінку:

Якщо то не виконується умова (3), отже, розглянутий ряд розбіжний.

Для рядів з монотонними членами необхідну умову збіжності можна підсилити наступним чином.

Вправа 3.

Умова є лише необхідною для збіжності ряду з монотонною послідовністю членів. Дійсно, для ряду виконується умова (4), але він є розбіжним. Справді,

отже, послідовність частинних сум ряду є необмеженою.

Вправа 3.

Приймаючи до уваги, що , починаючи від деякого номера, маємо нерівності

Таким чином для нашого ряду існує збіжний мажорант ний ряд . Отже, ряд збіжний.

Вправа 4.

Нехай (де фігурує п-1 коренів) і Доведемо рівність Маємо: . Припустимо, що Тоді . Тепер можемо оцінити а_п:

Ряд мажорується збіжним рядом , і він також збіжний.

Вправа 5.

Дослідимо на збіжність наступні ряди:

Ознаку Даламбера не можна застосувати, бо , і границя не існує. За ознакою Коші ряд збіжний, бо

.

Вправа 6.

Дослідимо збіжність наступних рядів:

Нехай (a_n)=(1, 1, 1, -3, 1, 1, 1, -3, 1, …), . Тоді (A_n)=(1, 2, 3, 0, 1, 2, 3, 0, 1, …) – обмежена послідовність, а послідовність (b_n) монотонно прямує до 0. Збіжність ряду випливає.

Вправа 7.

Знайдемо суму ряду Лейбніца, який збіжний. Позначимо через L_k k-ту частинну суму цього ряду. На підставі маємо:

Отже, сума ряду Лейбніца дорівнює ln2.

За допомогою частинних сум ряду Лейбніца легко знайти значення ln2 із заданою точністю. Наприклад, з точністю 0, 1 число ln2 наближається числом .

Вправа 7.

Дослідимо на збіжність наступний ряд:

Послідовність монотонно збігається до нуля.

На підставі результатів послідовність із загальним числом

Теж прямує до нуля. З іншого боку,

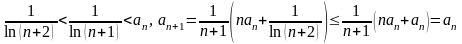
Тобто послідовність (a_n) монотонно спадна. Отже, наш ряд є рядом лейбніцівського типу, тому він збігається.

Вправа 8.

Розглянемо ряд

x ϵ R.

Нехай при деякому k ϵ Z. Тоді

де 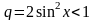, тобто ряд мажорується збіжним геометричним рядом. При вказаних значеннях x ряд (7) абсолютно збігається.

Нехай при деякому k ϵ Z. Тоді і ряд (7) умовно збігається як ряд лейбніцівського типу.

Якщо при всіх значеннях k ϵ Z, то . У цьому випадку загальний член ряду не прямує до нуля, отже, ряд розбігається.

Вправа 9.

 Дослiдимо на збiжнiсть геометpичний ряд     

 а) Hехай  . Тодi  , i pяд pозбiжний. Зокpема, якщо  , то маємо pяд   Тоді   і  . Якщо ж  , то маємо pяд     -на часткова сума якого   . Очевидно, що гpаниця     не iснує. 

б) Hехай   . Вiдома фоpмула суми    пеpших членiв геометричної прогресії   Тоді   .  Отже, pяд   збiгається i його сума   

Вправа 10.

 Ряд  за ознакою Лейбніца збігається . Цей ряд відрізняється від гармонійного тільки знаками членів парних номерів.

Вправа 11.

Ряд   збігається за ознакою Лейбніца. Якщо покласти його суму   наближено рівною сумі перших шести членів цього ряду, то отримаємо похибку, абсолютна величина якої менша, ніж