1.3. Асоціативні і комутативні властивості рядів

Скінченні суми дійсних чисел мають асоціативну і комутативну властивості, тобто значення суми не змінюється при групуванні і переставленні доданків. Інакше ведуть себе нескінченні суми, тобто ряди.

Означення. Нехай (m_k) – строго зростаюча послідовність натуральних чисел і

(1)

• довільний числовий ряд.

Покладаємо

b₁: = a₁+…+ a_m1 , b_k+1:=am_k+1+…+ a_mk+1, k N

і утворюємо новий ряд

=(a₁+…+a_m1)+(am_k+1+…+a_m2)+…. (2)

Кажемо, що ряд (2) одержаний з ряду (1) розстановкою дужок, а ряд (1) одержується з ряду (2) розкриттям дужок.

Теорема 1. У збіжному ряді (1) розстановкою дужок: ряд (2) також збіжний має ту саму суму, що й вихідний ряд (1).

Доведення. Послідовність (B_k) частинних сум ряду (2) є послідовністю (A_n) частинних сум ряду(1):

B_k = b₁+…+b_k=( a₁+…+ a_m1)+…+(a_mk-1⁺¹+…+a_mk)=A_mk .

Оскільки послідовність (A_n) збіжна , то , що й стверджується в теоремі.

Теорема 2. У збіжному ряді (2)допустиме розкриття дужок, тобто із збіжності ряду (2)випливають збіжність ряду (1) і спів падіння їх сум, якщо виконується одна з наступних умов:

1. ряд (1) збіжний;

2. доданки, які визначають b_k , мають одинакові знаки;

3. послідовність(m_k+1-m_k) обмежена і lim a_n=0.

Доведення. У випадку 1) твердження про рівність сум рядів(1) і (2) випливає із теореми 1.

Нехай виконується умова 2) і B=lim B_k – сума ряду (2). Як і в доведенні теореми 1, A_mk=B_k B ghb k . виберемо довільне >0. Тоді існує таке K N , що

B- <A_mk<B+ (3)

при всіх k  K. Ці нерівності виконуються також для всіх A_n з n  m_k, бо внаслідок знакосталості членів а_п при т_к< п  т_к+1 частинні суми А_п находяться між A_mk і A_mk+1 . Отже, lim А_п = B.

У випадку 3) міркуємо аналогічно. Нехай т_к+1 - т_к  М при всіх k N. Згідно з умовою lim а_п = 0 існує таке N N, що при п . Якщо n  N₁: = max N, m_k ,то при т_к< п  т_к+1. Отже, В-2 при всіх n  N₁ . Це означає, що lim А_п = B

Зауваження. Асоціативна властивість, тобто можливість групування членів ряду має місце лише при певних обмеженнях. Прикладами таких обмежень є умови 1)-3) теореми 2.

Введемо позначення max а_п , 0, а_п= max -а_п , 0.

Тоді мають місце співвідношення

0. . , 0  , а_п= - , = + . (4)

Означення. Ряди

і (5)

Називаються відповідно рядами додатніх і відємних членів ряду(1).

Зауваження. Серед членів ряду (6) є нульові , але, пропускаючи їх, ми не знімаємо ні збіжність, ні суми рядів (див. теорему 6). Після викреслення нульових членів, в рядах (6) залишаються відповідно додатні і відємні члени ряду (1).

Теорема 3. Ряд (1) абсолютно збіжний тоді і тільки тоді, коли збіжні ряди (6), причому

- = (7)

+ =   (8)

Якщо ряд (1)умовно збіжний, то ряди (6) мають суму + .

Доведення. Якщо ряд (1) абсолютно збіжний, то ряди (6) теж збіжні, як мінорантні ряди по відношенню до (див. (4)).

Якщо ряди (6) збіжні, то внаслідок рівностей із (5) для частинних сум відповідних рядів мають місце рівності

де - частинна сума ряду . Переходом до границі в цих рівностях дістаємо, що ряди збіжні і справедливі рівності (7) і (8).

Нехай ряд умовно збігається. Припустимо, що ряд збігається. Тоді внаслідок рівностей збігається також ряд . Аналогічно, із збіжності ряду і рівностей випливає, що збіжним є також ряд . В обох випадках ряди (6) збіжні, отже, згідно з доведеним вище, ряд абсолютно збігається. Ми прийшли до суперечності. Теорема доведена. □

Означення. Нехай – деяка бієкція. Будемо казати, що ряд

отримано за допомогою п ереставлення членів ряду (1).

Теорема4 (Діріхле). В абсолютно збіжному ряді (1) допустіме довільне переставлення членів: ряд (9) також збігається абсолютно і має ту ж суму, що й ряд (1).

Доведення. Припустимо спочатку, що ряд (1) додатний. Частинні суми рядів (1) і (9) позначатимемо відповідно символами , а їх суми– відповідно буквами А і A'. Нехай Тоді

(10)

Із збіжності додатного ряду (1) випливає, що його послідовність частинних сум обмежена числом А. Згідно з (10), цим числом обмежена також послідовність 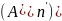. Тому ряд (9) збіжний до такої суми A', що A' A (теорема 1).

Але ряд (1) можна отримати із ряду (9) перестановкою членів, яка задається бієкцією, оберненою до (k_n). Тоді на підставі доведеного маємо нерівність A A'. Остаточно: A' A.

Очевидно, доведене твердження справедливе і для від'ємних рядів.

Нехай тепер ряд (1) має довільні члени, причому він абсолютно збіжний.

Можемо користуватися теоремою 3. Оскільки ряди i знакосталі, для них припустиме переставлення членів. На підставі теореми 3 і рівності типу (7) ряд (9) абсолютно збігається і має суму, рівну

Теорема 5 (Рімана) Нехай ряд (1) збігається умовно і . Тоді існує таке переставлення членів, що ряд (9) має суму S. Члени ряду (1) можна переставляти й так, щоб ряд (9) немав суми.

Доведення проведемо лише у випадку S є R. Внаслідок теореми 3 ряди (6) мають суму + .

Будемо вважати, що ряд (1) не має нульових членів. Із рядів (6) вилучимо нульові члени і одержані ряди позначимо відповідно через . Нехай – послідовності частинних сум цих рядів. Тоді (див. теорему 3 і зауваження перед цією теоремою).

Будуємо дві послідовності (р_n) і (q_n) рекурентним способом, користуючись теоремою 4.

Ряд типу (9) задаємо наступним чином:

Очевидно, ряд (11) отримано із ряду (1) переставленням членів ряду (1). Доведемо, що ряд (11) збігається до суми S. Нехай (S_n) – послідовність частинних сум ряду (11). Тоді при k, n N.

,

,

,

Оскільки при , то із останніх нерівностей випливає, що .