Вднз «Ужгородський національний університет» Інститут післядипломної та доуніверситетської підготовки

Курсова робота

на тему:

«Ознаки збіжності числових рядів

з членами довільних знаків»

Студентки І курсу ІПОДП

напрям підготовки – математика

Філіп Наталії Василівни

Керівник: доц. Поляк Іван Йосипович

Національна шкала____________________

Кількість балів___Оцінка: ECTS________

Члени комісії:

______________________________________________________________________________________________________________________________

Ужгород – 2014

Зміст

Вступ……………………………………………………………….….. 3

Числові ряди. Загальні поняття про ряди.

1. Теоретична частина…………………………………………………... 6

1.1. Ряди з додатними членами

1.3. Ознаки збіжності довільних рядів. Абсолютна збіжність

1.3. Асоціативні і комутативні властивості рядів

2. Практична частина…………………………………………………...16

Висновок……………………………………………………………... 21

Список використаної літератури…………………………………... 22

Вступ Числові ряди. Загальні поняття про ряди

При розв’язуванні багатьох задач виникають нескінченні послідовності. Розглянемо класичні методи сумування нескінченних послідовностей.

Означення. Нехай (а_n) — числова послідовність, тобто послідовність в R. Упорядкована пара ((а_n), (A_n)) двох послідовностей (а_n) і (A_n) називається

числовим рядом, якщо А_n = a₁ + ... + a_n , n N (зокрема, A₁ = a₁). Для позначення ряду ((а_n), (A_n)) вживаються також символи

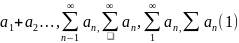
Змінна n в позначеннях (1) уявна, тобто може замінятися будь-якою іншою буквою k, 1, m, i , j і т.д.

Члени послідовності (а_n) називаються членами ряду, а члени послідовності (А_n) - частинними сумами ((а_n), (А_n)); а_к і А_к – відповідно к-тий член і k-ma частинна сума ряду (1).

Як і для послідовностей, можна відрізняти члени від значення членів:

(n, а_n) - n-ий член послідовності (а_n), або ряду (1), а число а_n – значення n-ого члена послідовності (а_n), або ряду (1). Аналогічне зауваження маємо для (А_n). Однак, на практиці не відрізняють n-ий член від значення n-ого члена, n-ну частинну суму – від значення n-ної частинної суми ряду.

Часто рядом називають символ - позначення ряду. Ми надаємо перевагу більш змістовному означенню, яке подано вище. Позначення (1) подібні до символів скінченних сум, тому вони більш природні ніж позначення

((а_n), (А_п)). Слід зазначити, що в позначеннях (1) явно не фігурує (А_n), проте члени цієї послідовності легко поновлюються за допомогою (а_n): a₁ + ... + a_n, N. Навпаки, члени ряду виражаються через частинні суми так: a₁ = А_1, a_n+1 = А_п+1 - А_п , N.

Означення. Сумою двох рядів ((a_n), (А_n)) і ((b_n), (В_n)) називається ряд ((a_n + b_n), (А_n + В_n)). Добутком ряду ((а_n), (А_n)) на число c називається ряд ((са_n), (сА_п)). Протилежним до ряду ((а_n), (А_n)) є ряд ((–а_n), (–А_n)) (їх сумою є нульовий ряд).

Ці означення коректні, бо введені нові об'єкти дійсно є рядами, адже А_n + В_n= (а₁ + b₁) + ...+ (а_n + b_n), сА_n = ca₁ + ... + са_n3 –А_n = (-а₁) + ... + (-а_n).

Пропонуємо самостійно перевірити аксіоми лінійного простору. Важливим поняттям для рядів є їх сума та збіжність.

Означення. Сумою ряду (1) називається власне чи невласне число 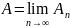, при умові, що ця границя існує. Якщо А R, то ряд (1) називається – збіжним, у протилежному випадку – розбіжним. Якщо ряд (1) має суму A, то пишемо

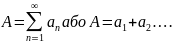
Таким чином, символ 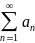вживається в двох сенсах: це позначення n–1 ряду або сума ряду. Така двозначність характерна для багатьох математичних символів, але вона не приводить до непорозуміння.

Згідно з означенням, розбіжний ряд може мати лише суми 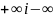, він може також не мати суми.

Якщо послідовність (а_n) фінітна і а_т - останній відмінний від нуля член, то A_k = А_т при k 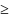m, отже . Це означає, що сума ряду є природним узагальненням суми скінченної послідовності чисел.

Теорема 1. Якщо ряд збіжний то послідовність його членів має границю 0.

Доведення. Оскільки a_n+1 = А_п+1 - А_п і , то

Теорема 1 виражає необхідну умову збіжності ряду.

Зауваження. Існують розбіжні ряди, загальні члени яких прямують до нуля.

При з'ясуванні збіжності ряду передусім перевіряємо, чи прямує до нуля загальний член. Із негативної відповіді випливає, що ряд розбіжний.

Теорема 2. Збіжні ряди утворюють підпростір лінійного простору всіх числових рядів.

Доведення. Нехай ряди ((a_n), (А_n)) і ((b_n), (В_n)) збіжні. Тоді lim(А_п + В_n) = lim А_n + lim В_n і lim сА_n = clim А_n , отже, збіжними є ((а_п + b_n), (А_n + В_n)) і ((са_n , сА_n)).

Наслідок. Якщо ряди 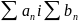, збіжні, то

Зауваження. Сума двох розбіжних рядів може бути як збіжним, так і

розбіжним рядом.

Теорема 3 (критерій збіжності Больцано - Коші).

Ряд збіжний тоді і тільки тоді, коли справедливее твердження

Доведення. Умову (3) можна переписати так:

Як відомо, умова (3') є необхідною і достатньою умовою збіжності послідовності (А_n) (див. теорему 1), отже, (3') є необхідною і достатньою умовою збіжності ряду (2).

Теорема 4. Нехай послідовність (а_n) монотонно спадна і ряд збіжний. Тоді

lim па_n = 0. (4)

Доведення. Твердження очевидне, якщо послідовність (а_n) фінітна. Нехай (а_n) відмінне від фінітної послідовності. Тоді а_n > 0 при всіх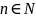 . Дійсно, в протилежному випадку внаслідок монотонності не виконувалася би необхідна умова збіжності ряду (теорема 1). Внаслідок теореми 3 справедливе твердження (3), де замість взято 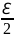. Нехай p> n = N і n + p = m. Користуючись умовою монотонності (а_n), можемо написати оцінку

яка справедлива при довільному m 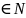, такому, що m >2N. Цим доведено рівність (4).

Означення. Нехай m 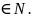Ряд

називається залишком (або залишком після т-го члена) ряду (2). Ряд (5) співпадає з рядом ((b_n), (В_n)), де b_n = а_т+n, В_n = А_т+n - A_m, .

Теорема 5. Ряд (5) збіжний тоді і тільки тоді, коли збіжний ряд (2). Якщо S і R_m - суми відповідно збіжних рядів (2) і (5), то справедливі рівності

R_m = S-A_m, (6)

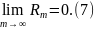
Доведення. Нехай (5) є позначенням ряду ((b_n), (В_n)). Тоді

Для збіжних рядів (2) і (5) маємо:

□

Зауваження. Перше твердження теореми 5 свідчить про те, що скінченна кількість членів ряду не впливає на його збіжність. Надалі ми часто будемо користуватися цим зауваженням, опускаючи члени ряду до деякого номера або замінюючи їх іншими членами.

Сума скінченної системи чисел має ту властивість, що нульові доданки можна не приймати до уваги. Цю властивість можна поширити також на ряди.

Введемо множину K = { : а_n ≠ 0}, яка може бути скінченною або нескінченною. Нехай K - скінченна множина. Тоді K можна впорядкувати за правилом зростання елементів згідно з наслідком теореми 3. 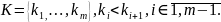Поряд з рядом (2) розглянемо суму a_k1 + ,..+ а_кт . Очевидно, послідовність частинних сум (А_n) ряду (2) є фінітною послідовністю, причому .

Якщо множина K нескінченна, то на підставі леми 2 існує строго зростаюча послідовність (k_n), така, що K={k_n: }. Очевидно, (а_kn) співпадає з підпослідовністю всіх відмінних від нуля членів послідовності (а_п). Покладаємо 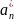= а_{кn ,} , і введемо ряд

Ряд (6) називається рядом відмінних від нуля членів ряду (2). Ряд (8) одержується із ряду (2) вилученням всіх нульових членів. Має місце

Теорема 6. Нехай ряд (2) має нескінченну кількість відмінних від нулячленів. Тоді ря ди (2) і (8) одночасн о збіжні чи розбіжні. Збіжні ряди (2) і (8) мають рівн і суми.

Доведення. Нехай (А_n) і (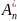 ) - послідовності частинних сум відповідно рядів (2) і (8). Легко довести, що A_kn = 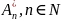. На підставі цих рівностей заключаємо: якщо ряд (2) збіжний, то

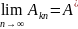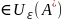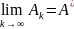Навпаки, якщо ряд (6) збігається до суми A^* , то . Нехай - довільне додатне число. Тоді існує таке N N, що A_kn при всіх n ≥ N. Якщо ціле число k задовольняє нерівності k_n < k < k_{n+1 ,} то а_к = 0, тому А_к = А_кn, отже, A_kn при всіх k ≥ k_N. Це означає, щo , тобто ряд (2) збіжний і має суму А*.

Теорема 5 дає можливість ототожнювати ряди (2) і (8). Тому надалі, при необхідності, будемо припускати, що члени ряду не приймають нульові значення.