Механизмы рассеяния Рассеяние на ионизированной примеси

Модель аналогична рассеянию Резерфорда. Пролетая в области заряженного центра, носитель будет отклоняться от исходного направления на угол, зависящий от скорости (чем выше скорость, тем меньше отклонение) и от прицельного расстояния (расстояние между направлением движения и рассеивающим центром). Строгая теория приводит к зависимости подвижности от температуры типа:

 

5.4

 

 

(С ростом температуры увеличивается скорость носителей!)

Экспериментально наблюдаемый показатель степени может несколько отличаться от 3/2.

к началу раздела  

Рассеяние на колебаниях решетки

Колебания решетки тоже являются нарушением идеальной периодичности и приводят к рассеянию.

Полный спектр колебаний решетки можно представить как набор гармонических колебаний. Простейший подход – колебания кристаллической решетки рассматривать как колебания струны. Каждый атом решетки находится на пересечении трех струн и участвует в колебаниях, которые существуют в этих струнах.

Если «струна» состоит из одинаковых атомов, находящихся в одинаковых положениях в элементарной ячейке, то в ней возможно существование длинноволновых колебаний (длина волны много больше расстояния между атомами). Если атомы разного сорта – то кроме длинноволновых колебаний возможно возникновение колебаний относительно некоторого центра масс в элементарной ячейке. В последнем случае частота колебаний гораздо выше и, соответственно, выше энергия одного колебания.

В первом случае говорят об акустических фононах – частоты соответствуют ультразвуковому диапазону. Во втором - об оптических фононах, частота соответствует области инфракрасного диапазона частот. (Фонон – по аналогии с фотоном, квазичастица, энергия которой равна ). В соответствии с законами квантовой механики энергия решетки квантуется и может поглощаться или испускаться только порциями – фононами. При относительно слабых энергиях носителей тока - электропроводность в слабых полях - носители могут передавать энергию решетке только дозами, равными энергии акустического фонона. При разогреве носителей в сильных полях возможно возникновение оптических фононов.

Рассеяние носителей на акустических фононах (просто – на колебаниях решетки) приводит к уменьшению их подвижности по закону:

5.5

Оба случая (рассеяние на ионизированных примесях и на колебаниях решетки) справедливы для невырожденного полупроводника. При наличии вырождения при низких температурах подвижность от температуры не зависит, а при высоких - обратно пропорциональна температуре.

 

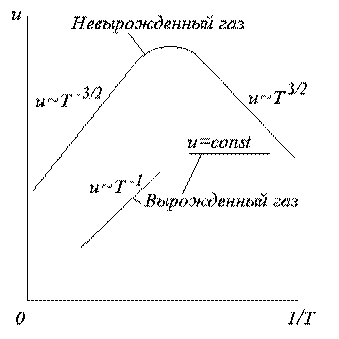
Рис.5.1. Температурная зависимость подвижности

( u – соответствует в наших обозначениях !)

 

В общем случае, все дефекты решетки влияют на подвижность носителей, но рассмотренные механизмы обычно влияют наиболее эффективно.

Практически всегда заранее можно сказать, какой механизм рассеяния преобладает в каждом конкретном случае. При низких температурах в легированных полупроводниках определяющим будет рассеяние на ионизированных примесях, при высоких – на колебаниях решетки.

к началу раздела