Введение

• Модель химической связи в полупроводниках

• Виды химической связи

• Основные понятия физики полупроводников.

• Типы носителей тока в полупроводниках.

• Другие характеристики носителей тока

• Концентрация свободных носителей тока

• Собственная проводимость.

• Примесная проводимость

• Электропроводность полупроводника

• Энергетическая диаграмма

• Энергия примесных центров

• Коэффициент диффузии носителей тока

• Соотношение Эйнштейна

• Время жизни неравновесных носителей тока

• Диффузионная длина неравновесных носителей тока

• Тест для самоконтроля

Модель химической связи в полупроводниках.

1. Полупроводниковыми свойствами обладают очень многие материалы с различными типами химической связи. Однако общим для всех этих материалов является наличие заметной доли ковалентной связи. Наиболее изученными и технологически освоенными являются полупроводниковые материалы на основе элементов IV группы таблицы Менделеева ( AIV ), соединений и твердых растворов на их основе элементов III и V групп и элементов II и VI групп.

Модель химической связи в этих материалах позволяет на единой основе объяснить поведение примесей в этих материалах и свойства самих материалов. Заметим, что полупроводник это, в общем, не материал, это состояние. Одно и то же соединение или материал в различных условиях могут проявлять различные свойства. Классический пример – углерод. В форме алмаза это полупроводник с очень интересными свойствами. Но существует еще большое количество различных форм углерода, свойства которых определяются характером химической связи. Большинство полупроводниковых соединений при плавлении переходят в металлическое состояние. Состояние, в котором находится материал, определяется минимумом энергии для конфигурации химических связей в условиях образования материала и/или в условиях изучения. (Так алмаз метастабилен в обычных условиях и медленно переходит в состояние графита – при комнатной температуре примерно за лет).

к началу раздела

Виды химической связи

 Существует 4 вида химической связи - Ван-дер-Ваальса, ионная, металлическая и ковалентная. Они различаются по силе связи, направленности и насыщенности. Сила связи - определяется работой разрыва. Направленность показывает, существует или нет выделенное направление в пространстве, в котором связь максимальна. Насыщенность - число частиц, которые одновременно взаимодействуют (любое или ограниченное).

Силы Ван-дер-Ваальса.

Связь между атомами инертных газов. Очень слабая. Критерий - величина тепловой энергии kT или энергии кванта света h n, достаточной для разрыва связи.

Модели сил Ван-дер- Ваальса

• поляризационная - атом - это система зарядов. При достаточно малом расстоянии между атомами центры положительных и отрицательных зарядов смещаются (в изолированном атоме они совпадают). Наведенные дипольные моменты приводят к появлению слабого взаимодействия.

• дисперсионная - атомы инертных газов имеют заполненные электронные оболочки в основном (невозбужденном) состоянии. Но конечная ширина уровней энергии приводят к возможности виртуальных переходов на возбужденные состояния. Время, в течение которого существует возбужденное состояние, мало, но не равно нулю. В возбужденном состоянии атомы обладают отличным от нуля дипольным моментом. Взаимодействие диполей и является причиной сил Ван-дер-Ваальса.

 

 

Ионная связь.

Коссель, при исследовании водных растворов, предложил теорию валентности, в соответствии с которой атомы элементов любой группы таблицы Менделеева стремятся иметь заполненную внешнюю электронную оболочку. Для этого они либо отдают лишние электроны другим атомам, либо отбирают у других атомов недостающие электроны. Заполненная полностью внешняя электронная оболочка соответствует электронной конфигурации инертных газов. После достижения своих целей они оказываются заряженными и, в связи с этим, за счет чисто кулоновского взаимодействия образуют химическое соединение. Модель Косселя совершенно справедлива для растворов, но несправедливо была распространена на все остальные случаи жизни, в том числе и на твердые тела. Различие между растворами и твердыми телами по отношению к теории валентности сводится к следующему. В водных растворах ионы находятся на относительно больших расстояниях из-за высокой диэлектрической проницаемости воды и быстро убывающие с расстоянием волновые функции электронов не перекрываются. В твердых телах появляется возможность перекрытия волновых функций, и проявляются более сильные взаимодействия. В частности, появляется возможность образования ковалентной и металлической связи. Перекрытие волновых функций приводит к значительному понижению энергии системы, а силы взаимодействия, как известно, связаны с производной энергии связи по расстоянию (с обратным знаком).

 к началу раздела

Металлическая связьобразуется из сферически симметричных s-состояний или при перекрытии волновых функций "почти свободных" (в пределах потенциального ящика) электронов.

Ковалентная связьобразуется при перекрытии волновых функций электронов в p-состояниях, которые имеют симметрию типа "гантели".

 

В квантовой механике энергия системы рассчитывается как :

,

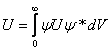где и волновые функции, описывающие состояние системы. Если взаимодействуют электроны двух соседних одинаковых атомов, причем набор четырех квантовых чисел у них одинаков, то этот интеграл оказывается весьма большим и положительным. Т.е. перекрытие волновых функций в этом случае приводит к большому повышению энергии системы, что с энергетической точки зрения не выгодно. Однако, если значения спинового квантового числа s для взаимодействующих электронов разное ( s может принимать только два значение +1/2 и -1/2), то, не изменяясь по абсолютной величине, интеграл меняет знак. Это приводит к сильному понижению энергии системы и появлению, соответственно, больших сил связи. (Сила это производная по координате от энергии с обратным знаком!). Это и есть ковалентная связь. Свойства ковалентной связи следуют из приведенной модели. Направленность объясняется типом симметрии перекрывшихся волновых функций, насыщенность следует из количества значений, которые принимает спиновое число – только 2), сила связи обусловлена величиной интеграла перекрытия. Примером материала с сильными ковалентными связями является алмаз.

Описанные выше модели могут реализовываться как в чистом виде, так и в различных комбинациях. Направленность связей (сила – вектор!), приводит к появлению разнообразных пространственных конфигураций кристаллических решеток.

И еще одно замечание. При образовании кристалла, атомы, входящие в его состав, в общем случае перестраивают свои электронные структуры. Внешние валентные электроны перестраиваются сильнее, электроны связанные сильнее с ядром – слабее. Перестройка может затрагивать не только величину энергии связи, но и изменять тип волновых функций валентных электронов. Примером может служить образование тетраэдрических связей.

Тетраэдрическая связь является характерной для полупроводниковых кристаллов, образованных из элементов 4-й группы таблицы Менделеева и для нескольких классов соединений. Свойства этих материалов и поведение в них элементов других групп таблицы Менделеева легко понять, если рассмотреть модель образования тетраэдрических связей.

 к началу раздела

Электронная конфигурация элементов IV группы таблицы Менделеева для графита, кремния и германия. Как известно s – состояние имеет сферически симметричную волновую функцию, p- состояние имеет симметрию типа симметричной гантели (или восьмерки). Т.е. волновые функции валентных электронов различны, а свойства связей в кристаллах этих материалов одинаковы для ближайших соседей. Причина такого противоречия лежит в сложном характере перестройки волновых функций валентных электронов при образовании кристалла.

В "нормальных" условиях (при температуре до 3000К, давление до 100ат.) для германия и кремния устойчивым будет кристалл, образованный следующим образом:

- один из s-электронов возбуждается и переходит в p-состояние -

- гибридизация одного s и трех p-состояний с образованием 4-х одинаковых состояний. Волновые функции этих состояний имеют симметрию типа асимметричной гантели.

Смысл гибридизации состоит в следующем. Волновые функции электронов есть решение дифференциального уравнения – уравнения Шредингера. Из теории дифференциальных уравнений известно, что если уравнение имеет два или несколько решений, то любая линейная комбинация этих решений будет так же решением этого дифференциального уравнения. Гибридизация волновых функций с точки зрения математики есть линейная комбинация волновых функций, а конкретный вид этой линейной комбинации определяется минимумом энергии системы в каждом конкретном случае. В результате с ионным остатком атома оказываются связанными 4 волновых функции по симметрии напоминающие восьмерки, у которых один лепесток значительно больше второго. Центры «восьмерок» находятся в центре ионного остатка.

к началу раздела

Квадрат модуля волновой функции есть плотность вероятности нахождения электрона и, следовательно, форма волновых функций связана с пространственным распределением заряда. Вся система напоминает четыре отрицательно заряженных шарика скрепленных в одной точке. Так как одноименно заряженные тела отталкиваются, минимум энергии системы будет тогда, когда большие "лепестки" волновых функций максимально удалены друг от друга, что соответствует ориентации лепестков по направлениям к вершинам тетраэдра, если ядро атома расположено в его центре.

В соответствии с принципом Паули, в одном состоянии, описываемом набором из 4-х квантовых чисел, может находиться только один электрон. Перекрытие волновых функций двух электронов, имеющих одинаковое значение спина, ведет к резкому повышению энергии системы (интеграл перекрытия большой и положительный). Если же спины противоположны по знаку, интеграл перекрытия меняет знак и энергия системы сильно понижается. Сила связи есть производная энергии связи по расстоянию (со знаком минус). Отсюда следует, что с перекрытием волновых функций связано существование достаточно сильной связи - ковалентной связи. И отсюда же следуют ее основные свойства - направленность (действует в направлении "оси лепестка волновой функции"), насыщенность (спин имеет только 2 значения - s = ±1/2).

При образовании кристалла минимум энергии системы будет достигаться при образовании ковалентной связи каждым из валентных электронов (находящимся в sp 3 гибридизированном состоянии). В связи с этим атомы элементов IV группы при образовании кристалла устанавливают тетрагональные связи - для каждого атома (центр тетраэдра) имеется 4 соседа, расположенных в вершинах этого тетраэдра.

Атомы примесей в кристалле типа АIV - могут находиться в различных состояниях. Наиболее удобно (т.е. с меньшим повышением энергии системы) для атомов III и V групп таблицы Менделеева будет привести свою электронную конфигурацию в состояние, близкое к электронной конфигурации основных атомов кристалла. Для элементов V группы (мышьяк, сурьма, фосфор) электронная конфигурация имеет вид . По сравнению с электронной конфигурацией элементов IV группы, они имеют один лишний p-электрон. Поэтому им удобно отдать его (зарядившись до + e) и затем проделать те же манипуляции с остальными электронами, что и основные атомы кристалла. "Лишний" электрон при этом оказывается просто слабо связанным со своим ионом (за счет высокой диэлектрической проницаемости кристалла) и

легко переходит в свободное состояние, т.е. в зону проводимости. Таким образом, элементы V группы являются эффективными донорами кристаллах типа АIV .

к началу раздела

Элементы III группы (бор, индий, галлий, алюминий) имеют электронную конфигурацию 1, т. е. до электронной конфигурации элементов IV группы им не хватает одного электрона. Естественно, им удобно захватить недостающий электрон (зарядившись до - e) и повторить все остальные манипуляции до образования sp 3-гибридизированных связей. Т.е. атомы этих элементов будут эффективными акцепторами в полупроводниках типа АIV.

Атомам II и VI групп еще сложней перестроить свои оболочки. Их электронные конфигурации и , соответственно. Их электрическая активность имеет более сложный характер - они образуют несколько многозарядных центров в запрещенной зоне и типы и количество этих центров определить не так просто.

Трудности, связанные с перестройкой электронных оболочек, затрудняют вхождение этих примесей в кристалл. Существует вполне четкая корреляция между электронной конфигурацией атомов и растворимостью их в кристалле. Чем сильнее отличается электронная конфигурация, тем меньше растворимость. Так, в кристаллах AIV элементы IV группы таблицы Менделеева растворяются в любых пропорциях. Элементы III и V групп имеют ограниченную растворимость - предельная растворимость порядка сотых - тысячных долей процента. Элементы II и VI групп имеют еще на три порядка меньшую растворимость. Растворимость меди, платины и переходных элементов в кремнии на уровне .

Коэффициенты диффузии также зависят от различия в электронных структурах. Чем ближе электронная структура, тем медленнее диффундируют атомы в кристалле. Минимальный коэффициент диффузии атомов основного вещества и элементов IV группы. На порядка больше коэффициенты диффузии атомов III и V групп. Элементы типа меди в кремнии имеют коэффициент диффузии в твердом кремнии близкий по порядку величины к коэффициентам диффузии в жидкостях. Следует отметить, что и растворимость и коэффициенты диффузии зависят еще и от других факторов - размеров атомов, сродства к электрону и т.д. Поэтому можно говорить только о корреляции растворимости и коэффициентов диффузии со структурой электронных оболочек.

к началу раздела

Рассмотрим теперь процесс образования кристаллов типа AIIIBV – соединений элементов третьей и пятой групп таблицы Менделеева. Это типичные полупроводниковые материалы антимониды, фосфиды и арсениды индия, галлия и алюминия.

Электронная конфигурация валентных электронов элементов третьей группы имеет вид . Электронная конфигурация элементов пятой группы, соответственно, . На первом этапе один из p – электронов элемента пятой группы переходит к элементу третьей группы, при этом образуются два иона, у которых электронные оболочки похожи на электронную оболочку элемента четвертой группы, но имеют нескомпенсированные заряды. Далее они проделывают те же манипуляции, что и элементы четвертой группы, т.е. один из s – электронов возбуждается до p – состояния, затем происходит гибридизация s – и p – оболочек и в результате каждый из атомов имеет по четыре одинаковых валентных волновых функций, с единственным отличием – наличие нескомпенсированных зарядов. Атомы третьей группы заряжены отрицательно, атомы пятой группы – положительно. В отличие от кристаллов AIV перекрытие волновых функций соседних атомов оказывается несколько несимметричным. Центры положительных и отрицательных зарядов не совпадают, такая система имеет отличный от нуля дипольный момент, а сама связь оказывается не чисто ковалентной, а с некоторой долей ионной составляющей.

Примесные атомы элементов из групп ближайших соседей как и в предыдущем случае ведут себя понятным образом. Элементы VI группы имеющие электронную конфигурацию охотно теряют один p-электрон (отдают его в общее пользование) и могут занять место в кристаллической решетке элемента пятой группы, т.е. ведут себя как доноры. Элементы II группы акцептируют (захватывают) соседский электрон, получают при этом возможность занять место элемента III группы, при этом рядом с ними оказывается недостаток одного электрона, структура, которая ведет себя как положительно заряженная подвижная частица – «дырка». Таким образом, элементы шестой группы ведут себя как доноры – каждый атом вносит в систему один свободный (точнее слабо с ним связанный) электрон, который легко отрывается и участвует в проводимости. Элемент второй группы приносит с собой слабо связанную дырку, которая легко отрывается и также участвует в переносе заряда в полупроводнике. Несколько сложнее в кристаллах AIIIBV ведут себя элементы четвертой группы таблицы Менделеева. Они могут занять место как элемента пятой группы, и тогда они будут акцепторами, так как у них не будет хватать одного электрона. Но могут сесть на место элемента третьей группы, тогда у них на внешней оболочке будет один лишний электрон, т.е. они будут проявлять свойства донора. Куда на самом деле будут попадать атомы элементов IV группы, зависит от условий роста слоя, в котором они будут находиться. И опять, все будет определяться минимумом энергии системы и, в общем случае, скоростью движения фронта кристаллизации. Условиями роста можно управлять, поэтому элементы IV группы могут быть использованы для создания областей и с электронным и с дырочным типом проводимости.

В заключение отметим, что поведение примесей в кристаллах различного типа носит общий характер – доноры для германия, будут донорами и для кремния и для алмаза, а электрическая активность элемента VI группы будет иметь один и тот же тип для всех соединений типа AIIIBV и твердых растворов на их основе. Правда, некоторые особенности все-таки проявляются, энергия связи, растворимость, коэффициенты диффузии и т.п. будут различаться.

к началу раздела

Основные понятия физики полупроводников.

Для того чтобы понимать в дальнейшем, о чем идет речь, есть смысл познакомиться с кратким обзором основных понятий, которыми оперирует физика полупроводников. Познакомиться с основными терминами и наглядными моделями, иллюстрирующими смысл этих терминов. Заметим, что при появлении в тексте следующих разделов новых понятий или терминов, можно воспользоваться пояснениями в правой колонке текста, но для общего представления есть смысл внимательно прочесть этот раздел.

Еще одно замечание. Можно было бы о многих вещах, относящихся к курсу общей физики, не упоминать, считая, что все, кому доведется пользоваться этим пособием, все о них прекрасно знают, но многолетний опыт…. Поэтому кое-что придется напоминать.

Полупроводники отличаются от всех прочих материалов целым букетом свойств, и в этом их основное достоинство.  

к началу раздела

Типы носителей тока в полупроводниках.

Начнем с частиц, которые могут переносить заряд в полупроводниках. В металлах ток переносится одним типом носителей – электронами. В полупроводниках вводится еще один тип носителей – дырки. Хотя на самом деле ток все-таки переносится, конечно, электронами и дырки это просто удобный образ. Когда в бокале шампанского всплывают пузырьки газа, мы говорим о том, что всплывают именно пузырьки газа. Но, с другой стороны, то же явление можно описывать как движение все остальной части системы – жидкость опускается. Так же и с движением электронов в полупроводнике. Каждый электрон при движении переносит заряд так сказать индивидуально. Но если один из атомов, сидящих в узле кристаллической решетки полупроводника, потерял один из своих электронов, которые обычно с ним связаны, то в этом месте окажется избыточный положительный заряд. На первый взгляд этот заряд неподвижен и не может рассматриваться как носитель тока. Но от ближайшего соседа на это место ЛЕГКО может перейти другой электрон. Для этого перехода не требуется большой энергии от внешних источников, при комнатной температуре переход оказывается почти безбарьерным. А при этом положительный заряд, по абсолютной величине равный заряду электрона, перейдет в направлении, противоположном перемещению электрона. При отсутствии внешнего электрического поля это пустое положительно заряженное место будет хаотически блуждать по кристаллу. Но если напряженность электрического поля отлична от нуля, то движение дырки станет вполне направленным, причем направленным в сторону, противоположную направлению движения электронов, но ток, связанный с движением дырок будет иметь то же направление. И возникает дилемма – рассматривать процесс перемещения этих «свободных мест» как коллективное движение всех валентных электронов в кристалле, или ввести несколько необычное понятие «дырки» и следить за ними отдельно. Интересно, что если принять за основу понятие дырки то перенос единичного заряда будет связан с движением одной единственной частицы. Если же рассматривать процесс как коллективное движение электронов, то субъект движения все время меняется. Правда, в квантовой механике электроны неразличимы! Обратите внимание на тот факт, что перемещение дырки связано не с движением всех остальных свободных электронов, а с перемещением связанных, валентных, электронов, которые не могут перемещаться, если рядом нет свободного места. Удобным оказалось ввести понятие дырки как переносчика заряда, или носителя тока. При этом ей пришлось приписать набор свойств, необходимых для описания носителя тока, полностью аналогичный набору свойств электрона проводимости, правда, значения этих свойств оказались отличными от свойств электрона.

к началу раздела

Другие характеристики носителей тока

Поведение носителей тока в полупроводниках настолько разнообразно, что для его описания есть смысл ввести еще несколько определений, иначе не будет понятно, о чем идет речь.

• основные и неосновные носители тока. Если полупроводник имеет четко выраженный тип проводимости, например электронов в нем гораздо больше, чем дырок, то электроны логично называть основными носителями. Но одновременно приходится следить за поведением тех носителей, которых меньше, чем основных. Эти носители называются соответственно, неосновными. Причем поведение неосновных носителей зачастую оказывается более интересным, чем основных.

• равновесные и неравновесные носители тока. При отсутствии внешних воздействий в однородном полупроводнике устанавливаются равновесные концентрации носителей тока. Если есть неоднородности в уровне легирования, или в полупроводнике действует отличное от нуля электрическое поле, или полупроводник освещается светом с энергией кванта превышающей ширину запрещенной зоны, то термодинамическое равновесие нарушается, и концентрации носителей могут отличаться и значительно от равновесных значений. Да и свойства носителей могут отличаться от свойств равновесных носителей. Поэтому есть смысл различать неравновесные и равновесные носители тока.

к началу раздела

Концентрация свободных носителей тока  

В металлах концентрация свободных носителей тока настолько постоянна, что о ней не принято особенно говорить. В полупроводниках это один из важнейших параметров, от которого зависят свойства материала и приборов из него изготовленных.

В полупроводниках кроме двух типов носителей тока принято различать еще два вида проводимости – собственную и примесную.

к началу раздела

 Собственная проводимость.

Это понятие можно представить себе следующим образом. Пусть есть идеальный чистый кристалл полупроводника. Примесей нет. Его проводимость определяется числом валентных электронов, которые за счет энергии теплового движения оторвались от своих атомов и теперь могут двигаться по кристаллу. В результате атомы кристаллической решетки потеряли часть валентных, связанных с ними электронов. То есть появилось равное количеству свободных электронов количество свободных дырок. Это есть «собственные» носители тока и проводимость, сними связанная, называется собственной проводимостью.

Примесная проводимость

Если в идеальной решетки полупроводникового кристалла появился атом, у которого число валентных электронов отличается на единицу от числа валентных электронов основных атомов кристалла, то, при встраивании этого атома в кристаллическую решетку, ему выгодно выровнять число валентных электронов с окружающими атомами. Если у него был лишний электрон, то он оказывается слабо связанным и легко переходит в свободное состояние. При комнатной температуре он почти всегда свободен. Примесь такого типа является донором свободных электронов и, соответственно, называется донором. Если у атома было меньше валентных электронов чем у соседей, то он свяжет («акцептирует») свободный электрон или один из электронов, связанных с соседними атомами. При этом в первом случае исчезнет один из свободных электронов, а во втором – появится свободная дырка. Такие атомы называются акцепторами

Появление носителей, связанных с попаданием примесей в кристалл, называется примесной проводимостью. Когда говорят о том, что полупроводник собственный, имеют в виду, что собственных носителей, связанных с ионизацией решетки, много больше, чем примесных носителей, чье появление связано с ионизацией примесных центров.

Следует отметить, что любой примесный центр может обладать донорными и/или акцепторными свойствами, т.е. быть причиной появления (или исчезновения – компенсации) свободных электронов или дырок. Но есть смысл различать эффективные доноры и эффективные акцепторы с одной стороны, и примеси с относительно глубокими энергетическими уровнями, которые при комнатной температуре могут остаться не ионизованными. На каждый атом эффективного донора, введенного в кристалл, появляется при комнатной температуре один свободный электрон, на каждый атом акцептора в чистом кристалле появляется свободная дырка. Дырка и свободный электрон при встрече могут исчезнуть из числа свободных носителей, т.е. прорекомбинировать.

Эта корреляция концентрации свободных носителей и концентрации эффективных доноров и эффективных акцепторов одно из замечательных свойств полупроводника. Ни один другой тип материала таким свойством не обладает. Из этой корреляции следует необходимость предельно глубокой очистки полупроводниковых материалов от неконтролируемых примесей и необходимость точной регулировки концентрации примесей, вводимых в полупроводник при выращивании кристаллов или эпитаксиальных слоев или при создании полупроводниковых приборов и/или интегральных схем.

Отметим еще, что обычно в литературе определение «эффективный» обычно только подразумевается, а все прочие примеси объединены понятием примесных центров с глубокими уровнями, имеется в виду большая энергия ионизации этих примесных центров по сравнению с энергией теплового движения – kT.

к началу раздела

Электропроводность полупроводника

 Если в некотором пространстве существует направленный поток заряженных частиц, движущихся в одном направлении, то плотность тока, связанного с этими частицами может быть рассчитана из соотношения

,

1.1

где e-заряд электрона, n – концентрация электронов, V – скорость электронов.

Если направленная скорость движения электронов в полупроводнике вызвана внешним и не очень большим электрическим полем, то величина скорости оказывается пропорциональной напряженности поля:

1.2

и, следовательно, ток будет пропорционален напряженности электрического поля:

,

1.3

здесь коэффициент пропорциональности между скоростью электронов и напряженностью поля – это подвижность носителей тока, ли скорость в поле с единичной напряженностью. Индекс nпоказывает, что это подвижность электронов.

С учетом того факта, что в полупроводниках два типа носителей тока это выражение следует переписать в виде:

1.4

где появились концентрация дырок p и, соответственно, подвижность дырок - .

Если теперь вспомнить закон Ома в дифференциальной форме, связывающий плотность тока и напряженность поля:

,

1.5

то можно ввести понятие электропроводности полупроводника:

1.6

где первое слагаемое в скобках описывает электропроводность, связанную с электронами, второе – с дырками.

к началу раздела

Энергетическая диаграмма

Когда мы говорили о собственной проводимости, проводимость, связанная с дырками, объяснялась перемещением электронов от валентной связи с одним атомом к другому атому, или перемещением дырок по валентным связям атомов. Если всю совокупность валентных электронов и интервал энергий, которые они могут принимать, рассматривать как некоторую валентную зону, в основном заполненную электронами. Перемещение электронов в этой зоне возможно только при наличии свободного места – дырки.

Для отрыва валентного электрона и перевода его в свободной состояние необходимо затратить некоторое количество энергии, равное энергии связи валентного электрона со своим атомом. Если подведенной извне энергии не хватит – электрон останется связанным, если хватит – станет свободным. Все свободные электроны можно считать находящимися в другой зоне – в зоне проводимости. При этом минимальная энергия, которой будет обладать электрон в свободном состоянии («дно зоны проводимости»), будет отстоять от максимальной энергии, которой он обладал в связанном состоянии («потолок валентной зоны») на величину энергии, которую в чистом идеальном кристалле электроны не могут иметь. Этот диапазон энергии естественно назвать запрещенной зоной энергии.

к началу раздела

Энергия примесных центров

Если в кристалле появился примесный центр, у которого есть слабо связанный электрон (эффективный донор), то для перевода этого электрона в свободное состояние (в зону проводимости) необходима небольшая, но отличная от нуля энергия. Естественно приписать этому атому некоторое состояние в запрещенной зоне, энергетический уровень которого будет отстоять от дна зоны проводимости на величину энергии связи. Т.е. при сообщении этому электрону энергии, равной зазору между положением его в запрещенной зоне и дном зоны проводимости, электрон перейдет в зону проводимости.

Совершенно аналогично, акцепторные уровни в запрещенной зоне следует поместить на расстоянии равном энергии перехода из валентной зоны на уровень акцептора от потолка валентной зоны.

Таким образом, в реальном кристалле запрещенная зона не совсем запрещена - в ней находятся уровни энергии различных примесных центров и других точечных дефетков – вакансий, межузельных атомов и т.п.

к началу раздела

Коэффициент диффузии носителей тока

В отличие от металлов, концентрация носителей тока в полупроводниках может меняться от точки к точке. Это приводит к тому, что в полупроводниковом кристалле в определенных условиях (но часто!) могут появляться отличные от нуля градиенты концентраций носителей тока. Неравномерность распределения частиц в пространстве всегда приводит появлению диффузионных потоков. Поскольку носители тока в полупроводниках заряжены, то связанный с ними диффузионный поток на самом деле есть электрический ток, только в отличие от токов в металлах он не связан с напряженностью поля, он связан с неравномерностью распределения носителей именно в пространстве. Надо сказать, что такой диффузионный тока на самом деле существует не только в полупроводниках, он существует везде, кроме металлов. Но в полупроводниках его роль особенно важна – диффузия носителей является основой работы большинства полупроводниковых приборов. В соответствии с первым законом Фика, диффузионный поток всегда пропорционален градиенту концентрации:

1.7

Здесь D – коэффициент диффузии, который зависит от легкости перемещения частиц в пространстве. Знак минус показывает, что направление потока противоположно направлению градиента, который направлен в сторону возрастания концентрации диффундирующих частиц.

В случае существования градиента концентрации носителей тока, с диффузионным потоком носителей должен быть связан перенос зарядов, и, следовательно, некоторый диффузионный ток. Для положительно заряженных дырок направление тока и потока совпадают, т.е. диффузионный ток дырок следует записывать в виде:

1.8

Здесь появление индекса у коэффициента диффузии означает, что речь идет о коэффициенте диффузии дырок.

Для отрицательно заряженных электронов направление тока будет противоположно направлению потока:

.

1.9

к началу раздела

Соотношение Эйнштейна  

Обратите внимание, что у нас появилось два понятия, связанные с одним и тем же свойством носителей тока. Действительно, ранее введенная подвижность носителей тока и введенный в предыдущем параграфе коэффициент связаны с легкостью движения носителей в решетке кристалла. С аналогичной ситуацией впервые столкнулся Альберт Эйнштейн при исследовании электропроводности (ионной) щелочногаллоидных кристаллов. При этом он получил соотношение между подвижностью и коэффициентом диффузии для ионов, которое оказывается справедливым и для не очень сильно легированных полупроводников, которое известно под названием соотношения Эйнштейна:

1.10

Естественно, что соотношение справедливо отдельно для электронов, отдельно для дырок. Таким образом, если известна подвижность носителей тока какого-либо сорта, то всегда можно посчитать соответствующий коэффициент диффузии.

к началу раздела

Время жизни неравновесных носителей тока

В полупроводнике относительно легко можно получить неравновесную концентрацию носителей тока за счет подводе энергии от внешнего источника. Например, при освещении полупроводника светом с энергией квантов , где - ширина запрещенной зоны, электроны могут перейти из валентной в зону проводимости. Пока освещение действует, концентрация свободных электронов (и дырок в силу нейтральности полупроводника) будет превышать равновесную. Естественно, что при выключении источника света система со временем должна вернуться к состоянию равновесия. Но в принципе процесс перехода к равновесию может протекать с различным темпом. Характеристикой темпа возвращения к равновесию будет так называемое время жизни неравновесных носителей тока. В связи с тем, что нас интересует поведение большого по численности ансамбля частиц, нет смысла следить за поведением каждой частицы, нужно иметь дело со средними величинами. Удобно в этом случае ввести параметр, который будет описывать снижение неравновесности системы. В нашем случае нарушение равновесия связано с лишними частицами и таким параметром будет время, в течение которого концентрация неравновесных частиц уменьшится в e – раз. Если отклонение от равновесной концентрации не очень велико, т. е. концентрация неравновесных носителей много меньше концентрации равновесных, зависимость концентрации неравновесных носителей от времени будет описываться выражением:

,

1.11

где – время, в течение которого неравновесная концентрация уменьшится в е раз. Действительно, если , то .

к началу раздела

Диффузионная длина неравновесных носителей тока

 Если поверхность полупроводника освещать светом с большой ( ) энергией квантов и, что связано с этим, с большим коэффициентом поглощения, то неравновесные носители будут возникать в основном в области, где поглощается основная часть квантов. При этом возникнет неоднородное распределение неравновесных носителей тока, и связанный с этой неоднородностью диффузионный поток от поверхности в объем полупроводника. Поскольку при диффузии концентрация носителей будет еще убывать за счет рекомбинации в связи с конечным временем жизни, то распределение носителей по глубине в стационарных (установившихся) условиях будет описываться выражением:

,

1.12

где - так называемая диффузионная длина неравновесных носителей тока. Очевидно, что диффузионная длина должна быть связана с коэффициентом диффузии и временем жизни неравновесных носителей тока:

1.13

Очевидно, что электроны и дырки могут иметь различные значения и коэффициентов диффузии и времени жизни и диффузионной длины. Обычно это обозначается соответствующим индексом n или p.

к началу раздела

Понятие энергетического спектра.

Для описания электрофизических свойств любого материала полезно знать, как распределены носители тока по энергии, т.е. какой вид имеет энергетический спектр – сплошной, полосатый или дискретный. На основе энергетического спектра обычно производится разделение материалов на металлы, полупроводники и диэлектрики. Правда однозначной классификации при этом не получается, но об этом чуть позже.

Об энергетическом спектре.

С чем связаны различия в энергетических спектрах.

В классической физике все значения энергии разрешены, и это интуитивно считается нормальным. Системы, состоящие из электронов, ионов и т.п. описываются квантовой механикой, и здесь ситуация несколько иная.

Свободная частица может принимать любые значения энергии. В дальнейшем нам будет полезно вспомнить, как связана кинетическая энергия частицы с ее импульсом:

2.1

Это так называемое дисперсионное соотношение, которое оказывается более сложным для других систем и, тем не менее, весьма полезным.

Нам надо только договориться, что считать свободной частицей. Здесь придется воспользоваться одним из фундаментальных положений квантовой механики – принципом неопределенности Гейзенберга. В соответствии с этим принципом «неопределенности» координат и «неопределенности» импульсов должны удовлетворять соотношению:

2. 2

Отсюда и следует понятие «свободы» частицы – если она может находиться в любой точке пространства – она свободна и неопределенность ее координат равна бесконечности. Любые ограничения ее «свободы» приводят к конечным значениям «неопределенности» ее координат, и следовательно к неопределенности величин компонентов импульса и даже к неопределенности самого понятия «импульса». Следовательно, и с энергией начинаются проблемы. Какие-то значения энергии оказываются разрешенными, какие-то запрещенными. Т.е. возникает некоторый энергетический спектр, связанный с ограничениями для движения частиц. Так кулоновское взаимодействие электрона с ядром приводит к возникновению «дискретного энергетического спектра».

Интересно, что вид энергетического спектра зависит от размерности пространства, в котором может перемещаться электрон, и это приводит к так называемому «размерному квантованию» энергии, что является одним из основных понятий наноэлектроники. Как будет показано далее, периодический потенциал, связанный с заряженными ионами, приводит к «полосатому» энергетическому спектру. И, кроме того, дисперсионное соотношение для каждой разрешенной полосы будет отличаться от соотношения ( 2.1).

к началу раздела  

Строго говоря, информация о зонной структуре может быть получена на основе решения уравнения Шредингера для системы частиц, в которую входят все электроны и все ядра. Соответственно, в это уравнение войдет число переменных (координат) в три раза большее, чем общее число частиц в системе. Или для каждой из этих частиц надо написать свое уравнение и решать все эти уравнения совместно. В результате получается система, состоящая для кристалла объемом 1 более чем из уравнений, для решения которой используют достаточно грубые приближения. Естественно при этом решение получается не очень строгим и не очень похожим на истину.

Из решения уравнения Шредингера в принципе может быть получена информация о разрешенных значениях энергии – область разрешенных значений оператора энергии E, т.е. значения оператора энергии, для которых существуют решения дифференциального уравнения Шредингера. И зависимость энергии от импульса для этих разрешенных значений энергии, т.е. соответствующие каждой полосе разрешенных энергий дисперсионные соотношения типа ( 1.1). Полученный таким образом набор информации в виде графиков зависимостей называется зонной или энергетической диаграммой для соответствующего материала. Естественно, что из анализа столь сложной системы и выполненного при достаточно грубых допущениях получается только самая общая картина для зонной диаграммы. В дальнейшем для каждого полупроводникового материала реальная зонная диаграмма уточняется путем обобщения результатов многочисленных экспериментов.

В связи с тем, что зонная диаграмма очень важна для понимания всех свойств полупроводникового материала, есть смысл рассмотреть эту проблему на качественном уровне несколько с другой стороны.

к началу раздела

Качественная модель энергетического спектра

Если исходить из того, что в кристалл – это просто объединение атомов, каждый из которых имеет определенный набор разрешенных энергетических уровней, а остальные значения энергии запрещены (в терминах физики полупроводников – плотность состояний отлична от нуля только для разрешенных уровней энергии, для остальных - равна нулю), то на качественном уровне можно попытаться представить себе, что будет происходить с разрешенными уровнями энергии при сближении атомов и образовании из них кристалла.

Следует отметить, что уровни энергии электронов в атоме могут быть вырождены – т.е. одному значению энергии может соответствовать несколько состояний. Из курса общей физики известно, что при внешнем воздействии вырождение может быть снято – уровень расщепляется на несколько близко расположенных подуровней.

Когда сближаются два атома, энергетические уровни их электронов не могут оставаться неизменными. Это запрещено еще одним фундаментальным принципом квантовой механики – принципом Паули, согласно которому в одном состоянии не может существовать более одной частицы с одинаковым набором 4-х квантовых чисел. В связи с этим каждый уровень расщепляется на два (или более, если исходные уровни вырождены), причем разность энергии будет зависеть от степени сближения атомов (расстояния между атомами) и от энергии электронного уровня в атоме. Поэтому внешние (валентные), относительно слабо связанные электроны, меняют свою энергию сильнее, чем электроны на внутренних, более глубоких уровнях.

Изменение электронной конфигурации

На самом деле процесс объединения атомов при образовании кристалла оказывается более сложным, чем описано выше. В большинстве случаев происходит перестройка конфигурации внешних (валентных) электронов. Для элементов четвертой группы таблицы Менделеева (АIV) – углерода, кремния и германия электронная конфигурация имеет вид – . При образовании кристалла электронная конфигурация существенно изменяется. Схема этих изменений может быть представлена следующим образом:

на первой стадии происходит возбуждение системы – один из электронов переходит из s - состояния в p -состояние. Электронная конфигурация при этом выглядит как ( n ) . Затем происходит так называемая гибридизация волновых функций этих электронов. Так как волновые функции s – и p - состояний есть решения дифференциального уравнения Шредингера, то любая линейная комбинация волновых функций тоже является решением уравнения Шредингера. А какая именно комбинация реализуется при этом, определяется минимумом энергии системы. В результате образуется 4 одинаковых по симметрии волновых функций и, как следствие, все валентные электроны имеют одинаковые волновые функции типа гибрид .

При построении кристалла объединяется сразу очень большое число атомов. При этом возникают зоны разрешенных и запрещенных значений энергии. Каждому разрешенному уровню энергии в каждом из атомов в образовавшейся разрешенной зоне будет соответствовать, по крайней мере, один подуровень. Если для оценки принять ширину разрешенной зоны энергий для внешних валентных электронов за 1 эВ, то средний зазор между подуровнями энергии в разрешенных зонах, оказывается, по порядку величины равным эВ. Много это или мало можно понять из сравнения с энергией теплового движения частиц при комнатной температуре – кТ . При комнатной температуре ( T=300K) эта энергия равна 0.026 эВ. Поэтому электрон не сможет почувствовать зазора между подуровнями энергии, для него «пространство энергий» внутри разрешенной зоны будет непрерывным. Однако дискретность подуровней все-таки необходимо учитывать – она сказывается на неравномерности распределения подуровней по ширине разрешенной зоны энергий, т.е в непостоянстве плотности состояний при изменении энергии в пределах разрешенной зоны. Зависимость плотности состояний от энергии для разрешенных зон мы рассчитаем позже.

Естественно, что областям энергии, для которых плотность состояний в атоме была равна нулю, в кристалле тоже будут соответствовать области, для которых плотность состояний равна нулю. Обратите внимание – эти энергии не равны, они просто соответствуют друг другу. Все энергетические уровни электронов в атоме не только расщепляются при образовании кристалла, но и сдвигаются за счет сильного взаимодействия с соседними атомами. Т.е. между полосами с разрешенными значениями энергии могут находиться области с запрещенными значениями. Это так называемые «запрещенные зоны» энергий. Существование запрещенных зон энергий не должно вызывать удивления. Во-первых, этим областям в атомах тоже соответствовали запрещенные интервалы энергии. Во-вторых, смысл этих запретов достаточно прозрачен. В атоме, чтобы перевести электрон с одного уровня энергии на другой (ближайший!), необходимо затратить энергию равную разности энергии между уровнями. Нельзя «частично» оторвать электрон от уровня, только полностью. Для кристалла еще более наглядно – для отрыва валентного электрона от атома решетки нужно затратить энергию равную ( или большую!) ширине запрещенной зоны.

Таким образом, при образовании кристалла возникает система разрешенных и запрещенных зон, от структуры и степени заполнения состояний электронами зависят его основные физические свойства. Так, если последняя заполненная зона заполнена частично, или последняя заполненная зона перекрылась со следующей пустой, то кристалл будет проявлять металлические свойства. Если последняя заполненная зона полностью заполнена, а следующая пустая (соответствующая возбужденным состояниям электрона в атоме!), то, в зависимости от ширины запрещенной зоны между ними кристалл будет проявлять полупроводниковые или диэлектрические свойства. Если ширина запрещенной зоны не очень велика, то существует заметная вероятность теплового возбуждения электрона из полностью заполненной (валентной) зоны в полностью пустую (зону проводимости).

Если последняя заполненная зона полностью заполнена электронами, а следующая пустая зона расположена на большом расстоянии от нее, то проводимость кристалла отсутствует. Понять это можно достаточно легко, если вспомнить, что в валентной полностью заполненной зоне находятся электроны, привязанные к соответствующим атомам кристаллической решетки, т.е. они не свободны, и перемещаться по кристаллу не могут. Правда, если рядом есть атом, потерявший по каким-то причинам один из своих валентных электронов, то переход связанного электрона от полностью заполненного атома к частично заполненному не приведет к заметному изменению энергии системы. При этом «пустое место» передвинется в противоположном направлении. В результате заряд будет переноситься по кристаллу. Можно рассматривать перенос заряда как коллективный процесс, при котором большое количество электронов переместились, причем каждый из них переместился на одно межатомное расстояние. А можно считать, что перемещается «пустое место» (дырка), но перемещается, как полагается некой «квазичастице», как нечто целостное и переносит при этом заряд, равный по абсолютной величине заряду электрона, но, поскольку дырка движется в противоположном направлении, ей придется приписать положительный заряд. Эта ситуация очень похожа на поведение пузырьков газа в бокале шампанского – одни видят всплывающие пузырьки газа, другие видят, как опускается вся жидкость, понижается ее центр тяжести. Надо отметить, что оба описания процесса эквивалентны и отличаются только уровнем наглядности. Проводимость, связанная с движением дырок, хотя на самом деле все-таки двигаются электроны, отличается по некоторым параметрам от привычной электронной проводимости. Это естественно, поскольку коллективное движение электронов происходит несколько иначе, чем непосредственный процесс переноса заряда одним электроном. Поэтому приходится вводить два типа носителей, которые отличаются по величине подвижности (у электронов она обычно значительно выше). Каждой из этих квазичастиц приходится приписывать свойство, которое обычно называют массой, но которая таковой не является. В кристалле и электроны и дырки описываются так называемой « эффективной массой», которая измеряется в единицах массы свободного электрона, но может быть значительно меньшей или большей, чем масса свободного электрона. Величины эффективных масс непосредственно связаны с энергетической диаграммой.

Качественная картина энергетической диаграммы на самом деле не полностью отражает существо дела. Более строгий (правда менее наглядный) подход, связанный с анализом системы уравнений Шредингера для кристалла, позволяет получить больше информации о структуре энергетических зон. Подробнее этого мы коснемся далее, а здесь, для наглядности, мы рассмотрим первый из обещанных апплетов, который показывает, как выглядит структура энергетических зон для кремния ( Si) , германия ( Ge) и их твердых растворов ( Si x Ge 1- x).

Замечание Расположите на экране два окна, одно с соответствующими пояснениями, в другом откройте апплет. Для удобства работы расположите окна так, чтобы они не перекрывались

Некоторые пояснения к апплету. Для чистых германия и кремния валентная зона состоит из трех подзон или долин. Это связано со снятием вырождения уровней валентных электронов в атоме при образовании кристалла. На самом деле энергия зависит от импульса электронов, что и показано на диаграмме. В этом нет ничего удивительного. Энергия любого камня зависит от импульса: . Другое дело, что в кристалле понятие импульса теряет смысл, приходится вводить понятие квазиимпульса, т.е. нечто похожего на импульс, но свойства квазиимпульса сильно отличаются от обычного импульса.

В валентной зоне зависимость энергии от импульса не однозначна – мы видим три кривых, отличающихся друг от друга по кривизне в точке максимумов.

Поскольку эффективная масса дырки связана с формой зависимости энергии от квазиимпульса, то приходится признать, что в валентной зоне существует несколько сортов дырок, отличающихся по массе - есть легкие и тяжелые дырки. Еще более сложная картина в зоне проводимости. Там тоже три долины, но одна имеет минимум в точке, где квазиимпульс равен нулю, а две других в точках, где квазиимпульс отличен от нуля. Как будет видно в дальнейшем, свойства полупроводника очень сильно зависят от того, какая долина расположена ниже – центральная, или одна из боковых. По этому признаку все полупроводники делятся на две группы прямозонные, для которых центральная долина ниже, и непрямозонные, для которых центральная долина выше. Дело в том, что электроны должны находится там, где энергия ниже, а следовательно переходы из зоны проводимости в валентную зону и обратно (переходы типа зона – зона) в прямозонных полупроводниках разрешены (справедливы законы сохранения энергии и импульса). Избыток энергии или недостаток ее компенсируется за счет излучения или поглощения кванта света. А в непрямозонных полупроводниках эти переходы запрещены законом сохранения импульса. При этом на несколько порядков снижается коэффициент поглощения света. А излучательные переходы из зоны проводимости в валентную зону, запрещенные по той же причине, практически не реализуются. В зависимости от состава твердого раствора положение долин меняется, но характер их взаимного расположения остается неизменным. Это особенность конкретной системы. Для других систем возможна реализация прямозонной энергетической диаграммы для любых состав твердых растворов или для определенного диапазона составов. Так на следующем апплете (см. замечание выше) показаны аналогичные зависимости для системы GaAs – AlAs. Здесь ситуация несколько красивее. Картина долин в разрешенных областях, в общем, похожа на предыдущую, только для чистого арсенида галлия и для твердых растворов, обогащенных арсенидом галлия центральная долина оказывается ниже, и полупроводники такого состава являются прямозонными. В области составов, обогащенных арсенидом алюминия, боковые долины оказываются ниже центральной, и материал становится непрямозонным. Одно из последствий такого поведения долин – из прямозонных материалов можно делать светодиоды и гетеролазеры, а из непрямозонного кремния, при всем желании этого сделать, пока не удается. С чем это связано будет понятно из раздела, посвященного процессам генерации и рекомбинации неравновесных носителей тока.

к началу раздела

Геометрический смысл второй производной и эффективная масса.

Напомним –первая производная соответствует тангенсу наклона касательной в точке. Равенство нулю первой производной – точка экстремума. По знаку второй производной определяется тип экстремума. А вот абсолютная величина второй производной содержит информацию о скорости изменения первой, т.е. об «остроте» экстремума. Более строго, кривизна в точке задается выражением:

2.3

здесь K – кривизна зависимости y =( x ), y ’ y ’’ – первая и вторая производные.

Рассмотрим теперь зависимость энергии от импульса для классической частицы:

2.4

Продифференцируем дважды эенергию по импульсу:

2.5

Т.е чем больше по вторая производная энергии по импульсу, тем , с одной стороны уже минимум зависимости . С другой стороны – меньше масса частицы.

Аналогичное рассмотрение можно провести для кристалла. Но в этом случае задача будет несколько сложнее. Отличия будут связаны с понятием импульса и массы. Вместо них придется пользоваться соответственно квазиимпульсом и эффективной массой. Кроме того, кристалл анизотропен и вторая производная от энергии по квазиимпульсу для изоэнергетической поверхности в пространстве квазиимпульсов будет тензором второго порядка, соответственно и эффективная масса будет тензором второго порядка:

2.6

При правильном выборе системы координат этот тензор становится диагональным, недиагональные члены оказываются равными нулю:

2.7

Компоненты тензора эффективной массы связаны таким образом с формой поверхности в трех главных сечениях в пространстве квазиимпульса (в первой зоне Бриллюэна).

Положение осложняется еще и тем, что для каждой из разрешенных зон таких зависимостей три, следовательно, появляется достаточно много сортов носителей с различными массами, каждая из которых тензорная. Выход из положения находят обычно несколькими способами. В наиболее простых случаях можно ограничиться приближением «сферических изоэнергетических поверхностей», т.е. пользоваться скалярной эффективной массой. Более строгий подход – для каждого типа задач вводится специфическое для этого типа задач значение скалярной эффективной массы. Так в разделе, посвященном равновесной статистике мы столкнемся с понятием «эффективной массы плотности состояний».

Существование нескольких сортов частиц с различной эффективной массой действительно наблюдается в эксперименте при исследовании циклотронного резонанса.

к началу раздела

1.4. Циклотронный резонанс

Мы получили, что в соответствии с формой энергетических зон эффективные массы электронов и дырок имеют несколько значений для каждой из разрешенных зон. Этот факт непосредственно подтверждается в различных экспериментах. Мы рассмотрим один из них, причем достаточно наглядный.

Пусть пластина полупроводника вырезана из кристалла с определенной ориентацией граней относительно кристаллографических плоскостей. Расположим эту пластину в магнитном поле с индукцией B. На электроны движущиеся в пластине с тепловыми скоростями действует сила Лоренца:

2.8

При наличии у тепловой скорости составляющей, перпендикулярной вектору магнитной индукции электрон будет двигаться по сложной траектории, но в плоскости перпендикулярной вектору B проекция этой траектории будет окружностью. Условием движения по окружности будет равенство центробежной и центростремительной сил, в роли последней выступает сила Лоренца:

2.9

Если сократить левую и правую часть последнего равенства на и учесть, что / r есть угловая скорость вращения в плоскости перпендикулярной B, то получим, что все электроны участвуют во вращательном движении с частотой:

,

2.10

которая называется циклотронной частотой. Если в кристалл ввести электромагнитное поле с такой же частотой, то электроны будут ускоряться под действием электрической составляющей этого поля и , соответственно, энергия электромагнитной волны будет поглощаться.

Интенсивность пика поглощения будет зависеть от того, как долго без столкновений с дефектами решетки могут двигаться электроны. Если электрон успевает за время свободного пробега сделать два полных оборота, пик поглощения становится достаточно четким (см Рис.1.1.)

Рис.2.1. Острота максимума поглощения при циклотронном резонансе в зависимости от времени свободного пробега (при постоянной циклотронной частоте).

Чтобы обеспечить достаточно большое время свободного пробега, нужно работать с совершенными и очень чистыми кристаллами и при очень низкой температуре ( обычно при 4,2° К — температуре жидкого гелия).

Схема эксперимента выглядит таким образом - пластину полупроводника помещают в волновод, который находится в свою очередь в магнитном поле соленоида. В волноводе создается СВЧ волна постоянной частоты. Индукцией магнитного поля управляют изменением тока через соленоид. Измеряют поглощение СВЧ волны на выходе из волновода. Меняя поляризацию волны и ориентацию пластины в серии экспериментов можно получить информацию о всех возможных значениях компонентов тензоров эффективно массы электронов и, совершенно аналогично, дырок. Тем самым удается получить информацию о форме различных долин для зоны проводимости и валентной зоны исследуемого полупроводникового материала.

.

Рис.2.2. Результаты измерения поглощения для пластины германия.

Каждому пику поглощения соответствует ансамбль частиц с определенной эффективной массой

Видны три пика поглощения связанные с тремя типами электронов, различающимися по эффективной массе и двумя типами дырок. Причем эти величины соответствуют одной ориентации пластины и одной поляризации электромагнитной волны, т.е. все относятся к одной компоненте тензора эффективной массы.

к началу раздела

Некоторые свойства эффективной массы.

Частицы (электроны и дырки) в кристалле под действием внешних сил двигаются с ускорением в полном соответствии с вторым законом Ньютона, причем роль инерционной массы исполняет эффективная масса. Размерность эффективной массы совпадает с размерностью обычной массы. А вот по величине такого совпадения нет – эффективная масса может быть больше массы свободного электрона, а может быть и значительно меньше. И это не связано с релятивистскими эффектами. На самом деле эффективная масса это некоторая характеристика легкости перехода частицы от одного узла к другому за счет туннелированния через потенциальный барьер между этими положениями. Более того, эффективная масса «дырок», как квазичастиц, вообще отрицательна.

к началу раздела

Теория мелких примесных состояний в полупроводниках

В общем случае вычисление энергии примесных центров в полупроводниковом кристалле оказывается чрезвычайно сложной задачей. Однако для однозарядных центров, соответствующих «эффективным» донорам и акцепторам –элементам V и III групп таблицы Менделеева этот расчет можно выполнить довольно просто, воспользовавшись водородоподобной моделью.

Предположим, что один из узлов в кристалле кремния замещен атомом мышьяка, имеющим пять валентных электронов. Четыре из них будут участвовать в образовании ковалентной "связи с ближай­ шими соседними атомами кремния. Пятый электрон, не принимая участия в образовании парноэлектронной связи, будет взаимо действовать с большим числом атомов кремния, и в результате он оказывается сравнительно слабо связанным с ионом мышьяка силами кулоновского взаимодействия. Его поведение подобно поведению электрона в атоме водорода. Однако при решении задачи о вели чине потенциала ионизации электрона примеси следует учесть дополнительно два обстоятельства. Во-первых, этот электрон находится не только в кулоновском поле иона мышьяка, но и в пе риодическом поле кристаллической решетки. В связи с этим для него необходимо учитывать не обычную массу, а эффективную массу т*. Во-вторых, взаимодействие между электроном и положитель ным ионом мышьяка с зарядом + Ze происходит в твердом теле, обладающем диэлектрической проницаемостью , поэтому в выра жение для потенциальной энергии электрона примеси следует ввести величину . Она будет равна:

2.11

где эпсилон с индексом 0 – абсолютная диэлектрическая постоянная, без индекса - относительная диэлектрическая постоянная кристалла.

Соотношение справедливо только для макроскопических точечных зарядов, другими словами, оно справедливо в том случае, если расстояние между взаимодействующими зарядами достаточно велико, т.е. орбита электрона примеси должна охватывать большое число узлов кристаллической решетки.

С учетом сказанного уравнение Шредингера для электрона атома мышьяка, не участвующего в образовании валентных связей, можно записать в виде:

2.12

Решив это уравнение по аналогии с уравнением для атома водор ода, получим выражение для собственных значений энергии элект рона примеси:

2.13

где энергия электрона отсчитывается от дна зоны проводимости. Эту формулу можно записать следующим образом:

2.14

Если подставить численное значение е, т, h , e 0 и выразить' энергию в электрон-вольтах, то получим:

2.15

где 13,52 соответствует величине в электрон-вольтах энергии иони зации атома водорода; есть энергия основного состояния (п = 1) атома донорной примеси.

Из последнего выражения следует, что уровень энергии донорной примеси, соответствующий основному состоянию (п =1), лежит в запрещенной зоне полупроводника ниже дна зоны проводимости Е с на величину E d .

Энергия ионизации донорной примеси (Е с- E d ) согласно последнему ра венству в раз меньше энергии ионизации атома водорода, Кроме того, энергия ионизации зависит от

. Это означает, что уровень двукратно заряженного иона донорной примеси расположен в запрещенной зоне ниже уровня однократно заряженного иона этой примеси.

Если положить т* = 0,25 т, то в случае германия, у которого = 15,8, энергия ионизации пятивалентных атомов примеси должна быть порядка 0,01 эв. Как следует из таблицы величина энергии ионизации, полученная экспериментально, хорошо согласуется с рассчитанным значением:

 

Примесь	Тип центра	Энергия ионизации примесей элементов III и V групп в кремнии и германии eV
		Ge	Si
B	A	0.0104	0.045(T)	0.046(O)
Al	A	0.0102	0.057(T)	0.067(O)
Ga	A	0.0108	0.065(T)	0.071(O)
In	A	0.0112	0.16(T)	0.154(O)
P	D	0.0120	0.044(T)	0.046(O)
As	D	0.0127	0.049(T)	0.056(O)
Sb	D	0.0096	0.039(T)	0.043(O)

Расчет радиуса орбиты электрона примеси по водородоподобной модели дает формулу:

2.16

Радиус первой орбиты электрона донорной примеси в германии согласно выражению составляет величину а1= 60 а0 = 32 ( ao – радиус первой боровской орбиты для атома водорода). Если учесть, что постоянная решетки германия равна 5,62 , то эта орбита охватывает приблизительно 200 узлов решетки. Это под тверждает возможность рассмотрения движения электрона примеси в среде с постоянной диэлектрической проницаемостью.

Аналогичные вычисления можно провести для дырок, расположенных вблизи атома элемента III группы таблицы Менделеева. В этом случае система ион – дырка напоминает модель атома антиводорода – позитрония. Результаты расчета и эксперимента приведены в той же таблице.
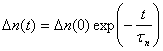
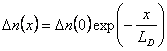