Первая зона Бриллюэна полупроводника типа алмаза

Итак, для полного описания всей совокупности состояний электрона в кристалле достаточно рассмотреть только область значений k, ограниченную первой зоной Бриллюэна.

Первая зона Бриллюэна представляет собой элементарную ячейку Вигнера – Зейтца для обратной решетки, растянутой в 2 раз(рис.3). Для определения вида первой зоны Бриллюэна нужно построить обратную решетку с параметрами ячейки и построить в ней ячейку Вигнера-Зейтца.

17-18. Энергетический спектр электронов в кристалле. Модель Кроннига – Пенни.

Для нахождения энергетического спектра электронов в кристалле необходимо решить одноэлектронное уравнение Шредингера с периодическим потенциалом решетки V(r).Собственные функции 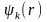и собственные значения 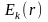этого уравнения зависят от вида периодического потенциала. В тоже время точный вид V(r) определить практически невозможно. В этих условиях для нахождения решения уравнения Шредингера приходится применять различные предположения относительно вида функции V(r).

Следуя Кронигу и Пенни рассмотрим простую одномерную модель. В этой модели зависимость потенциальной энергии электрона от расстояния х для одномерной решетки можно представить следующим образом:

Здесь прямоугольные потенциальные ямы шириной a чередуются с прямоугольными барьерами шириной b. Период такой решетки c=a+b.

Таким образом, потенциальная энергия представляет собой функцию:

V (x)=0 nc<x<nc+a V(x)=V₀ nc+a<x<(n+1)c

Здесь n – любое число (0, )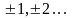

Запишем одноэлектронное уравнение Шредингера для одномерного случая

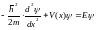(2.18)

Решение этого уравнения будем искать в виде функции Блоха

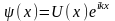(2.19)

где U(x) – периодическая функция с периодом решетки, т.е.

U(x)=U(x+c)=U(x+2c)=… (2.20)

Найдем уравнение, которому должна удовлетворять функция U(x). Подставив (2) в (1) получим для области 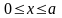, а также для любой ямы

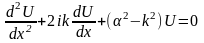(2.21)

и для области 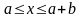(или любого другого потенциального барьера)

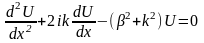(2.22)

где 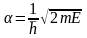и 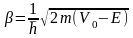(2.23)

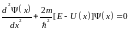
В области , где V(x)=0 имеем:

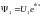
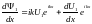
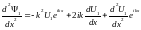
Вводя параметр: 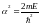; 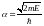получаем:

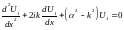
В области потенциал

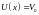
Обозначив 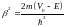получаем:

.

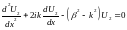Решение уравнения имеет вид:

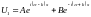
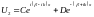
Где A, B, C, D постоянные коэффициенты функции U, и 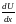должны быть непрерывны и U(a)=U(-b)

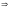
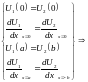решая эти уравнения получаем:

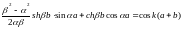
Решение уравнения (2.21) и (2.22) имеют вид

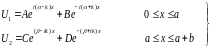(2.24)

Последние выражения содержат четыре неизвестных A,B,C,D, которые находят из условия непрерывности

приx=n(a+b)

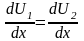приx=a+n(a+b) (2.25)

Записывая (2.25) с учетом (2.24), нетрудно убедится, что условие существования нетривиального решения системы задается уравнением:

(2.26)

Уравнение (2.26) связывает величины и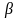 , содержащие собственные значения энергии электрона Е, с волновым вектором 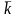. Таким образом, равенство (2.26) можно рассматривать как соотношение между Е и К.

Решить уравнение (2.26) очень сложно. Поэтому вводят дополнительно упрощающие предположения.

Пусть 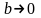, а 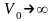, но так, чтобы произведение ширины барьера на высоту в V₀ оставалось конечным причем 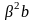- конечно, 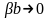, (т.е. мы рассматриваем тонкие высокие барьеры).При , ,

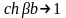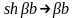
Таким образом, вместо (2.26) можно записать

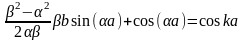(2.27)

или

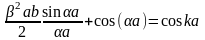(2.28)

Обозначим Р=lim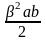 (2.29)

Величина Р представляет собой меру эффективной площади каждого барьера. Он характеризует степень прозрачности барьера для электрона или, другими словами степень связанности электрона в потенциальной яме. С учетом этого можно записать

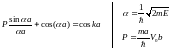(2.30)

В правой части стоит функция cos. Она четная. Замена к на(-к) не меняет уравнение (2.30). Это означает, что энергия электрона также является четной функцией к, то есть

Е(-к)=Е(к) (2.31)

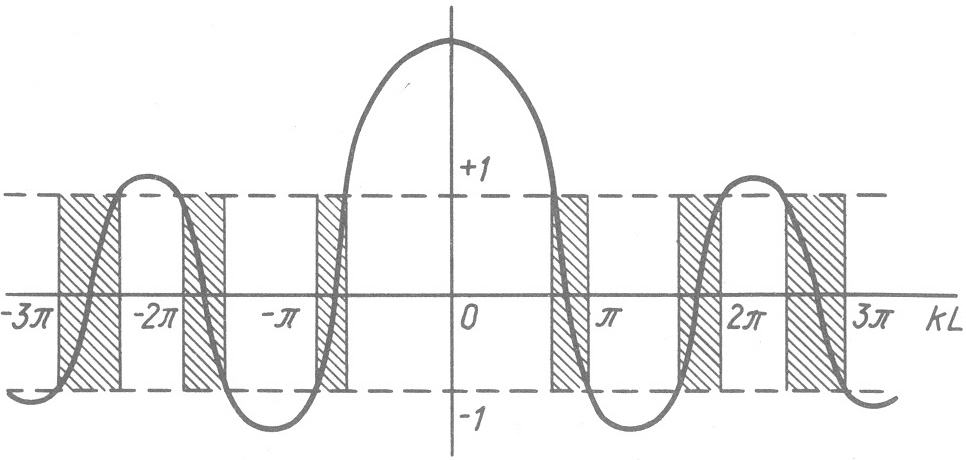
Рис.5.зрешенные (заштрихованные) и запрещенные (светлые) зоны для Кронига – Пенни.

Решить уравнение (2.30) можно графически. Зависимость левой части уравнения от параметра можно изобразить таким образом

Поскольку coska, стоящий в правой части, может принимать только значения от –1 до +1, то допустимыми значениями являются такие, для которых левая часть уравнения не выходит из указанных пределов.. На рис. интервалы разрешенных значений заштрихованы. Ширина этих интервалов зависит от параметра Р. Чем меньше Р, тем они шире. Кроме того, их ширина зависит и от . При любом фиксированном значении Р эти интервалы расширяются с увеличением .

Таким образом, учитывая связь  с Е, можно заключить, что энергия электрона в кристалле не может принимать любого значения. Есть зоны разрешенных и запрещенных энергий, которые можно изобразить так, как показано на рис.

Рассмотрим как изменяется спектр в двух предельных случаях: Р 0 и

Р .

Первый случай (Р 0) соответствует условию V₀ 0, то есть почти свободному электрону (приближение слабой связи).

Из соотношения (2.30) следует, что =к. С учетом формулы (2.13) можем записать:

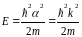
Последнее выражение совпадает с зависимостью Е (к) для свободного электрона.

Второй предельный случай (Р в силу того что V₀ 0) соответствует локализации электрона в бесконечно глубокой яме, то есть электрон сильно связан (приближение сильной связи). При Р из уравнения (2.30) находим:

sin( )/( )=0 (2.32)

то есть

a = nгде n= 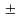1; 2; 3;….. (2.33)

Тогда:

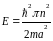(2.34)

Таким образом, при Р система энергетических зон вырождается в дискретные уровни.

Для электрона, движущегося в периодическом поле решетки, явный вид закона дисперсии Е(к) можно найти, решив уравнение (2.30). Это можно сделать, допустив, что Р>>1. Такое предположение соответствует случаю сильной связи. В приближении сильной связи выражение для энергии электрона в кристалле имеет вид:

E=E_on-C_n+(-1)ⁿA_ncoska (2.35)

(-энергетические уровни опускаются, E<E_0n=> энергетически выгодно объединение атомов в цепочку)

где 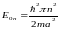- энергия n–го энергетического уровня электрона в изолированной бесконечно глубокой яме.

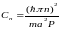- (мал, т. к. P>>1) (2.36)

A_n - коэффициент, в общем случае не равный С_n.

Второй и третий члены отражают действие периодического поля решетки. Видно, что в периодическом поле решетки энергетические уровни опускаются на значение С (перед С стоит знак -). Это свидетельствует о том, что объединение атомов в цепочку выгодно. Третий член определяет в (2.35) зонный характер энергетического спектра.

Зависимость Е(к) для электрона, находящегося в одномерной решетке имеет вид:

То есть для всех к, отличающихся на ( 2n /a) энергия одна и таже. Интервал значений от - /a до /a представляет первую зону Бриллюэна. Два отрезка от - 2 /a до - /a и от /a до 2 /a вторую зону Бриллюэна и так далее.

(************картинки конспект стр. 36**********обр. стр.)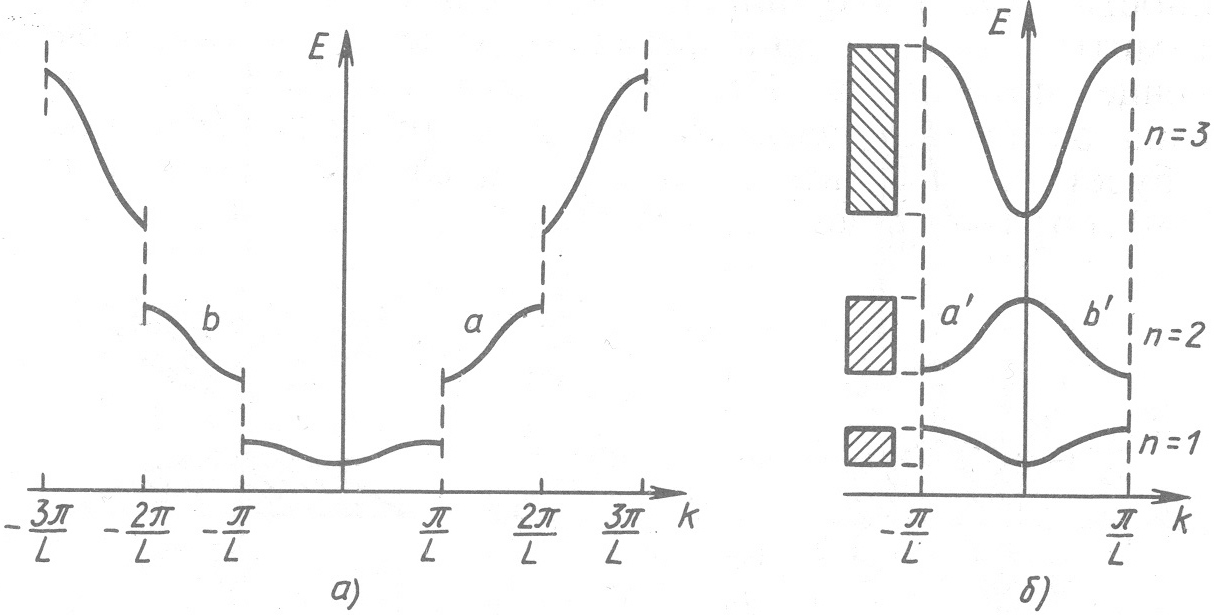

Рис.6.Обычное представление функции E(k) для простой одномерной кристаллической структуры в соответствии с моделью Кронига – Пенни (а), и приведение функции E(k) к первой зоне Бриллюэна (б). Заштрихованы разрешённые зоны, не заштрихованы – запрещённые зоны.

Волновая функция Блоха- переодична.

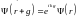
Если 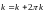, где 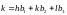- вектор обратной решетки.

Следовательно, состояния, характеризующее волновым вектором и 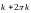эквивалентны. Т. е. энергия электронов находящихся в этих двух состояниях одинакова.

Другими словами: и волновая функцияи энергия электронов, находящихся в кристалле является периодическими функциями волнового вектора с периодом

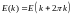
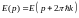
Если в -пространстве (или в 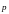-пространстве ) построить обратные решетки с векторам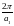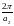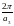и ; ; или 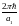; ; 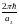; 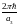то все -пространство можно разделить на области, в которых имеются физически эквивалентные состояния. Эти области называются зонами Бриллюэна.

Зависимость Е(к) часто строят только для первой зоны Бриллюэна. Такой способ изображения Е(к) получил название схемы приведенных зон, в отличие от первого, называемого периодической зонной схемой.

Кроме этих двух способов используют еще один, получивший название расширенной зонной схемы. Здесь различные энергетические зоны размещаются в к-пространстве в различных зонах. Зависимость Е(к) для свободного электрона представлена тонкой линией. Разрывы в энергетическом спектре электрона, как видно из рисунка, появляются на границах зон Бриллюэна.

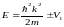, где 2V₁=E_g - запрещенная зона

Зонная структура в трехмерном случае может быть сложнее, чем в рассматриваемой одномерной модели. Как правило, зависимость Е(к) в трехмерном кристалле различна для разных направлений в зоне Бриллюэна. Это связано с тем, что трехмерный потенциал П(r), зависящий от структуры кристалла, в различных направлениях не одинаков. Следствием этого может быть перекрытие разрешенных зон, или запрещенная зона в одном направлении может совпадать с разрешенной зоной в другом направлении.