13. Качественная модель зонной структуры твердого тела.

Согласно модели Бора электроны в изолированном атоме вращаются вокруг ядра по круговым орбитам (оболочкам), каждой из которых соответствует определенный энергетический уровень. Последовательность энергетических уровней, которые может занимать электрон, находящийся под воздействием кулоновского потенциала атомного ядра, задается соотношением:

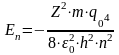, (2.1)

где Z – число протонов в ядре, m – масса свободного электрона, _ – диэлектрическая проницаемость вакуума, h – постоянная Планка,n – положительное целое число, q₀ – заряд электрона.

На каждой оболочке может находиться строго индивидуальное число электронов. Переход электрона с одной оболочки на другую возможен при поглощении или испускании кванта электромагнитного излучения с энергией, равной разности энергий уровней, между которыми перемещается электрон. Поэтому оптические спектры поглощения атомов, соответствующие электронным переходам с одного уровня на другой, также должны быть дискретны.

При низких температурах, если с атомом связано более одного электрона, электроны заполняют разрешенные уровни, начиная с низких значений энергии. В соответствии с принципом Паули один энергетический уровень могут занимать не более двух электронов с противоположными спинами.

Очевидно, что в кристалле, представляющем собой совокупность близко расположенных атомов, энергетические уровни электронов в каждом из атомов должны измениться. Причиной этого является появление новых сил взаимодействия между ядрами, между электронами, принадлежащими разным атомам, и между всеми ядрами и всеми электронами, тогда как в изолированном атоме существуют только сила притяжения ядром атома всех своих электронов и сила отталкивания между электронами.

14. Уравнение Шредингера для кристалла.

Возможные значения энергии электрона в кристалле можно найти из решения уравнения Шредингера для стационарных состояний, которое в общем случае имеет вид:

H = E, (2.2)

где H – оператор Гамильтона для кристалла, E – полная энергия кристалла,  - волновая функция кристалла.

Волновая функция имеет следующий вид:

.

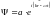Комплексно-сопряженная волновая функция:

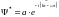
Квадрат амплитуды волновой функции характеризует вероятность 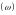нахождения электрона в данной точке пространства, определяемой радиус-вектором .

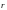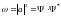
Квадрат модуля волновой функции, умноженный на элемент объема 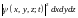есть вероятность обнаружить электрон в момент времени t в объеме 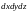, образующий бесконечно малую окрестность точки .

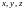При этом уравнение Шредингера должно быть дополнено ограничениями, накладываемыми на волновую функцию:

• волновая функция должна быть конечной (так как вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

• производные /x, /y, /z должны быть непрерывны

• функция ² должна быть интегрируема. Это условие в простейших случаях сводится к условию нормировки вероятностей:

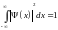
2.2 Уравнение Шредингера для кристалла

Твердое тело представляет собой единую систему легких (электронов) и тяжелых (ядра) частиц. Наиболее полные сведения о свойствах такой системы, в том числе и об ее энергетическом спектре, можно получить решая уравнение Шредингера, соответствующее стационарным состояниям этой системы. Но, из-за того, что в кристалле имеет место большое число взаимодействий, уравнение Шредингера приобретает сложный вид:

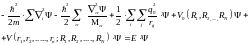(2.3)

В уравнение (2.3) входят следующие виды энергии:

1) Кинетическая энергия электронов:

,

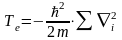где 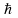-постоянная Дирака, равная постоянной Планка h, деленной на 2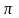 ( = h/2 ), m-масса электрона, а 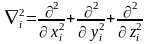- оператор Лапласа для i-го электрона;

2) Кинетическая энергия ядер

,

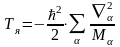где 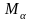-масса ядра;

3) Потенциальная энергия попарного взаимодействия электронов между собой ,

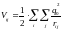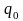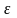где -заряд электрона , - диэлектрическая проницаемость кристалла , 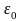- электрическая постоянная;

4) Потенциальная энергия попарного взаимодействия ядер между собой

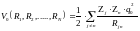
5) Потенциальная энергия взаимодействия электронов с ядрами: ,

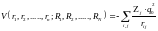где 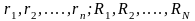- координаты электронов и ядер соответственно;

6) Полная энергия кристалла E .

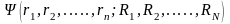- собственная волновая функция кристалла, зависящая от координат всех электронов и атомных ядер.

Уравнение (21) содержит 3N(Z+1) независимых переменных, где N – число атомов в кристалле, Zq₀ – заряд ядра. Число атомов в 1 см³ составляет примерно 5*10²² и каждый атом содержит большое число электронов. Следовательно, волновая функция зависит от огромного числа (10²⁴-10²⁵) независимых переменных. Точное решение уравнения Шредингера невозможно даже для отдельных атомов, за исключением атома водорода. Поэтому задача сводится к нахождению приближений в рамках физически оправданных упрощающих предположений. Зонная теория, лежащая в основе современной физики полупроводников, базируется на двух приближениях.