29. Закон действующих масс

Исключим уровень Ферми, перемножив n и p:

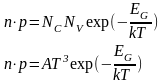(15)

(16) Правая часть зависит только от температуры и

ширины запрещ. зоны полупроводника.

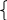Но! Не зависит от концентрации.

np=n²_i=p²_i=const (17) n_i и p_i –собственные концентрации носителей;

Уравнение (17) называют уравнением полупроводника или законом действующих масс.

Произведение концентраций основных и не основных носителей заряда в невырожденном полупроводнике при фиксированной температуре является постоянной величиной, которая не зависит от концентрации введённой примеси и равна квадрату концентраций собственных носителей заряда при той же температуре.

{Ввести понятия основных и неосновных носителей заряда; понятие энергии неосновных носителей заряда.}

С помощью формулы (16) можно найти, что в Siпри Т_комн. 1 электронно-дырочная пара приходится на 7,3*10¹¹атомов.

Т_комн: GaAs:n≈10⁷ ;E_g=1.41eV

Si: n≈10¹⁰ ;E_g=1.12eV

Ge: n≈3*10¹³ ; E_g=0.67eV

^{1 000K 500 300 200}

10¹⁹

10¹⁷

10¹⁵

10¹³ GaAs Ge

10¹¹Si

10⁹

10⁷

Si: n_i N_Si=5*10²²ат/см³

T=300K n_i~10¹⁰ см^-3

T=500K n_i~10¹⁴ см^-3

T=1000Kn_i~10¹⁸ см^-3

30. Собственном полупроводнике

Напомнить: что такое примесный и собственный полупроводник §2.6.3 стр. реальных п/п-в

В собственном полупроводнике каждый электрон, перешедший в зону проводимости, оставляет дырку в валентной зоне. Поэтому: n=p. Тогда:

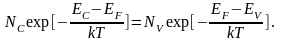
Если определить за нулевую энергию верх валентной зоны, т.е. E_V=0 =>E_C=E_V+E_G=E_G.

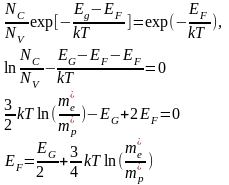логарифмируя:

(14)

Уровень Ферми при абсолютном нуле расположен посередине запрещённой зоны!

kT при Т_комн≈0,026 эВ. Поэтому, если эффективные массы электронов и дырок различаются не очень сильно, то уровень Ферми находится приблизительно посередине, между E_VиE_C

31. Зависимость положения уровня Ферми от концентрации примеси и температуры.

Повторить немного о легировании (атомы V и III группы в кремнии). Расположение донорного и акцепторного уровней в запрещённой зоне!!! Соотношение концентрации атомов примеси и собственных атомов.

А. Влияние концентрации.

Для того, чтобы определить влияние концентрации примеси на положение уровня Ферми, нужно в общем случае решить следующее уравнение общей электронейтральности:

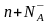
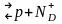(17)

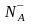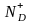где -- число ионизованных акцепторных атомов (которые захватили электрон из валентной зоны); -- число ионизованных донорных атомов (которые отдали электрон в зону проводимости).

Для решения этого уравнения нужно подставить выражения для n_i, p_i, и N_A, N_D.

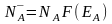
(18)

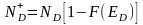
где F(E_A) – вероятность того, что электрон находится на акцепторном уровне А;

1-F(E_D) – вероятность того, что электрон не находится на донорном уровне D.

В общем случае Вы можете попробовать подставить эти значения и решить его. Мы же здесь приведём решение для случая, когда 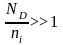(т.е. уровень легирования очень высокий по сравнению с собственной концентрацией электронов).

n>>p, N_D>>N_A =>n≈N_D

В этом случае n≈N_D≈N_Cexp(-(E_C-E_F)/kT), откуда E_F≈ E_C –kTln(N_C/ N_D). Аналогично для р-типа полупроводника E_F≈ E_V +kTln(N_V/ N_A).

В кремнии при Т_КОМН:

N _C =2,8 • 10¹⁹ см^-3 Различаются

N_V =10¹⁹ см^-3 эффективные массы !!!

Т.е. в этих случаях (поскольку N_V<N_A и N_C<N_D) энергия Ферми располагается вблизи границ разрешённых зон (соответственно зоны проводимости и запрещённой зоны).

Говорят, что полупроводник является вырожденным, если концентрация примеси настолько высока, что уровень E_F находится на границах разрешённых зон.

Можно показать также, что в области малых концентраций легирующей примеси E_F≈ lnN_D, т.е. E_F растёт с увеличением N_D по логарифмическому закону (достаточно медленно).

Таким образом, графически можно изобразить положение E_F от концентрации примеси следующим образом:

E

E_C

- E_F , T=0, N_D=0

E_V

l nN_D lnN_A

Б. Как изменяется положение уровня Ферми в примесном полу проводнике от температуры ?

В общем случае этот вопрос достаточно трудно описать математически, т.к. E_Gи E_Dзависят от периода решётки и связаны с температурой, но этот эффект мы учитывать не будем.

Рассмотрим 2 крайних случая:

Соотношение концентраций примеси и собственных атомов !!!

1. при очень низких температурах ионизация собственных носителей не происходит (по сравнению с примесными). Поэтому E_F и E_Fi будет находиться посреди E_D и E_G;

2. при очень высоких температурах можно предположить, что почти все собственные атомы ионизованы, т.е. концентрация электронов и дырок приблизительно равна объёмной концентрации собственных атомов. Концентрация примеси – невелика. Следовательно, E_F к E_Fi. На картинке это выглядит следующим образом:

E

E _C

E _D

E_Fi N_D2 > N_D1

E _A

E_V

T

В свою очередь E_Fi будет увеличиваться как :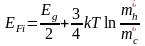

С ростом температуры ширина запрещённой зоны уменьшается. Качественно причину этого можно представить следующим образом: при более высокой температуре тепловое движение атомов в решётке становится более энергичным, период решётки оказывается менее определённым (чётким) и взаимодействие ослабевает (т.е. уменьшается энергия связи электрона с атомом решётки), а следовательно и E_G.

С ростом ТE_F в собственном полупроводнике уходит к E_C:

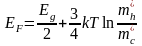
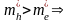рост E_F