§ 28. Концентрация электронов и дырок

Теперь можно определить концентрацию носителей заряда в полупроводнике. Мы знаем, сколько у нас имеется состояний (свободных энергетических уровней), а также с какой вероятностью эти состояния заняты электронами. Поэтому в диапазоне энергий между E и E+dE количество электронов будет:

dn=N(E)*F(E) dE(11)

Для всей зоны проводимости число электронов, приходящихся на единицу объёма:

.

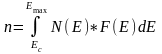Интегрирование проводится в пределах от нижней границы зоны проводимости E_c, до верхней границы этой зоны E_max. Сохраняя правильный смысл результата, можно существенно упро­стить выкладки, положив, что верхний предел интегрирования равен +∞. Выполнив соответст­вующие подстановки, получим:

;

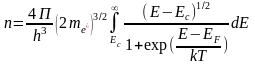Мы будем полагать, что E>>E_F, т.е. энергия электронов превышает E_F настолько, что E-E_F>>kT. Тогда распределение Ферми-Дирака переходит в распределение Максвелла-Больц­мана:

.

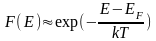Тогда:

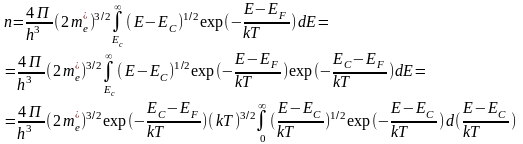
[dE→d(E-E_C)]

Положим: 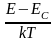=x; тогда 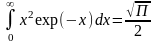(табличный)

(12)

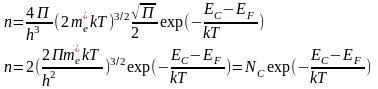
Аналогичные вычисления можно провести для концентрации дырок [исключения: вероятность возникновения вакантного уровня равна 1-f(E)], а интегрирование проводится от -∞ до E_V. От­куда:

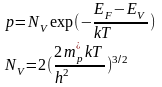(13)

Физический смысл параметров N_V и N_C:

N_V и N_C—эффективные плотности уровней в зоне проводимости и валентной зоне соответ­ственно.

Рассмотрим графическое определение концентрации носителей заряда (электронов и дырок) в зоне проводимости и валентной зоне в зависимости от температуры:

E EE

-- электроны

E_C * E_C= E_C

--T>0

E _F E_F E_F

--T=0

E _V * E_V = E_V

-- дырки

(а) N(E) (б)F(E) (в) n=N(E)*F(E)

(а)- графики функций, описывающих плотность уровней;

(б)- функция распределения; вероятность, с которой уровни оказываются занятыми при

Т=0 и Т>0;

(в)- произведение этих функций, показывающее распределение носителей заряда в зонах.

при Т=0, произведение N(E)*F(E)=0 для E>E_C

N(E)*F(E)=N(E) для E<E_V

т.е. электроны отсутствуют в зоне проводимости,

валентная зона заполнена полностью.

2) при Т>0, электроны, оказавшиеся в зоне проводимости распределяются по закону

N(E)*F(E), а дырки, возникшие в валентной зоне, -- по закону N(E)[1-F(E)].

!!! Число электронов в зоне проводимости равно количеству дырок в валентной зоне.

3) если в запрещенной зоне имеются уровни, то вероятность их заполнения очень велика.