24. Плотность квантовых состояний.

Наиболее важной характеристикой электронного энергетического спектра является распределение электронных состояний по энергиям. Количественно описать это распределение можно, используя понятие "плотность состояний".

Пусть в кристалле единичного объема в интервале энергий от Е до Е+dE имеется dZ квантовых состояний (безучета спина). В выбранном интервале энергииdE=const при различных значениях величины энергии Е число состояний dZ может различаться. Поэтому будем считать, что

во-первых, dZ зависит от величины Е, то есть dZ = dZ (Е);

во-вторых, связь между dZ и dE задается соотношением

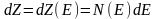, (2.1)

где коэффициентN, называемый плотностью состояний, также зависит от величины Е.

Физический смысл плотности состояний очевиден. Из соотношения (2.1) следует:

N(E)=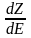 , (2.2)

следовательно, плотность состояний – это число состояний в единичном интервале энергий для единичного объема кристалла.

Расчет величины N(Е) является довольно сложной квантовомеханической задачей, так как ее значениетесным образом связано с фор­мой изоэнергетических поверхностей. Действительно, построим в зоне Бриллюэна две изоэнергетические поверхности Е и Е+dE. Они выделяют некоторый слой в пространстве квазиимпульса (рис. 1). Пусть объем это­го слоя d_p, ему соответствует объем фазо­вого пространства, то есть пространства координатx, y, z и импульсов p_x, p_y, p_z

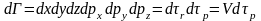(2.3)

Согласно принципа неопределенности Гейзенберга, минимальный объем фазовой ячейки, в которой может уместиться частица, равен h³_. . Следовательно, число фазовых ячеек в объеме фазового пространства dГ равно 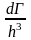, а число состояний для единичного объема

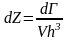. (2.4)

Учитывая соотношения (2.1) и (2.3) следует

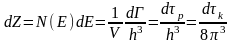(2.5)

Входящую в выражение (2.5) величину объема слоя в пространстве квазимпульса d_k(E,E+dE) можно найти, если известно уравнение изоэнергетических поверхностей.

Рассмотрим некоторые частные случаи.

1. Предположим, что изоэнергетические поверхности имеют форму сферы с минимальной энергией E_min в центре зоны Бриллюэна. Пусть

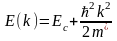(2.6)

Две изоэнергетические поверхности Е и Е+dЕ выделяют сферический слой толщиной dkи объемом d_k(Е, Е+dE) (рис. 1):

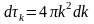(2.7)

Воспользовавшись соотношением (2.6), выразим kчерезE :

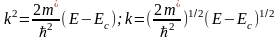(2.8)

Дифференцируя по k первое выражение в (2.9), получим

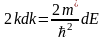(2.9)

Учитывая соотношения (2.7), (2.8) и (2.9), можем записать

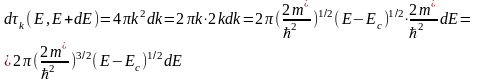(2.10)

Для dZ из (2.5) и (2.10) получим

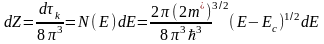(2.11)

или

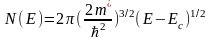(2.12)

Таким образом, если энергия носителей заряда является квадратичной функцией квазимпульса, то плотность состояний N(Е) имеет зависимость от энергии вида .

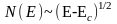§ 26-27. Функция распределения Ферми-Дирака.

Функция распределения - это функция, которая в условиях термодинамического равновесия пропорциональна вероятности того, что некоторая частица занимает определённый энергетиче­ский уровень Е.

Для нашего случая задача сводится к нахождению наиболее вероятного распределения частиц по энергии с учётом принципа Паули.

Решая такую задачу по статистической физике, можно получить распределения Ферми-Ди­рака.

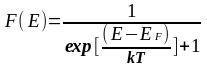; (8)

где Е_F –энергия Ферми.

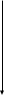
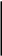
F(E)

--T=0

T=1000K-

T=600K-----

E

E_F=2.5eV

Основные свойства функции Ферми-Дирака:

]

E=E_F =>F(E)=0.5 - т.е. уровень Ферми занят с вероятностью 0,5 (всегда);

T=0, тогда: F(E)=1 для E<E_F

F(E)=0 для E>E_F

т.е. при Т абсолютного нуля все разрешимые состояния ниже уровня Ферми заняты, а все выше него - свободны. Это отличается от случая классических частиц, когда при Т=0 все электроны имеют Е=0.

Если энергия электронов значительно выше энергии Ферми, т.е. E-E_F>>kT, тогда

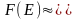
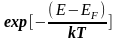(9)

Формула (9) представляет собой классическое распределение Максвелла- Больц­мана. Таким образом, функция Ферми-Дирака при больших энергиях переходит в распределе­ние Максвелла-Больцмана.

Если энергия электрона ниже Е_F настолько, E_F-E>>kT, тогда:

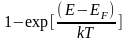(10)

т.е. в области энергий, существенно меньших E_F разрешённые состояния заняты с вероятностью, близкой к 1.

В области EE_F функция F(E) изменяется очень быстро от значений, близких к 1, до нуля. Скорость изменения зависит от kT, и для температуры абсолютного нуля равна бесконечности.