
- •Цель работы
- •Основные положения теории спектрального представления сигналов
- •Экспериментальное изучение спектров сигналов
- •Описание лабораторного оборудования
- •Содержание отчета о выполнении лабораторной работы
- •Контрольные вопросы
- •Библиографический список
- •Изучение частотных спектров сигналов Методические указания
- •18 Хабаровск 2012

Цель работы
Целью работы являются:
закрепление знания основ теории спектрального представления сигналов;
уяснение и закрепление в памяти закономерностей построения спект- ров периодических импульсных сигналов;
освоение навыков работы с анализатором спектра.
Результаты работы должны быть оформлены документально в виде отчета о выполнении лабораторного исследования.
Основные положения теории спектрального представления сигналов
Произвольная кусочно-непрерывная функция f (x) , для которой вы- полняется условие
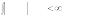
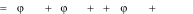 f
(x)
2
dx ,
может
быть представлена
в
виде ряда:
f
(x)
2
dx ,
может
быть представлена
в
виде ряда:
f (x) с0 0 (x) c1 1 (x) ... cn n (x) ... (1)
 Совокупность
функций 0
(x),
Совокупность
функций 0
(x),
нальную систему.
1 (x)...
n (x) представляет собой ортого-
Ряд (1) называется обобщенным рядом Фурье по данной системе n (x) .
Совокупность коэффициентов
с0 ,с1..., называемая спектром сигнала f (x) ,
полностью определяет этот сигнал.
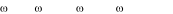 При
разложении
периодического
сигнала
s(t)
с
периодом
T
в
ряд
Фурье
в
качестве
ортогональной
системы
берут
совокупность
гармониче-
ских
колебаний
кратных
частот:
При
разложении
периодического
сигнала
s(t)
с
периодом
T
в
ряд
Фурье
в
качестве
ортогональной
системы
берут
совокупность
гармониче-
ских
колебаний
кратных
частот:
1, сos
0t,sin
0t,cos2
0t,sin2
0t,... ,
или (в комплексной форме)
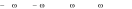 …
e
i
2
…
e
i
2
0t ,e i
0t ,1,ei
0t ,ei 2
0t ...

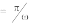 Интервал
ортогональности
совпадает
с
периодом
T 2
Интервал
ортогональности
совпадает
с
периодом
T 2
сигнала s(t) .
0
Предполагается, что функция s(t) имеет на интервале T 2,T 2 конеч- ное число разрывов, а также конечное число максимумов и минимумов.
Ряд Фурье в тригонометрической форме имеет вид:
 a
a
s(t) 0
2
(a n cosn 0t bn sin n 0t) . (2)
n 0
 Амплитуды
гармоник
определяются
для
всех
n 0
по
следующим
фор-
мулам:
Амплитуды
гармоник
определяются
для
всех
n 0
по
следующим
фор-
мулам:
 T
T
2 2
a n s(t)cosn
0 t dt ; (3)
T T 2
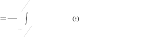 T
T
2 2
bn s(t)sin n
0 t dt . (4)
T T 2
Ряд Фурье в комплексной форме имеет вид:
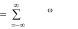
n
s(t) c ein0 t . (5)
n
Коэффициенты ряда определяются по формуле
 T
T
1 2
сn s(t)(cosn
0t isin n
0t)dt сnс
iсns . (6)
T T 2
Коэффициенты часто бывает удобно записывать в форме
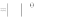 i
n
i
n
где
 c c2
c c2
c2 ,
arctg
cns
cn cn e , (7)
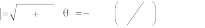 .
.
n nc ns n
cnc
Вместо выражения (2) нередко используют запись разложения в ряд Фурье следующего вида:
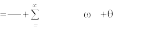 a
a
s(t) 0
An cos n 0t n
, (8)
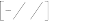
где An
2 сn , n
arctg
2 n 1
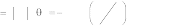 bn .
bn .
a n
Совокупность коэффициентов
A n , показывающую распределение интен-

 сивности
гармонических
колебаний
по
оси
частот,
определяют
как
амплитуд-
ный
(амплитудно-частотный)
спектр
сигнала.
Распределение
же
начальных
фаз
сигналов
n
по
оси
частот
называют
фазовым
спектром
сигнала.
сивности
гармонических
колебаний
по
оси
частот,
определяют
как
амплитуд-
ный
(амплитудно-частотный)
спектр
сигнала.
Распределение
же
начальных
фаз
сигналов
n
по
оси
частот
называют
фазовым
спектром
сигнала.
Если сигнал s(t) – четная функция времени, т. е. s(t) s(t) , то в
тригонометрической записи ряда остаются только косинусоиды, так как ко-
эффициенты bn
обращаются в нуль. Для нечетной функции s(t) , наоборот,
ряд состоит только из синусоид.
Спектр периодического колебания называется линейчатым или
 дискретным,
так
как
состоит
из
отдельных
линий,
соответствующих
дис-
дискретным,
так
как
состоит
из
отдельных
линий,
соответствующих
дис-
кретным частотам 0,
0 ,2
0 ... Расстояние по оси частот между компонента-
 ми
спектра
(линиями)
–
основной
частотный
интервал –
определяется
пе-
риодом
повторения сигнала:
ми
спектра
(линиями)
–
основной
частотный
интервал –
определяется
пе-
риодом
повторения сигнала:
 2
2
. (9)
T
 Наглядное
представление
о
взаимном
расположении
гармонических
со-
ставляющих
на
оси
частот,
распределении
их
интенсивностей,
ширине
час-
тотного
интервала,
где
сконцентрирована
энергия,
дает
графическое
изо-
бражение
спектра
амплитуд.
В
качестве
примера
на
рис.
1,
а
приведен
Наглядное
представление
о
взаимном
расположении
гармонических
со-
ставляющих
на
оси
частот,
распределении
их
интенсивностей,
ширине
час-
тотного
интервала,
где
сконцентрирована
энергия,
дает
графическое
изо-
бражение
спектра
амплитуд.
В
качестве
примера
на
рис.
1,
а
приведен
спектр коэффициентов
сn , а на рис. 1, б – спектр амплитуд An
2 сn
для
одного и того же периодического колебания.


а б
An|Cn|
a 0 a0
2
0 n 0 n
Рис. 1. Коэффициенты спектрального разложения (а) и амплитудный спектр (б) периодического сигнала
Не следует забывать, что изображение гармонической составляющей в виде линии достаточно условно. При строгом подходе амплитудно-частот- ный спектр следует изображать в виде совокупности точек (рис. 2). Абсцис-

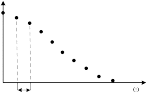 са
точки
соответствует
частоте
гармони- An
са
точки
соответствует
частоте
гармони- An
ческой составляющей n
0 , ордината –
ее амплитуде
A n .
Ограничение ряда, аппроксими- рующего сигнал s(t) , конечным числом членов приводит к отклонениям формы
результирующего колебания
sn (t) от ис- 0
ходного. К примеру, на рис. 3 показана форма колебания, образованного гармо- никами с 1-й по 7-ю разложения последо- вательности прямоугольных импульсов в
Ω
Рис. 2. Точечное представление амплитудного спектра сигнала
ряд Фурье. Отличия сигнала возникают, главным образом, вблизи разрывов функции – переднего и заднего фронтов импульса.
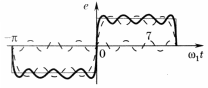
Рис. 3. Импульс, образованный семью компонентами ряда Фурье
Рассмотрим спектры сигналов, которые находят наиболее широкое применение в системах связи, вычислительной техники и автоматизации.
Модуляцией называют процесс, при кот. электрический сигнал сообщения воздействует на колебания высокой частоты (несущие колебания) так, что их амплитуда, частота или нач. фаза изменяются во времени по тому же закону, что и напряжение сигнала сообщения. Этот процесс осущ-ся в модуляционном устройстве, на кот. одновременно поступают сигналы сообщения и колебания несущей частоты, создаваемые спец. генератором. В зависимости от того, какой из параметров несущих колебаний подвергается изменению в указанном процессе, различают: амплитудную, частотную и фазовую модуляции.
Простейшим видом модулированного сигнала является сигнал с ампли- тудной модуляцией (АМ) s(t) . Если полезный сигнал, модулирующий несу- щее колебание, представляет собой гармоническую (синусоидальную) функ- цию с частотой и амплитудой А0, изображение его амплитудного спектра
имеет вид единичной линии (рис. 4, а). Спектр результирующего сигнала
s(t) ,

 модулированного
указанным
тоном
(гармоническим
колебанием),
включает
линию
несущего
колебания
на
частоте
0
и
две
боковые
компоненты
с
рас-
стройкой
относительно
модулированного
указанным
тоном
(гармоническим
колебанием),
включает
линию
несущего
колебания
на
частоте
0
и
две
боковые
компоненты
с
рас-
стройкой
относительно
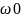 (рис.
4,
б).
Уровень
указанных
компонент
определяется
коэффициентом
амплитудной
модуляции
М,
имеет
значение
(рис.
4,
б).
Уровень
указанных
компонент
определяется
коэффициентом
амплитудной
модуляции
М,
имеет
значение
 МА0
.
МА0
.
2
 а
|S(
)|
а
|S(
)|
б |S( )|
A0 mA0
2
Ω 0 0 Ω
0 0+Ω


0
Рис. 4. Спектральное представление модулирующего гармонического сигнала (а)и модулированного сигнала с несущей частотой
(б)
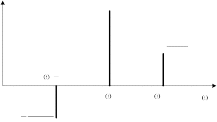
Амплитудная модуляция, в общем случае, производится сигналом, ам- плитудный спектр которого располагается в частотном интервале [ 1 , 2 ] (рис. 5). Спектр модулированного сигнала при этом содержит две боковые компоненты, расположенные зеркально относительно 0 . Форма указанных компонент повторяет огибающую спектра модулирующего сигнала.
Рис. 5. Графики амплитудного спектра модулирующего (а) и модулированного (б) сигналов
 S(
S(
0 Ω1 Ω2
 A A0
A A0
mA0
2
≈
0 Ω
mA0
2
0 0+Ω
Рис. 6. Амплитудно-частотный спектр сигнала с узкополосной частотной модуляцией

Рис. 7. Амплитудно-частотный спектр сигнала с широкополосной частотной модуляцией
Частотная модуляция. Если при амплитудной модуляции частота ω0 и начальная фаза φ несущего колебания сохраняются неизменными, а по закону передаваемого сообщения e(t) изменяется амплитуда U0, то при угловой модуляции амплитуда U0 сохраняется постоянной, а изменяться может частота либо начальная фаза несущего колебания. Поскольку частота и начальная фаза являются составляющими обобщенного угла несущего колебания [ω(t)+φ(t)], то такую модуляцию называют угловой. В зависимости от того, какой из параметров обобщенного угла, частота ω(t) или начальная фаза φ(е), несет информацию о передаваемом сообщении e(t), различают частотную либо фазовую модуляцию. При частотной модуляции амплитуда несущего колебания U0 сохраняется постоянной, а частота несущего колебания ω(t) определяется модулирующим сигналом e(t) в соответствии с выражением: ω(t) = ω0 + kЧМ e(t), где kЧМ - коэффициент пропорциональности, связывающий отклонение ΔωЧМ частоты ω(t) от своего номинального значения ω0, равное ΔωЧМ = ω(t) - ω0, и величину модулирующего напряжения e(t), вызывающего это отклонение. Максимальное отклонение частоты, вызываемое максимальным модулирующим напряжением, называют девиацией частоты. При модулирующем сигнале в виде гармонического напряжения e(t) = E cos(´Ωt+Θ) мгновенное значение частоты частотно-модулированного колебания изменяется по закону ω(t) = ω0 + kЧМ E cos(´Ωt+Θ) Временные диаграммы несущего и модулирующего колебаний, а также частотно-модулированного сигнала приведены на рисунке 8
|
Связь между спектрами модулирующего и формируемого им частотно-модулированного сигнала выражается не такими простыми выражениями, как при амплитудной модуляции, и определяется соотношением между отклонением частоты результирующего частотно-модулированного колебания, вызываемого модулирующим сигналом, и скоростью изменения этого отклонения частоты. В частности, пусть тональная модуляция гармоническим сигналом с частотой ´Ω вызывает отклонение частоты с девиацией, равной ΔωЧМ. Тогда в случае «быстрой» модуляции (при ΔωЧМ << ´Ω) полоса частот, занимаемая частотно-модулированным колебанием, определяется наибольшей частотой спектра модулирующего сигнала ПЧМ ~ 2 ´Ω. В случае «медленной» модуляции (при Δω ЧМ >> ´Ω) частотный диапазон частотно-модулированного колебания определяется величиной девиации частоты ΔωЧМ: ПЧМ ~ 2 ΔωЧМ. |
Угловая модуляция
Как уже говорилось, фазовая и частотная модуляция тесно взаимосвязаны и вместе называются угловой модуляцией. Сигнал с угловой модуляцией имеет вид колебания, начальная фаза которого зависит от времени:
sУМ(t) = A0 cos(w 0t + j (t)).
Различие между фазовой и частотной модуляцией заключается лишь в том, как именно начальная фаза j(t) связана с модулирующим сигналом.
При фазовой модуляции (ФМ) начальная фаза колебания прямо пропорциональна модулирующему сигналу:
j (t) = ksM(t).
Сам сигнал с фазовой модуляцией, таким образом, имеет вид
sФМ(t) = A0 cos(w 0t + ksM(t)).

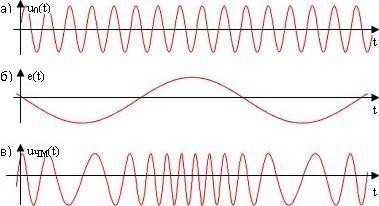 Рис.
8 Частотная модуляция:
а)
колебание с постоянной частотой; б)
модулирующий сигнал; в) частотно-модулированное
колебание
Рис.
8 Частотная модуляция:
а)
колебание с постоянной частотой; б)
модулирующий сигнал; в) частотно-модулированное
колебание