Принцип работы электрического скутера.
Скутер управляется приводом и системой контроля. В ту секунду, когда Вы ступаете на несущую платформу, пять миниатюрных гироскопических датчиков и два акселерометра улавливают изменение поверхности движения и положения Вашего тела с частотой 100 раз в секунду – это быстрее, чем может думать мозг. В нем используются специальные датчики измерения угловой скорости твердого тела, выполненные с применением кремния. Этот тип гироскопических датчиков определяет вращение тела, используя эффект Кориолиса в очень мелком масштабе. Проще говоря, эффект Кориолиса вызывает кажущееся изменение пути одного движущегося объекта по отношению к другому, вращающемуся объекту. Например, самолет, летящий по прямой траектории, кажется летящим по кривой из-за вращения Земли, находящейся под ним. В Скутере используются 2 гироскопических датчиков, хотя для работы необходимо только 1: для определения подачи Вашего тела вперед или назад , влево или вправо и для определения поворота налево или направо .Остальные датчики выполняют резервную функцию, обеспечивая большую надежность машины. Вся эта информация о положения Вашего тела и рулении, а также информация, снимаемая с сенсоров наклона, поступает в мозги устройства. Мозги и мускульная сила состоят из двух идентичных и дублирующих друг друга комплектов микропроцессорных электронных плат управления, аккумуляторных батарей и обмоток электромоторов, которые функционируют вместе и делят между собой нагрузку, создаваемую в результате приведения колес в движение. Машине необходима такая мозговая мощь, потому что ей приходится быстро производить точные настройки и корректировки, чтобы удержаться в равновесии. Если одна из плат управления (или находящиеся с ней в цепи аккумуляторная батарея, обмотка электромотора или проводка) выйдут из строя, другой комплект возьмет на себя все функции, чтобы у системы было достаточно времени для извещения пользователя о неполадке и плавной остановки.
Микропроцессоры обслуживают сложное программное обеспечение, управляющее скутером. Это программное обеспечение следит за всей информацией о состоянии равновесия, снимаемой с гироскопических датчиков, и корректирует скорость электромоторов в ответ на эту информацию. Электромоторы, питающиеся от пары литиево-йонных аккумуляторных батарей, могут вращать каждое из колес независимо от другого с переменной скоростью.
Перевернутый маятник
Перед нами плоский маятник с перемещаемой точкой опоры (рис.1.5).
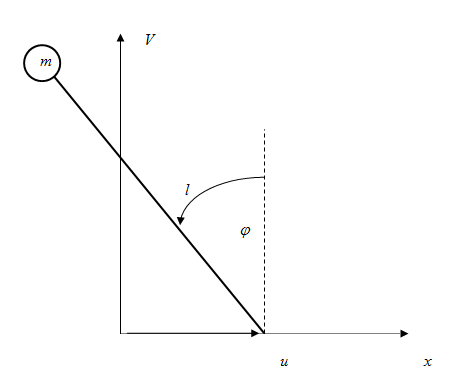
Рисунок 1.5-плоский маятник с перемещающейся точкой опоры.
- угол отклонения
маятника от вертикали;
-
горизонтальное смещение точки опоры в
плоскости качания маятника;
- длина маятника;
-
масса
Найдем функцию
Лагранжа и составим с ее помощью уравнения
движения. Непосредственно находим
координаты
,
массы
маятника
;
;
Далее находим кинетическую и потенциальную энергию.
Кинетическая
энергия – это энергия механической
системы, зависящая от скоростей движения
составляющих ее частей. В классической
механике кинетическая энергия материальной
точки массы
,
движущаяся со скоростью
,
равна:
;
; 
;
;
;
;
;
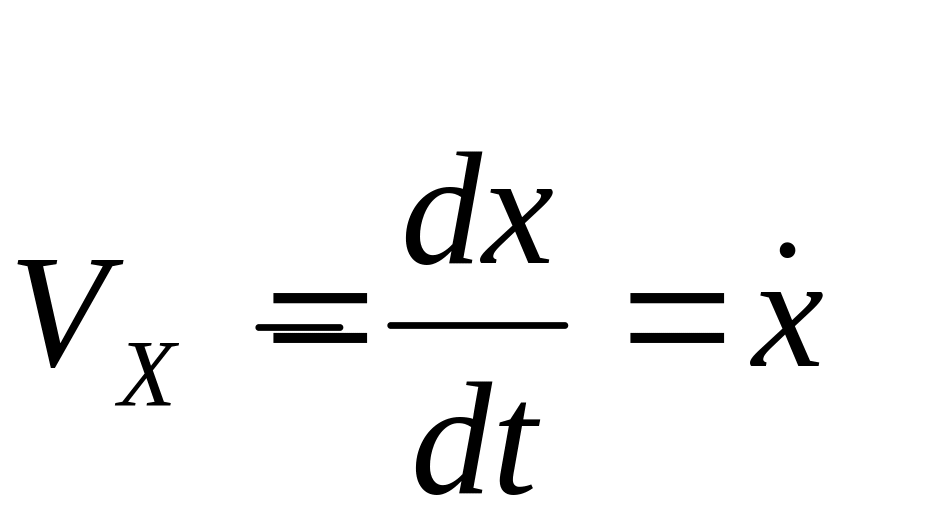Следовательно:
;
Потенциальная энергия – часть общей механической энергии системы зависящая от взаимного расположения ее частиц и от их положения во внешнем силовом поле.
;
;
;
Функция Лагранжа:
;
;
или
;
Составляем уравнение Лагранжа:
;
В рассматриваемом случае
;
;
;
И поэтому уравнение Лагранжа принимает вид
;
;
;
;
;
Ограничимся малыми углами и упростим это уравнение, записав его в виде
;
(3)
При
,
т.е. при неподвижной точке опоры маятника,
уравнение (3) переходит в хорошо нам
известное уравнение маятника,
линеаризованное вблизи верхнего
неустойчивого положения равновесия.
Это неустойчивое равновесие типа седла.
А мы хотим, чтобы оно сало устойчивым
равновесием типа узла или фокуса.
Воспользуемся возможностью выбора смещения точки опоры, возможностью управлять ее положением.
(4)
Уравнение
превратилось в уравнение осциллятора
с устойчивым положением равновесия
,
т.е чтобы маятник, стоя к верху , вел себя
также, как если бы он висел в низ и
колебания его затухали (
).
Сравнивая два уравнения(3) и (4), находим, что для этого нужно, чтобы
(5)
Реализовать
такое
можно, наблюдая за маятником и измеряя
его отклонение
и скорость отклонения
и сообщая точке опоры ускорение
согласно формуле (5).
Понятие управления объектом
Способ управления, задаваемый формулой (5), называют стратегией управления. Как уже говорилось, для её реализации нужно измерять и , и, естественно, прикладывать к точке опоры силу, которая бы сообщала точке опоры требуемое ускорение . Таким образом, для реализации управления нужна измерительная и исполнительная системы. В цирке обе эти функции с успехом выполняет жонглёр.
Итак, алгоритм решения задачи стабилизации перевернутого маятника будет следующим:
1) Записываем координаты маятника в движущейся системе отсчёта;
2) Переходим в инерциальную систему отсчёта;
3)
Дифференцируем координаты по времени,
чтобы найти
;
4) Находим ;
5) Находим кинетическую и потенциальную энергию;
6)
Пишем функцию Лагранжа
;
7) Записываем уравнение Лагранжа (уравнение колебаний) ;
8)
Находим
;
9) Результат дифференцируем по времени;
10)
Ищем производную
;
11) Подставляем всё в уравнение Лагранжа;
12) Вводим ограничение малых углов, получаем дифференциальное уравнение второго порядка;
13)
Выбираем стратегию управления в виде
,
где
,
а
;
14) Составляем определитель по системе уравнения колебаний и стратегии управления. Раскрывая определитель, анализируем полученное выражение относительно его коэффициентов, определяем при каких значениях коэффициентов равновесие будет типа фокус или узел.
Описанный процесс управления можно изобразить схемой, показанной на рис. 1.6. Схема включает объект управления – перевёрнутый маятник, на который можно воздействовать, перемещая его опору; систему измерения угла и угловой скорости ; систему управления, реализующую стратегию управления и силовое воздействие, передвигающее опору перевёрнутого маятника и сообщающее ей требуемое стратегией управления ускорение.
Принципиальная схема стабилизации стоящего вертикально вверх маятника, отображающая основной принцип управления – обратную связь.
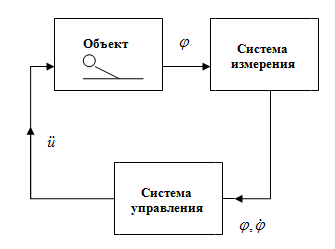
Рис. 1.6- Принципиальная схема стабилизации стоящего вертикально вверх маятника
Стратегия
управления (5) линейна по
и
,
так что
,
причём, для устойчивости требуется,
чтобы
,
а
.
При
перевёрнутый маятник также устойчив,
но его колебания возле равновесия не
затухают, так как они описываются
осциллятором (4) с
Первый
член стратегии управления
- это управление по отклонению маятника
.
Согласно этому члену, основание маятника
нужно перемещать ускоренно в ту же
сторону, что и наклон маятника, т.е. при
,а
при
.
Следующий член корректирует величину ускорения , учитывая угловую скорость вращения маятника. Если маятник движется в ту же сторону, что и его отклонение, то это приводит к увеличению необходимого ускорения по сравнению с членом , напротив, если он движется в сторону, обратную по отношению к отклонению, то это ускорение уменьшается по величине, становясь меньше .
;
Преобразуем, это уравнение так, чтобы его можно было смоделировать в MATLAB.
Делаем замену:
;
Стратегия управления:
;
-состояние
системы;
-новая
математическая модель перевернутого
маятника
В результате моделирования мы можем исследовать стабильность системы в зависимости от её параметров.
Описание обратного маятника шарнирная опора которого может ускорятся внешними воздействиями.
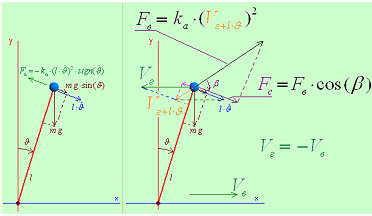
Уравнение
обратного маятника колеблющегося в
воздушной среде под действием ускорения
опоры его шарнира:
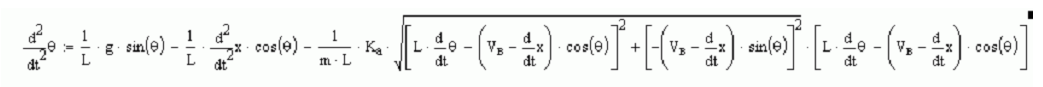
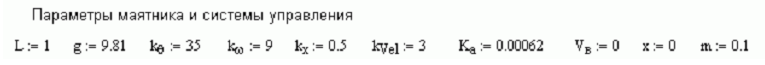Рис.
4.1.2. Формула, описывающая обратный
маятник с подвижной по горизонтали
опорой шарнира, смещение которой в
плоскости качания может управляться
внешним воздействием
Рис.
4.1.3. Система уравнений обратного маятника,
приведенная к форме Коши, что требуется
для решения задачи в Маткаде
Рис.
4.1.4. Уравнение нелинейного управления
ускорением опоры обратного маятника
для приведения его в вертикальное
положение и возвращения в начало
координат. Другими словами, это уравнение
двух, параллельно работающих ПД-регуляторов
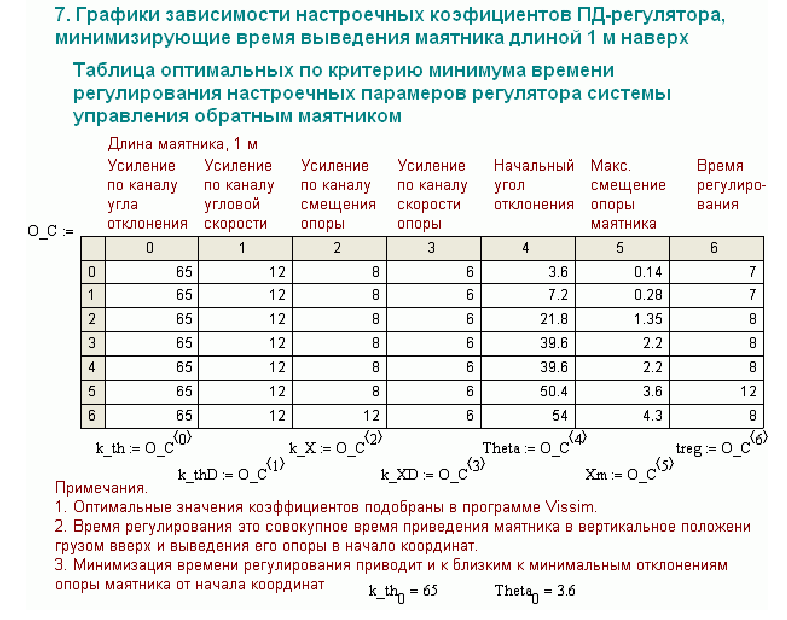
Оптимальные настроечные параметры регулятора системы выведения маятника наверх зависят от длины маятника:
