2. Стаціонарна Теплопровідность.

2.1 Теплопровідність плоского шару при відсутності внутрішніх джерел тепла з граничними умовами 1-го та 3-го роду.

Досліджуваному матеріалові надається форма тонкої круглої або квадратної пластинки. Для створення температурного перепаду по товщині пластини одна її поверхня нагрівається, а інша – охолоджується. З метою одержання одновимірного теплового потоку при виборі розмірів плоского зразка  для тіл з поганою провідністю теплоти ( Вт/(м·К)) прагнуть виконати наступну умову:

,

де d – діаметр круглої пластини (або сторона квадратної пластини).

Товщину пластини звичайно вибирають у межах від 5 до 50 мм. При цьому приймаються заходи для захисту бічної поверхні дослідного зразка і нагрівача від втрат теплоти в навколишнє середовище, особливо при високих температурах. Істотною умовою правильності визначення коефіцієнту теплопровідності є відсутність повітряних зазорів між поверхнею зразка і плоских поверхонь нагрівача і холодильника. Помилка за рахунок цього контактного опору може досягати 15 – 30% при товщині пластини 0,3 – 1,5 мм і 10 – 20% при товщині 1,5 – 3 мм. Зі збільшенням теплопровідності досліджуваного матеріалу вплив контактного теплообміну збільшується, зі збільшенням температури – зменшується через значне зростання теплообміну випромінюванням. З метою зменшення теплового опору застосовуються стискаючі пристрої, гарна обробка поверхонь як приладу , так і зразків, а також проміжні матеріали з гарною провідністю (графітові, алюмінієві, карборундові й ін. порошки).

Задача теплопровідності для однорідної плоскої пластини у випадку незалежності коефіцієнту теплопровідності від температури формулюється наступним чином:

з граничними умовами:

, ;

, .

В результаті розв’язку необхідно знайти розподіл температур в тілі і потік, що переноситься. Розв’язок в кінцевому вигляді запишеться так:

Рис.2.1 Розподіл температури в однорідній плоскій стінці

.

Маючи рівняння, що описує температурне поле, легко розрахувати тепловий потік, використовуючи закон Фур’є:

.

О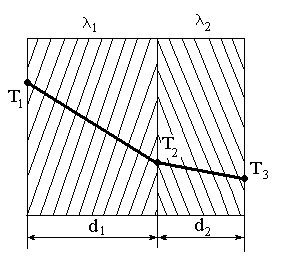 чевидно, величина q визначається не абсолютними значеннями температури, а лише їх різницею. Відношення називають термічною провідністю, а обернену величину – термічним опором . З врахуванням цього вираз для густини теплового потоку може бути записаний у вигляді:

, .

Д

Рис.2.2 Розподіл температури в багатошаровій плоскій стінці.

ля багатошарової стінки (рис. 2.2.), враховуючи, що в стаціонарному режимі величина теплового потоку, що проходить через кожний шар, не змінюється, для кожного шару можна написати:

.

Тут враховується, що контактний опір відсутній. Виключаючи невідому температуру , отримаємо

.

Отже, у випадку багатошарової стінки сумарний термічний опір є алгебраїчною сумою термічних опорів кожного шару.

У випадках, коли на границі стінки виконуються граничні умови третього роду (рис 2.3.), то вони записуються у вигляді:

, ; , .

В стаціонарному випадку тепловий потік все-таки залишається незмінним. Дійсно,

.

К

Рис.2.3 Розподіл температури при теплопередачі через плоску стінку (граничні умови 3-го роду)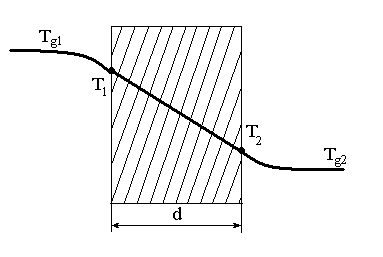

ожне з рівнянь розв’язується відносно різниці температур, які потік додаються. В результаті, густина теплового потоку прийме вигляд:

.

Величина називається термічним опором тепловіддачі. Для багатошарової стінки подібний вираз для густини теплового потоку запишеться як:

,

де – коефіцієнт теплопередачі, Вт/(м²К), і характеризує інтенсивність передачі тепла від одного нагрітого середовища до іншого. Так, як величина K менша за найменшу з величин , то для збільшення інтенсивності теплопередачі необхідно збільшити мінімальну з цих величин.