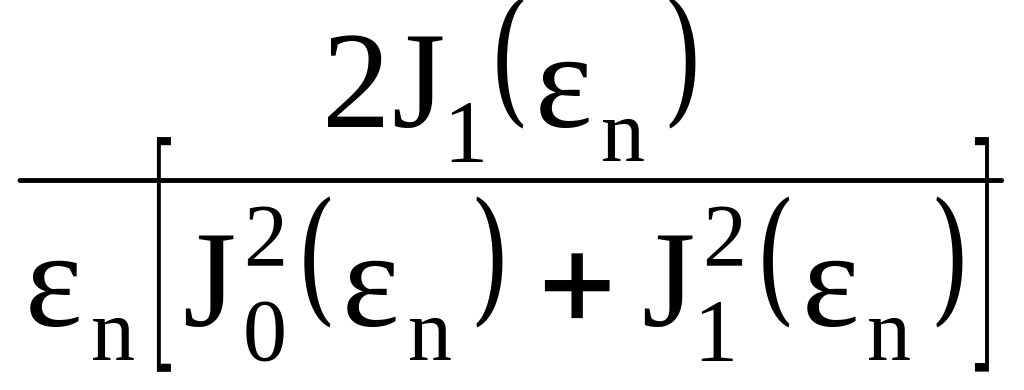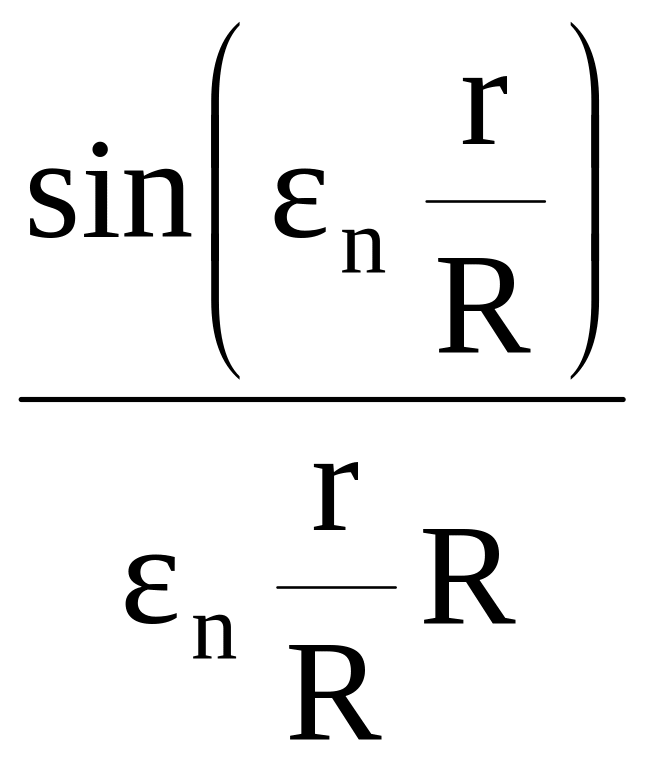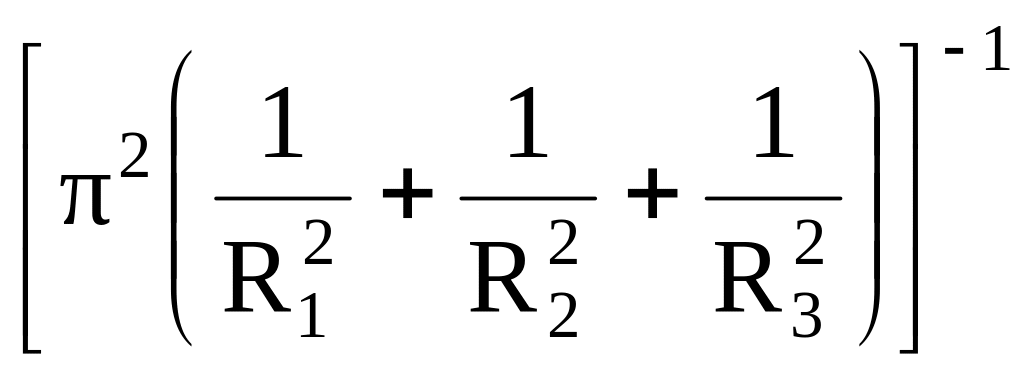- •1. Теплопровідність речовин
- •1.1. Коефіцієнт теплопровідності речовин.
- •1.2. Температурне поле. Закон Фур’є.
- •1.3. Диференційне рівняння теплопровідності для нерухомого середовища.
- •1.4. Окремі випадки диференціальних рівнянь теплопровідності. Класифікація задач теплопроводності.
- •1.5 Умови однозначності
- •2. Стаціонарна Теплопровідность.
- •2.1 Теплопровідність плоского шару при відсутності внутрішніх джерел тепла з граничними умовами 1-го та 3-го роду.
- •2.2 Теплопровідність металевого стержня з зовнішніми стоками тепла з граничними умовами 1-го та 3-го роду.
- •2.3 Одношарова стінка з внутрішніми джерелами тепла.
- •2.4 Одно- та багатошарова циліндрична стінка ( )
- •2.5 Визначення критичної товщини ізоляції трубопроводів
- •2.6 Сферична одношарова стінка з граничними умовами 1-го роду, ( )
- •2.7. Лінійна та нелінійна стаціонарна теорія теплопровідності.
- •3 Експериментальні стаціонарні методи визначення коефіцієнту теплопровідності
- •3.1. Вимірювання коефіцієнта теплопровідності діелектриків стаціонарним методом
- •3.2 Визначення коефіцієнту теплопровідності методом Хрістіансена.
- •3.3 Метод циліндрів.
- •3.4. Метод циліндричних шарів.
- •3.5. Визначення коефіцієнта теплопровідності металевого стержня (Метод Бората-Вінера)
- •3.6. Метод Кольрауша.
- •3.7. Визначення коєфіцієнту теплопровідності металів при високих температурах.
- •3.8. Вимірювання коефіцієнта теплопровідності газів
- •Розділ 4. Нестаціонарна теплопровідність
- •4.1. Класифікація процесів
- •4.2. Нагрів (охолоджування) напівобмеженого масиву. Граничні умови 1-го роду.
- •Нагрів (охолоджування) напівобмеженого масиву. Граничні умови 2-го роду.
- •1.4. Охолодження (нагрівання) необмеженої пластини
- •4.5. Охолодження (нагрів) циліндра і кулі
- •4.6. Теорема перемноження розв’язків
- •4.7 Регулярний тепловий режим
- •4.8. Періодичний нестаціонарний процес теплопровідності
- •4.9. Нестаціонарна теплопровідність при залежності теплофізичних властивостей від температури
- •Розділ 5. Експериментальні нестаціонарні методи визначення коефіцієнту теплопровідності
- •5.1 Визначення коєфіцієнту тепловіддачі методом охолодження
- •З іншого боку величину dQ можна обчислити за законом Ньютона-Ріхмана, який описує процес обміну теплом між тілом і середовищем на границі їх розподілу:
- •5.2 Вивчення теплофізичних характеристик речовини методом регулярного режиму (Метод регулярного режиму 1-го роду)
- •Література
З іншого боку величину dQ можна обчислити за законом Ньютона-Ріхмана, який описує процес обміну теплом між тілом і середовищем на границі їх розподілу:
![]() .
(5.2)
.
(5.2)
Тут – коефіцієнт теплообміну між тілом і середовищем, dS – елементарна площа поверхні тіла.
Кількість тепла, яке втрачає весь зразок, отримаємо після інтегрування (5.1) і (5.2) по всьому об’єму:
![]()
При цьому треба зважити на те, що ні похідна температури, ні теплоємність і густина речовини не залежать від розташування елементарного об’єму dV всередині тіла, так само, як і , Т, Т0 не залежать від координати елементарної поверхні dS. Тоді маємо, що:
![]()
де V і S - об’єм і площа поверхні всього тіла. Звідси ми отримуємо робочу формулу:
![]() .
(5.3)
.
(5.3)
С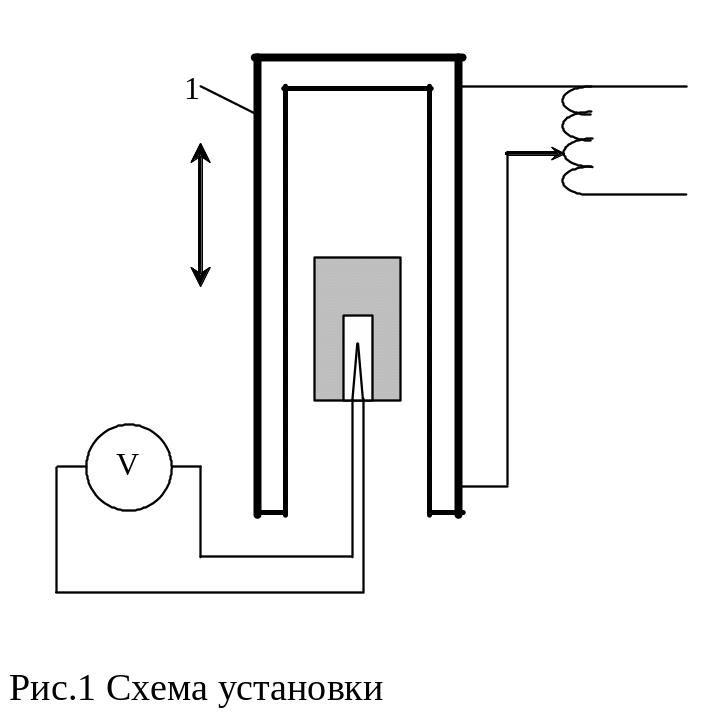 хема
експериментальної
установки приведена на рис.. Електрична
піч 1, що підключена до електричної
мережі за допомогою ЛАТру 2 може
пересуватися у вертикальному напряму.
Дослідні зразки 3 виготовлені з різних
металів уявляють з себе циліндри довжиною
30мм і діаметром 5мм з висвердленим
каналом з одного кінця. Через цей канал
всередині дослідного зразка вміщена
термопара 4, показання якої реєструються
за допомогою потенціометру 5 (ПП-63). До
потенціометру наданий спеціальний
графік перекладу його показань у значення
температури термопари.
хема
експериментальної
установки приведена на рис.. Електрична
піч 1, що підключена до електричної
мережі за допомогою ЛАТру 2 може
пересуватися у вертикальному напряму.
Дослідні зразки 3 виготовлені з різних
металів уявляють з себе циліндри довжиною
30мм і діаметром 5мм з висвердленим
каналом з одного кінця. Через цей канал
всередині дослідного зразка вміщена
термопара 4, показання якої реєструються
за допомогою потенціометру 5 (ПП-63). До
потенціометру наданий спеціальний
графік перекладу його показань у значення
температури термопари.
Дослідний
металевий зразок вводять у піч і
нагрівають до температури 500-600С,
для
цього
вмикають
піч за допомогою ЛАТру в електричну
мережу з напругою 120В.
Швидко виймають зразок з пічі і проводять
реєстрацію
температури зразка через кожні 10 секунд
знімаючи показання потенціометру.
Для більш точного визначення часової
похідної криві Т=f(t)
для всіх зразків переводять у криві
![]() .
Числові значення швидкості охолодження
отримаються шляхом розбивання залежності
Т=f(t)
на
однакові близькі один до одного ділянки
вертикальними лініями і розраховуються
як відношення значень ординат кривих
у точках де відбувається перетинання
до інтервалів часу.
.
Числові значення швидкості охолодження
отримаються шляхом розбивання залежності
Т=f(t)
на
однакові близькі один до одного ділянки
вертикальними лініями і розраховуються
як відношення значень ординат кривих
у точках де відбувається перетинання
до інтервалів часу.
5.2 Вивчення теплофізичних характеристик речовини методом регулярного режиму (Метод регулярного режиму 1-го роду)
Для тіла, що знаходиться в середовищі (рідині) температура якого не змінюється Тliq=const, а коефіцієнт теплообміну між тілом і середовищем теж є сталою величиною =const рівняння теплопровідності для тіла з температурою Т буде мати вигляд:
![]() (5.3)
(5.3)
Тут k дорівнює цілим числам, що відповідають різній симетрії задачі (1-необмежена пластина, 2-циліндр, 3-сфера).
Розв’зок рівняння (5.3) з відповідними граничними і початковими умовами, які доречі, відповідають рівномірному розподілу температури по тілу в початковий момент часу
![]()
дозволяє отримати вираз для зміни температури тіла з часом:
 (5.4)
(5.4)
де An – сталі, що визначаються з початкових умов, Un – функції координат, n – сталі, що визначаються з граничних умов, R – в залежності від k з (5.3) це або половина товщини пластини, або радіус циліндру чи сфери, а – коефіцієнт температуропроводності речовини. В таблиці 1 наведені значення величин An, Un, n, що входять до рівняння (5.4), в залежності від форми тіла. В ній використані такі позначення, як число Біо (Bi=R/) , J0 і J1 – модифіковані функції Бесселя першого роду відповідно нульового і першого порядку.
Таблиця 1 Значення коєфициентів для тіл правильної форми
Форма тіла |
An, |
Un, |
n |
, Ві |
Безмежна пластина |
|
|
|
|
Циліндр безмежної довжини |
|
|
|
2,4048 |
Сфера |
|
|
|
|
Таким чином, температурне поле в тілі залежить від його геометричної форми, початкового теплового стану та умов теплообміну тіла з навколишньою середою, і може бути подане у вигляді нескінченного ряду (5.4). Але можна показати, що цей ряд буде швидко збігатися, по закінченню терміну часу, який визначається числом Фур’є Fo0,55. Всі члени ряду стають настільки малими порівняно з першим членом, що ними можна знехтувати, і тоді розподіл температури у часі для всіх точок тіла буде мати досить простий вигляд:
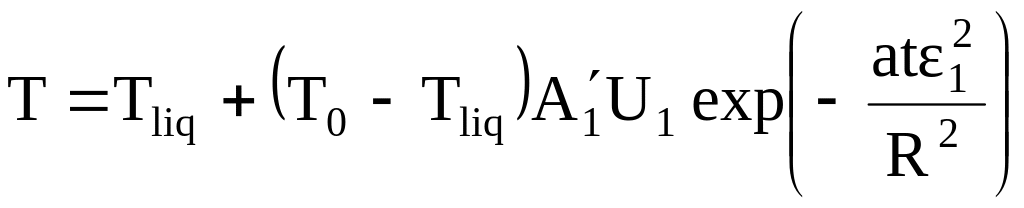
Або
![]() (5.5)
(5.5)
Тут
використані наступні позначення і
скорочення:
![]() – надлишкова температура,
– надлишкова температура,
![]() – величина, яка визначається початковим
тепловим станом тіла і не залежить від
часу, функція координат U1=U,
стала 1=,
m=a2/R2
величина
яка вимірюється в сек-1.
– величина, яка визначається початковим
тепловим станом тіла і не залежить від
часу, функція координат U1=U,
стала 1=,
m=a2/R2
величина
яка вимірюється в сек-1.
Аналіз виразу (5.5) показує, що температурне поле для тіла будь якої форми змінюється з часом за законом експоненти. Тому такий тепловий стан тіла отримав назву експоненціального регулярного режиму. А величину m, що стоїть під знаком експоненти називають темпом нагріву (охолодження) тіла.
Оскільки є функцією від Біо, то: m=f(a,,R,,K), де серед вже знайомих позначень маємо коефіцієнт K – коефіцієнт форми, відповідні значення якого наведені в таблиці 2. Інакше кажучи, темп охолодження m залежить від теплофізичних властивостей, геометричних розмірів і форми тіла, а також від умов в яких відбувається процес обміну теплом. Фізичний вміст цієї величини стає більш зрозумілим після диференціювання рівняння (5.5)
![]()
m
– характеризує відносну швидкість
змінювання температури тіла з часом. А
геометричний зміст стане явним, якщо
провести логарифмування того ж таки
рівняння (5.5):
![]() .
.
Тобто, якщо експоненціальний закон регулярного режиму подати в напівлогарифмічних координатах ln(t), то змінювання температури з часом для різних точок тіла виразиться системою паралельних прямих, кутовий коефіцієнт яких і є темпом охолодження.
Останній результат є дуже важливим для практичного способу визначення темпу охолодження за формулою:
![]()
Володіння інформацією про темп охолодження (нагріву) тіла дає можливість визначити таку важливу характеристику, як коефіцієнт температуропроводності тіла а. Для цього необхідно згадати, що m=a2/R2 . Тоді:
![]()
Основна проблема при визначенні температуропроводності а речовини полягає у тому, що є коренем трансцендентних рівнянь (див.табл.1). Але, ситуація значно спроститься, якщо розглядати граничний випадок Bi. Тоді рішення трансцендентних рівнянь є добре відомими асимптотами до яких прямує = . У відповідності до даних, що наведені в таблиці 1 отримаємо:
|
для безмежної пластини |
|
для циліндру безмежної довжини |
|
для сферичного тіла |
Вигляд цих формул, можна узагальнити шляхом введення вже згаданого вище коефіцієнту форми – K (табл.2). Маємо:
![]()
Де m - темп охолодження (нагрівання) при Bi.
Таблиця 2 Значення коефіцієнту форми для тіл правильної форми
Форма тіла |
K,м2 |
Форма тіла |
K,м2 |
Безмежна пластина |
|
Сферичне тіло |
|
Циліндр безмежної довжини |
|
Прямокутний паралелепіпед з ребрами R1, R2, R3 |
|
Циліндр довжини l |
|
- |
- |
Таким чином, коефіцієнт температуропроводності речовини визначається досить легко за формулою (8), якщо експериментально визначити темп охолодження, і коефіцієнт форми тіла – K є відомим. Але бувають випадки, коли тіло має досить складну геометричну конфігурацію, і отримати з розрахунків коефіцієнт форми тіла, а значить його температуропроводність, не уявляється можливим. Тоді його знаходять у такий спосіб: проводять експеримент із зразком складної форми, але зробленого із матеріалу з відомою температуропроводністю, після чого повторюють опит з зразком аналогічної конфігурації виготовленим з матеріалу, що підлягає дослідженню.
Наприкінці,
необхідно також визначитися з приводу
технічного забезпечення умов, дотримання
яких було визнаним обов’язковим при
отриманні вищезазначених результатів.
Виконання умови, що Bi
забезпечується використанням
охолоджувального (нагрівального)
середовища з високою т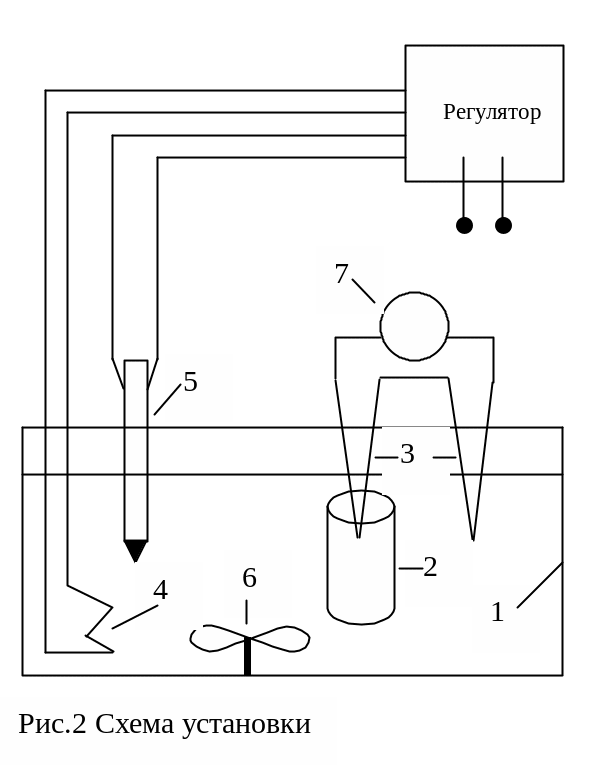 еплопровідністю
та при інтенсивному її перемішуванні.
Умова, що Тliq=const
виконується за рахунок відповідного
вибору розмірів охолоджувальної
(нагрівальної) системи – термостату
(печі). Розміри повинні бути такими, щоб
повна теплоємність системи була значно
більша у порівнянні з теплоємністю
дослідного зразку, а тепло, яким
обмінюється тіло з середовищем не
приводила до зміни температури останнього.
еплопровідністю
та при інтенсивному її перемішуванні.
Умова, що Тliq=const
виконується за рахунок відповідного
вибору розмірів охолоджувальної
(нагрівальної) системи – термостату
(печі). Розміри повинні бути такими, щоб
повна теплоємність системи була значно
більша у порівнянні з теплоємністю
дослідного зразку, а тепло, яким
обмінюється тіло з середовищем не
приводила до зміни температури останнього.
Схема експериментальної установки приведена на рис.5.2. Установка складається з термостату 1, дослідного зразка 2 правильної геометричної форми (циліндр, сферичне тіло) з різних матеріалів (ебоніт, поліметилметакрилат), диференційної термопари 3, яка вмонтована усередину дослідного зразка. Термостат обладнаний електричним нагрівачем 4 і контактним термометром 5 з регулятором, що дозволяє підтримувати температуру рідини (води) на сталому рівні (до 100С). Вода перемішується мішалкою 6, що обертається за допомогою електродвигуна. Данні вимірювання надлишкової температури фіксуються чутливим вольтметром Нагрівши воду до сталої температури, занурити у неї дослідний зразок. Провести вимірювання надлишкової температури в процесі нагрівання дослідного зразка. Для цього необхідно записати показання вольтметру, що фіксує термо-ЕРС диференційної термопари. Показання записувати через кожні 5 секунд. З графіка lnE=f(t) визначити з графіка m – темп нагрівання тіла.