4.9. Нестаціонарна теплопровідність при залежності теплофізичних властивостей від температури

У цьому розділі будуть зроблені деякі зауваження щодо можливостей розв’язку диференціального рівняння теплопровідності вигляду

. (4.68)

За умови, що , c і  залежать від температури. Така задача вельми актуальна для криогенної техніки, для якої характерна сильна і своєрідна залежність теплофізичних властивостей від температури. На відміну від рівняння стаціонарної теплопровідності, в даному випадку заміна змінної, яка б дозволила лініарізувати рівняння (4.68), неможлива. Внаслідок цього аналітичний розрахунок нестаціонарної теплопровідності у області низьких температур зустрічає значні труднощі. Для того, щоб подолати їх, на практиці широко використовують наближені методи обчислень, що включають чисельний розв’язок за допомогою ЕОМ, моделювання на аналогових обчислювальних машинах і т.п.

Проводити лінеаризацію рівняння (4.68) в області низьких температур можливо лише для випадку, коли величина коефіцієнта температуропровідності може вважатися постійною в досліджуваному діапазоні температур. Доведемо це, ввівши нову змінну

Точно таку ж, як і при розв’язуванні аналогічної задачі стаціонарної теплопровідності. Оскільки

,

З рівняння (4.68) одержимо

. (4.69)

Проведене перетворення є універсальним, в тому значенні, що воно справедливе при довільній залежності властивостей від температури.

Проте одержане рівняння (4.69), на відміну від свого стаціонарного аналога, є нелінійним, оскільки коефіцієнт температуропроводності в загальному випадку є функцією температури . В той же час для деяких матеріалів, наприклад сплавів типу неіржавіючої сталі або латуні, а також діелектриків, величина a у широкому діапазоні температур є приблизно постійною. Це стає можливим тому, що величини  і c для цих матеріалів залежать від температури однаковим чином, так що . Таким чином, рівняння (4.69) стає лінійним і для його розв’язання можуть бути використані всі методи, описані вище. Різниця полягає у тому, що тепер розв’язком служить залежність , а не , як у випадку, коли властивості не залежать від температури. Пояснимо сказане прикладом.

Нехай необхідно знайти значення температури в центрі пластини з неіржавіючої сталі товщиною , зануреної в рідкий метан з температурою T_g у момент часу . Послідовність розв’язку полягає в наступному:

1. обчислюється безрозмірний час ;

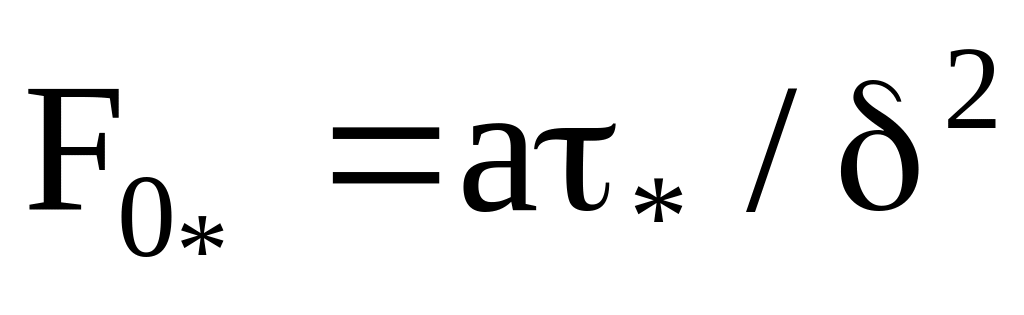2. по знайденому і заданому 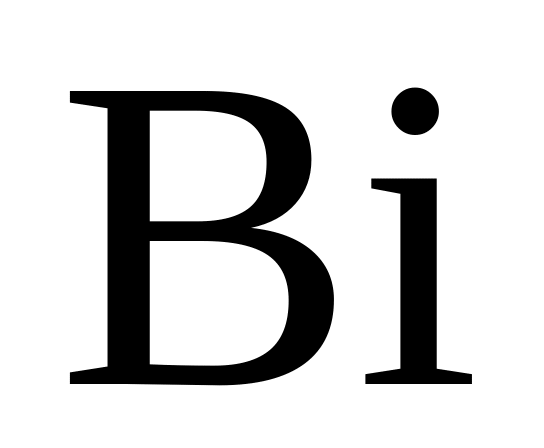за допомогою залежностей, що є в довідниковій літературі, знаходиться

;

з

Рис. 4.15. До визначення температури охолоджуючого тіла, теплофізичні властивості залежать від температури.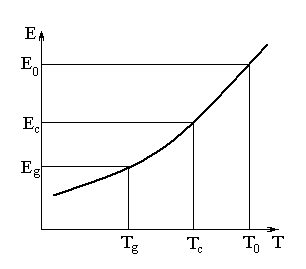

використанням залежності у аналітичній або графічній формі (рис.4.14) визначається шукана величина температуры.

Розділ 5. Експериментальні нестаціонарні методи визначення коефіцієнту теплопровідності

5.1 Визначення коєфіцієнту тепловіддачі методом охолодження

Метод охолодження передбачає, що тіло масою m яке є суцільним і однорідним спочатку нагрівають до температури Т, після чого поміщають у середовище з більш низькою температурою Т₀. Внаслідок чого температура тіла Т буде падати з часом, тобто відбувається охолодження тіла.

Кількість тепла dQ, що втрачається елементарним об’ємом dV металу за проміжок часу dt можна представити як:

(5.1)

Тут c_p – питома теплоємність речовини при сталому тиску,  - густина речовини. Знак “–” у цьому рівнянні відбиває той факт, що температура речовини зменшується. Враховуючи, що в умовах експерименту для твердого тіла його об’єм V суттєво не змінюється вважаємо у подальшому с_р=с_v=с. Крім того, для металевих тіл, які мають малі лінійні розміри – , і велику теплопровідність – , характерно . Наслідком цього буде те, що Т – температура дослідного зразка приймається однаковою в усіх точках зразка і її часткову похідну в (5.1) можна замінити на повний диференціал.