4.7 Регулярний тепловий режим

Раніше було показано, що зміна температури тіла простої геометричної форми описується єдиним рівнянням (4.44)

,

де числа утворюють дискретну зростаючу послідовність Французький дослідник Буссинеськ (1900 р.) довів, що при охолодженні будь-якого однорідного тіла як завгодно складної форми поле температур описується тим самим рівнянням. Форма рівняння вказує, що для будь-яких умов задачі завжди можна вказати такий момент часу , починаючи з якого з достатнім ступенем точності розв’язок співпадатиме з першим членом, тобто при

. (4.50)

Таким чином, момент часу розділяє дві стадії протікання процесу нагріву (охолоджування):

1) – теплові збурення лише частково проникають в тіло, є і незбурені області. Природно, що при цьому важливу роль виконує початковий розподіл температур. Ця стадія процесу носить назву неврегульованої або нерегулярної;

2) – регулярний тепловий режим. На цій стадії початкові умови виконують другорядну роль, теплові збурення охоплюють весь об'єм тіла. З (4.50) слідує рівняння

, (4.51)

що є в напівлогарифмічних координатах рівняння прямої лінії (рис. 4.12). Величина

(4.52)

одержала назву темпу охолодження. Вона є відносною швидкістю зміни температури, оскільки з (4.51) слідує, . При встановленні регулярного режиму темп охолодження не залежить ні від координати, ні від часу, а визначається геометрією тіла, його фізичними властивостями і умовами теплообміну на поверхні.

Теорія регулярного режиму була розвинена Г.М.Кондратьевим. Її найважливіші положення зводяться до наступного:

1. Т

   Рис. 4.12. Залежність безрозмірної температури від часу при охолодженні однорідного тіла.

   еорема Буссинеська справедлива також для складових і неоднорідних тіл.

2. Для однорідних тіл, коли коефіцієнт тепловіддачі – кінцева величина, темп охолодження визначається наступним співвідношенням:

, (4.53)

де – коефіцієнт нерівномірності температурного поля, що є відношенням середнього по поверхні натиску до середнього за об'ємом. Рівняння (4.53) виражає 1-у теорему Кондратьева, яка свідчить, що темп охолодження однорідного і ізотропного тіла в регулярному режимі при кінцевій величині a пропорційний коефіцієнту тепловіддачі і обернено пропорційний повній теплоємності тіла.

Рівняння (4.53) є нічим іншим, як співвідношення балансу тепла для стадії регулярного режиму. Насправді, для деякого тіла об'ємом V і з площею поверхні F

. (4.54)

Для стадії регулярного режиму , крім того, по теоремі про середнє

(4.55)

Підставляючи (4.55) в (4.54), одержимо вираз (4.53), який і потрібно було довести.

Величина коефіцієнта ψ залежить від числа , де – узагальнений характерний лінійний розмір. Очевидно, при (рис. 4.9) температура однакова в усіх точках охолоджуваного тіла, тобто і, отже, . При (рис. 4.10) надлишкова температура поверхні рівна нулю і . Цікаво, що вид функції практично не залежить від геометрії охолоджуваного тіла і може бути описаний рівнянням, запропонованим Н. А. Яришевим:

. (4.56)

3. При 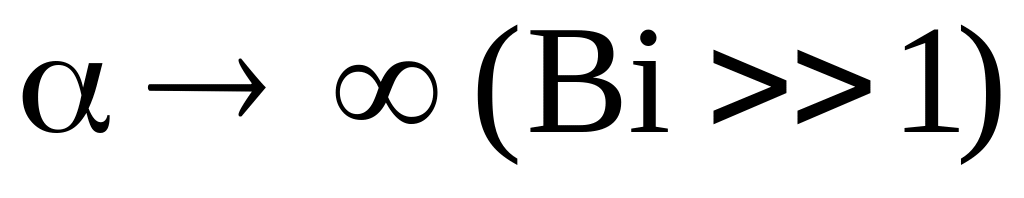темп охолоджування залишається кінцевою величиною і прагне до значення

, (4.57)

де К, м² – коефіцієнт форми – параметр, що визначається геометрією тіла; а – коефіцієнт температуропровідності.

Рівняння (4.57) носить назву 2-й теореми Кондратьева і є окремим випадком більш загального співвідношення (4.53). Для доведення запишемо умову теплообміну на границі тіла

і підставимо його в (4.53), звідки отримаємо

. (4.58)

Порівнюючи (4.57) і (4.58), можна записати

.

Очевидно, на стадії регулярного режиму цей коефіцієнт залежить тільки від геометрії системи. Якщо відомий аналітичний вираз для і (а вони легко можуть бути розраховані при ), то можна знайти відповідний коефіцієнт форми. Для тіл простої геометричної форми коефіцієнт К може бути знайдений з достатньо простих міркувань. Згідно визначенню,

,

де μ₁ – перший розв’язок характеристичного рівняння.

Для пластини при (4.4) і ;

для циліндра (перше коріння рівняння ) і ;

для сфери і .

Теорія регулярного режиму знаходить широке застосування для експериментального визначення теплофізичних властивостей речовин і дослідження тепловіддачі. Наприклад, 2-а теорема Кондратьева лежить в основі експериментального визначення коефіцієнта температуропровідності. Пристрій, що використовується в дослідах, представляє собою зразок з досліджуваного матеріалу, забезпечений пристроями для вимірювання температури, і носить назву -калориметра. На поверхні зразка, що виготовляють звичайно у вигляді сфери або циліндра, забезпечують як найбільший коефіцієнт тепловіддачі, з тим щоб виконувалася умова . При охолодженні в стадії регулярного режиму проводяться вимірювання температури і по рівнянню (4.52) визначається темп охолоджування, а потім по рівнянню (4.57) – шуканий коефіцієнт температуропровідності.

Перша теорема Кондратьева (4.53) використовується для експериментального дослідження тепловіддачі. При цьому прагнуть забезпечити умови, при яких і . Тоді, маючи в своєму розпорядженні залежність температури від часу і відомості по об'ємній теплоємності матеріалу зразка , можна знайти коефіцієнт тепловіддачі.