
- •1. Теплопровідність речовин
- •1.1. Коефіцієнт теплопровідності речовин.
- •1.2. Температурне поле. Закон Фур’є.
- •1.3. Диференційне рівняння теплопровідності для нерухомого середовища.
- •1.4. Окремі випадки диференціальних рівнянь теплопровідності. Класифікація задач теплопроводності.
- •1.5 Умови однозначності
- •2. Стаціонарна Теплопровідность.
- •2.1 Теплопровідність плоского шару при відсутності внутрішніх джерел тепла з граничними умовами 1-го та 3-го роду.
- •2.2 Теплопровідність металевого стержня з зовнішніми стоками тепла з граничними умовами 1-го та 3-го роду.
- •2.3 Одношарова стінка з внутрішніми джерелами тепла.
- •2.4 Одно- та багатошарова циліндрична стінка ( )
- •2.5 Визначення критичної товщини ізоляції трубопроводів
- •2.6 Сферична одношарова стінка з граничними умовами 1-го роду, ( )
- •2.7. Лінійна та нелінійна стаціонарна теорія теплопровідності.
- •3 Експериментальні стаціонарні методи визначення коефіцієнту теплопровідності
- •3.1. Вимірювання коефіцієнта теплопровідності діелектриків стаціонарним методом
- •3.2 Визначення коефіцієнту теплопровідності методом Хрістіансена.
- •3.3 Метод циліндрів.
- •3.4. Метод циліндричних шарів.
- •3.5. Визначення коефіцієнта теплопровідності металевого стержня (Метод Бората-Вінера)
- •3.6. Метод Кольрауша.
- •3.7. Визначення коєфіцієнту теплопровідності металів при високих температурах.
- •3.8. Вимірювання коефіцієнта теплопровідності газів
- •Розділ 4. Нестаціонарна теплопровідність
- •4.1. Класифікація процесів
- •4.2. Нагрів (охолоджування) напівобмеженого масиву. Граничні умови 1-го роду.
- •Нагрів (охолоджування) напівобмеженого масиву. Граничні умови 2-го роду.
- •1.4. Охолодження (нагрівання) необмеженої пластини
- •4.5. Охолодження (нагрів) циліндра і кулі
- •4.6. Теорема перемноження розв’язків
- •4.7 Регулярний тепловий режим
- •4.8. Періодичний нестаціонарний процес теплопровідності
- •4.9. Нестаціонарна теплопровідність при залежності теплофізичних властивостей від температури
- •Розділ 5. Експериментальні нестаціонарні методи визначення коефіцієнту теплопровідності
- •5.1 Визначення коєфіцієнту тепловіддачі методом охолодження
- •З іншого боку величину dQ можна обчислити за законом Ньютона-Ріхмана, який описує процес обміну теплом між тілом і середовищем на границі їх розподілу:
- •5.2 Вивчення теплофізичних характеристик речовини методом регулярного режиму (Метод регулярного режиму 1-го роду)
- •Література
4.5. Охолодження (нагрів) циліндра і кулі
Задачі на охолодження циліндра або кулі по своїй постановці аналогічні розглянутій вище для пластини і допускають аналітичний розв’язок. При цьому весь хід розв’язку, основаного на застосуванні методу розділення змінних, виявляється подібним. Тому обмежимося лише записом математичного формулювання задачі і її остаточного розв’язку.
Необмежений циліндр радіусом r0.
![]() .
.
початкова умова: .
граничні умови:
![]() ;
;
![]() .
.
Розв’язок має вигляд
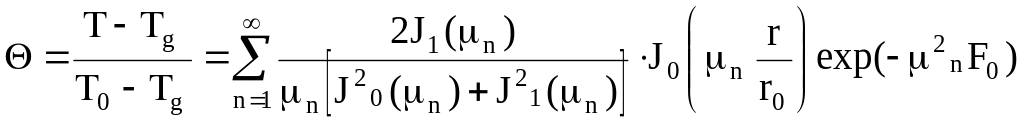 ,
(4.40)
,
(4.40)
де
![]() і
і
![]() – функції Бесселя першого роду нульового
і першого порядку;
– функції Бесселя першого роду нульового
і першого порядку;
![]() ,
μn
– розв’язки характеристичного рівняння
,
μn
– розв’язки характеристичного рівняння
![]() .
(4.41)
.
(4.41)
Куля радіусом r0
![]() .
.
Початкова
умова:
![]() .
.
граничні умови:
![]()
![]() .
.
Розв’язок має вигляд
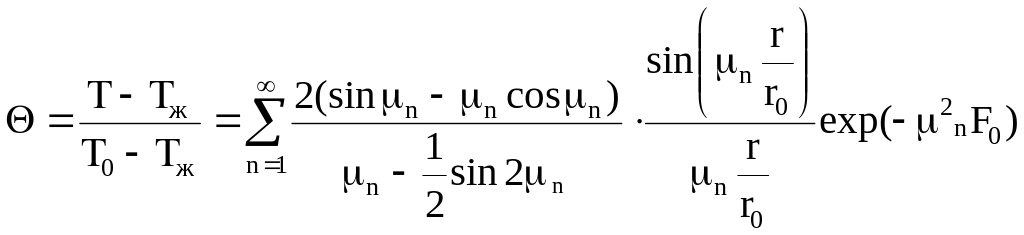 ,
(4.42)
,
(4.42)
де , μn – розв’язки характеристичного рівняння
![]() .
(4.43)
.
(4.43)
Порівнюючи (4.40) і (4.42) з (4.33), можна побачити, що для тіл простої геометричної форми структура розв’язку виявляється однаковою
![]() ,
(4.44)
,
(4.44)
де
![]() ,
,
![]() – деякі сталі коефіцієнти, що визначається
умовами однозначності (числом Біо) і
геометрією;
– деякі сталі коефіцієнти, що визначається
умовами однозначності (числом Біо) і
геометрією;
![]() –
функція координати.
–
функція координати.
Значення
і
для тіл простої геометрії, так само, як
і функції
![]() для характерних точок, розраховані і
приведені в таблицях або графічно в
довідковій літературі.
для характерних точок, розраховані і
приведені в таблицях або графічно в
довідковій літературі.
4.6. Теорема перемноження розв’язків
Очевидно, що спроби одержати строге аналітичне описання процесу охолодження тіл складнішої форми, тобто в дво- або тривимірній постановці, викликають значні труднощі. Ці труднощі до певної міри вдається усунути за допомогою теореми перемноження розв’язків, яка свідчить: безрозмірне поле температур тіла кінцевих розмірів дорівнює добутку безрозмірних температур для одновимірних тіл, перетином яких утворене дане тіло. Це, на перший погляд, неочевидне твердження легко доводиться шляхом підстановки вказаного результату в початкове математичне описання процесу і перевірки тотожності.
Н
Рис. 4.11. Охолодження циліндра
кінцевих розмірів в середовищі з
постійною температурою.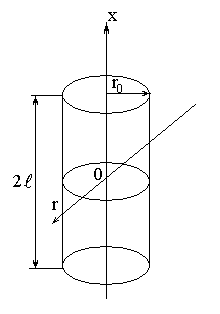
![]() .
Згідно теоремі перемноження розв’язків,
.
Згідно теоремі перемноження розв’язків,
![]() ,
(4.45)
,
(4.45)
де
![]() – розв’язок для необмеженої пластини;
– розв’язок для необмеженої пластини;
![]() – розв’язок для необмеженого циліндра.
– розв’язок для необмеженого циліндра.
Диференціальне рівняння теплопровідності для цього випадку записується так:
![]() (4.46)
(4.46)
з крайовими умовами:
![]() (4.47)
(4.47)
Розв’язок
для необмежених пластин
![]() і циліндра
відомі. Крайові умови для цих задач
виглядають таким чином:
і циліндра
відомі. Крайові умови для цих задач
виглядають таким чином:
![]() (4.48)
(4.48)
Домножаючи
лівий стовпець в (4.48) на
,
а правий – на
![]() ,
отримаємо рівняння, які співпадають з
(4.47). Далі, підставляючи
,
отримаємо рівняння, які співпадають з
(4.47). Далі, підставляючи
![]() в (4.46) і виконуючи диференціювання,
одержимо
в (4.46) і виконуючи диференціювання,
одержимо
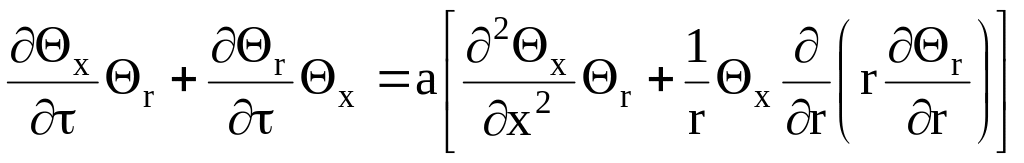 ,
,
а перегрупувавши:
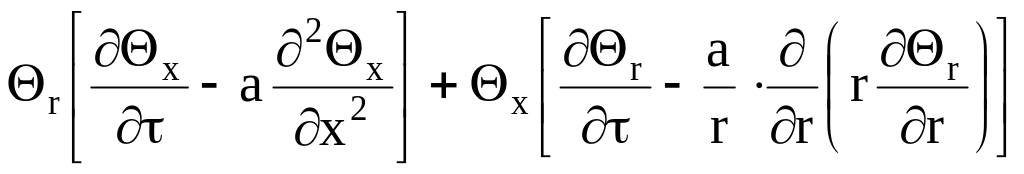 .
(4.49)
.
(4.49)
Вирази в квадратних дужках є ні що інше, як диференціальне рівняння теплопровідності для пластини і циліндра, що обертаються в нуль. В результаті (4.49) обертається в тотожність і, отже, є розв’язком поставленої задачі.
