
- •Занятие 2. «Кинематика материальной точки»
- •Занятие 3. «Кинематика материальной точки и вращательного движения»
- •Занятие 4. «Динамика материальной точки»
- •Занятие 5. «Законы сохранения импульса и энергии»
- •Занятие 6. «Законы сохранения импульса и энергии»
- •Занятие 7. «Контрольная работа №1» Занятие 8. «Гармонические колебания»
- •Занятие 9. «Затухающие колебания»
- •Занятие 10. «»
- •Занятие 11. «»
- •Занятие 12. «»
- •Занятие 13. «»
- •Занятие 14. «»
- •Занятие 15. Контрольная работа №2.
- •Занятие 16. Подготовка к зачёту.
Занятие 7. «Контрольная работа №1» Занятие 8. «Гармонические колебания»
Некоторая точка движется вдоль оси X по закону
 .
Найти: а) амплитуду и период колебаний,
изобразить график x(t);
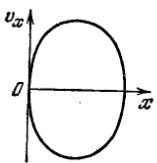
б) проекцию скорости vx
как функцию координаты x,
изобразить график vx(t).
.
Найти: а) амплитуду и период колебаний,
изобразить график x(t);
б) проекцию скорости vx
как функцию координаты x,
изобразить график vx(t).
а)
![]()
![]()
![]()
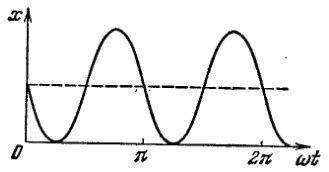
б)
![]()
![]()
![]()
![]()
Ответ:
а) ![]() ;
;
![]() ;
б)
;
б) ![]() .
.
Точка движется в плоскости Xy по закону x = A sin ωt, y = B cos ωt, где A, B, ω – постоянные. Найти: а) уравнение траектории точки y(x); б) ускорение точки в зависимости от её радиус-вектора
 относительно начала координат.
относительно начала координат.
а)
![]()
![]()



![]()
б)
![]()
![]()

Ответ:
а) ![]() ;
б)
;
б) ![]() .
.
Найти уравнение траектории y(x) точки, если она движется по закону: а) x = A sin ωt, y = A sin 2ωt; б) x = A sin ωt, y = A cos 2ωt.
а)
![]()

б)

Ответ:
а) ![]() ;
б)
;
б) ![]() .
.
Неподвижное тело, подвешенное на пружине, увеличивает её длину на Δl = 70 мм. Считая массу пружины пренебрежимо малой, найти период малых вертикальных колебаний тела.
![]()
![]()
![]()
![]()


Ответ:
![]() .
.
Частица массы m находится в однородном силовом поле, где её потенциальная энергия зависит от координаты x: U(x) = U0 (1 – cos αx), U0 и α – постоянные. Найти период малых колебаний частицы около положения равновесия.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


Ответ:
![]() .
.
То же, что и в зад. 5, но x:
 ,
α
и
b
– положительные постоянные.
,
α
и
b
– положительные постоянные.
![]()
![]()
![]()
![]()


![]()
Ответ:
![]() .
.
Найти круговую частоту и амплитуду гармонических колебаний частицы, если на расстояниях x1 и x2 от положения равновесия её скорость равна соответственно v1 и v2.
![]() ,
где x
– смещение от положения равновесия
частицы, отстоящей от источника колебаний
на расстоянии r
в направлении распространения волны;
u
– скорость распространения волны; A
– амплитуда колебаний; ω
– круговая частота.
,
где x
– смещение от положения равновесия
частицы, отстоящей от источника колебаний
на расстоянии r
в направлении распространения волны;
u
– скорость распространения волны; A
– амплитуда колебаний; ω
– круговая частота.
![]()

![]()



![]()
![]()


Подставим амплитуду в первое уравнение из системы:




Ответ:
![]() ;
;
![]() .
.
Дополнительная
задача 1.
Гармонические колебания величины s
описываются уравнением ![]() ,
м. Определите: а) амплитуду колебаний;
б) циклическую частоту; в) частоту
колебаний; г) период колебаний.
,
м. Определите: а) амплитуду колебаний;
б) циклическую частоту; в) частоту
колебаний; г) период колебаний.
![]()
а)
![]()
б)
![]()
в)
![]()
г)
![]()
Ответ:
а)
;
б)
;
в) ![]() ;
г)
;
г) ![]() .
.
Дополнительная задача 2. Материальная точка совершает гармонические колебания с амплитудой A = 4 см и периодом T = 2 с. Напишите уравнение движения точки, если её движение начинается из положения x0 = 2 см.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]() .
.
Дополнительная
задача 3.
Тело массой m
= 10 г совершает гармонические колебания
по закону ![]() ,
м. Определите максимальные значения:
а) возрастающей силы; б) кинетической
энергии.
,
м. Определите максимальные значения:
а) возрастающей силы; б) кинетической
энергии.
а)
![]()
![]()
![]()
![]()
б)
![]()
![]()

Ответ:
а) ![]() ;
б)
;
б) ![]() .
.
Занятие 9. «Затухающие колебания»
Амплитуда затухающих колебаний за время t1 = 5 мин уменьшилась в 2 раза. За какое время t2, считая от начального момента, амплитуда уменьшится в 8 раз?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]() .
.
За время t = 8 мин амплитуда затухающих колебаний маятника уменьшилась в 3 раза. Определить коэффициент затухания.
![]()
![]()
![]()
![]()
Ответ:
![]() .
.
Амплитуда колебаний маятника длиной l = 1 м за время t1 = 5 мин уменьшилась в 2 раза. Найти логарифмический декремент колебаний λ.
![]()

![]()
![]()
![]()

Ответ:
![]() .
.
Пружинный маятник (жёсткость пружины k, масса груза m) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r. Определить коэффициент затухания β и резонансную амплитуду Aрез, если амплитудное значение вынуждающей силы F0.
![]()

![]()


Ответ:
![]() ;
;
 .
.
Определить период T затухающих колебаний, если период T0 собственных колебаний системы равен 1 сек и логарифмический декремент колебаний λ = 0,628.
![]()
![]()
![]()
![]()



![]()

Ответ:
![]() .
.
Определить, на сколько резонансная частота отличается от частоты ν0 = 1 кГц собственных колебаний системы, характеризуемой коэффициентом затухания β = 400 с-1.
![]()
![]()
![]()
![]()

![]()
Ответ:
![]() .
.
Колебательная система совершает затухающие колебания с частотой ν = 1000 Гц. Определить частоту ν0 собственных колебаний, если резонансная частота νрез = 998 Гц.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Ответ:
![]() .
.
Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания λ0 = 1,5. Каким будет значение λ, если сопротивление среды увеличить в n = 2 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны?


![]()



Колебания
невозможны при ![]() ,
то есть:
,
то есть: ![]()


Ответ:
 ;
;
![]() .
.
Дополнительная задача 1. Период затухающих колебаний системы составляет 0,2 с, а отношение амплитуд первого и шестого колебаний равно 13. Определите резонансную частоту данной колебательной системы.
![]()
![]()
![]()
![]()



Ответ:
![]() .
.
Дополнительная
задача 2.
За время, в течение которого система
совершает ![]() полных колебаний, амплитуда уменьшается
в 2 раза. Определите добротность Q
системы.
полных колебаний, амплитуда уменьшается
в 2 раза. Определите добротность Q
системы.
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]() .
.
Дополнительная
задача 3.
Определите резонансную частоту
колебательной системы, если собственная
частота колебаний ![]() ,
а логарифмический декремент
,
а логарифмический декремент ![]() .
.
![]()


Ответ:
![]() .
.
