4.4.1.1 Общее постоянное резервирование

Структурная схема для общего постоянного резервирования приведена на рисунке 4.23

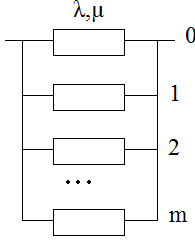
Рисунок 4.23 – Структурная схема резервированной системы

Граф состояний построен для двух случаев – восстановления с ограниченным восстановлением (одна ремонтная бригада) и неограниченным восстановлением (m+1) бригад.

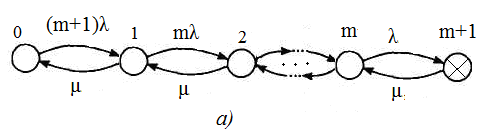
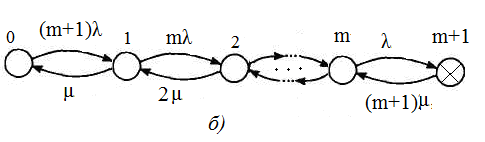
Рисунок 4.24 – Графы состояний резервированной системы: одна бригада обслуживания (а), (m+1) бригада обслуживания (б)

Введем следующие допущения:

-резервирование цельной кратности;

-последствия отказов отсутствуют.

Для случая одной обслуживающей бригады, т.е. ограниченного восстановления, интенсивность восстановления для любого состояния постоянна и равна: .

Вероятность пребывания в отказовом состоянии, т.е. коэффициент простоя:

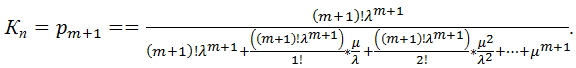(4.33)

Обозначим отношение и после сокращения числитель и знаменатель дроби на получим

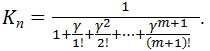(4.34)

Учитывая зависимость коэффициента готовности К_г и простоя К_п :

К_г=1-К_п, после преобразований получим

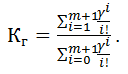(4.35)

Наработка на отказ определяется исходя из соотношения по следующей зависимости:

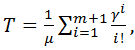(4.36)

или

(4.37)

где - наработка на отказ нерезервированной системы. Таким образом, устанавливается зависимость наработки на отказ системы от кратности резервирования.

В случае неограниченного восстановления, когда число бригад равно числу основных и резервных элементов m+1, т.е. восстановление начинается без задержки в первый момент отказа и обнаружения его. Введя соотношение получаем:

- коэффициент готовности

(4.38)

- наработка на отказ

(4.39)

- время восстановления

(4.40)

4.4.1.2 Общее резервирование замещением

Структурная схема для общего резервирования замещением приведена на рисунке 4.25. Граф состояний построен для двух случаев – восстановления с ограниченным восстановлением (одна ремонтная бригада) и неограниченным восстановлением (m+1 бригад) (рисунок 4.26).

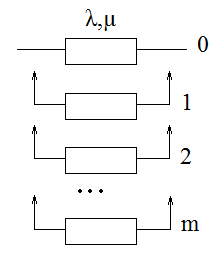
Рисунок 4.25 – Структурная схема резервированной системы

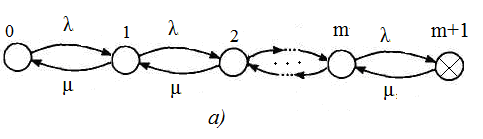
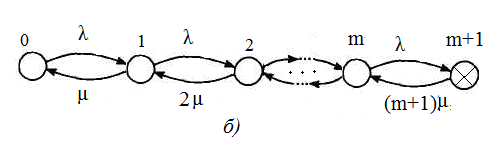
Рисунок 4.26 – Графы состояний резервированной системы: одна бригада обслуживания (а), (m+1) бригада обслуживания (б)

При одной обслуживающей бригаде коэффициент готовности определяется по следующей зависимости:

(4.41)

или

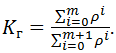(4.42)

Коэффициент готовности можно вычислить также по формуле

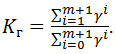(4.43)

Среднее время восстановления

(4.44)

Наработка на отказ

(4.45)

или

(4.46)

При наличии возможности неограниченного восстановления (число ремонтных бригад равно числу подсистем, т.е. m+1) коэффициент простоя К_п определяется по формуле

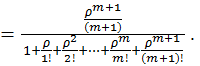(4.47)

Тогда коэффициент готовности будет иметь вид

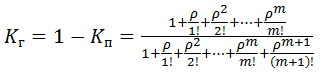(4.48)

или

(4.49)

Среднее время восстановления выражается формулой

(4.50)

Наработка на отказ вычисляется в соответствии с формулой

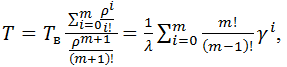(4.51)

или _,

где - наработка на отказ нерезервированной системы,